作者按

谢谢大家支持,今天一觉醒来,发现登上榜啦~~~
斐波那契数列
引入
大家都知道兔子的繁殖能力很强,这个数列的来历,大概讲的就是1对刚出生的兔子,两个月后就能够繁殖新的一对,下面红色的代表到了繁殖期,其他颜色代表未达到繁殖期,

仔细观察我们不难发现他的规律就是在第三个月开始,当月都等于前两个月之和,这个就是著名的斐波那契数列,数学上用递归来定义
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
公式

黄金分割率
天文学家开普勒发现前一项和后一项的比值趋近于一个数,就是著名的黄金分割

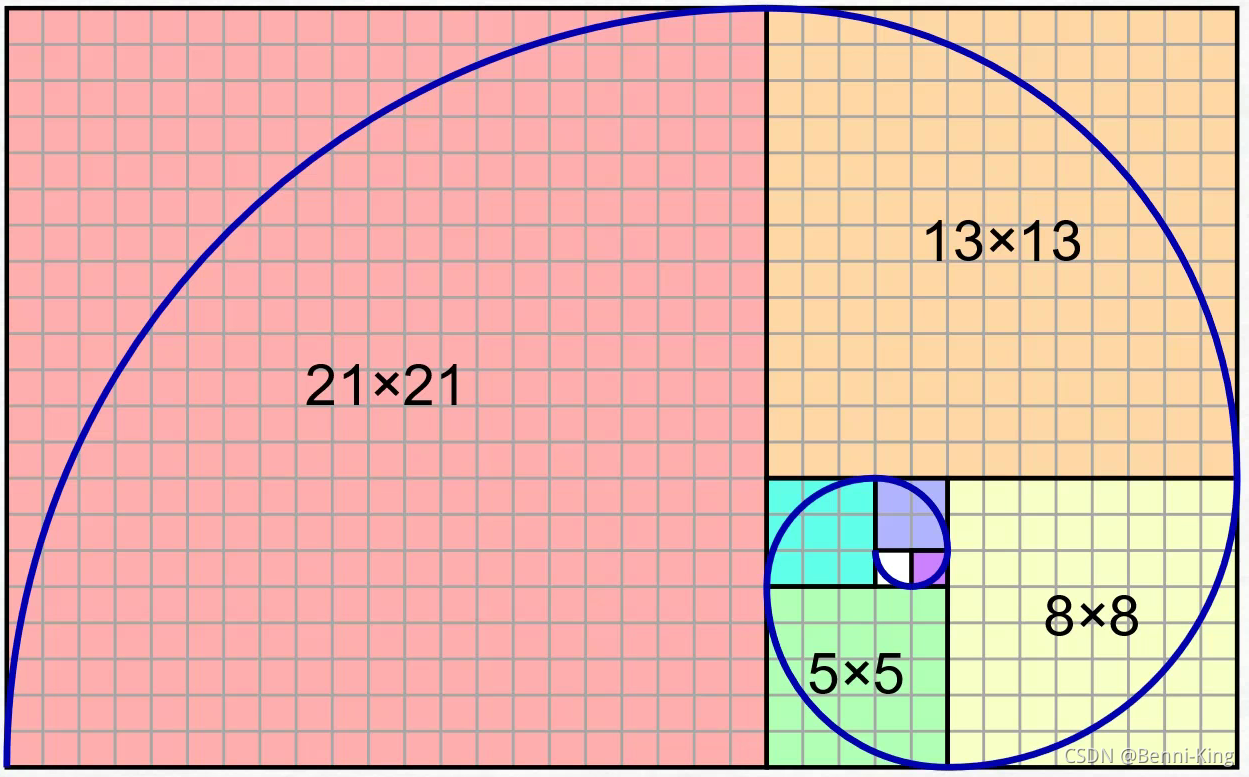
人的耳朵,海螺、向日葵的形状都近似于黄金螺旋,细菌的培养皿也是,其实很简单,如果没有天敌,营养充足,就会呈现出黄金螺旋的形状,如果后期环境恶化,这种情况就会萎缩,就像海螺最大圈停止生长一样。
递归
看到斐波那契数列的公式,发现他如果要用代码实现的话,就要用到递归,也就是函数自己调用自己,即Fn=Fn-1+Fn-2,递归一般都是按照自顶向下的形式编写
以下采用matlab代码演示
递归的斐波那契数列
大家可以思考一下,这个f入栈的形式是怎样的,也就是展示出来的f的值的大小顺序是如何
function f= fib_dg(n)
if n==1 ||n ==2
f=1;
else
f=fib_dg(n-1) + fib_dg(n-2);
end
end
阶乘
function f=jc(n)
if n==1
fprintf("现在n=%d\n",n);
f=1;
fprintf("现在f=%d\n",f);
else
fprintf("现在n=%d\n",n);
f=n.*jc(n-1);
fprintf("现在f=%d\n",f);
end
end
算法复杂度=时间复杂度+空间复杂度
如果这里的n过大,2^n就会无穷大,算法设计的就有问题,所以引出下列两种递归方法
带有备忘录的递归
不推荐用,因为麻烦
function f= fib_dg_memo(n)
global memo;
if n==1 ||n ==2
f=1;
elseif memo(n)== - 1
memo(n)=fib_dg_memo(n-1) + fib_dg_memo(n-2);
f=memo(n);
else
f=memo(n);
end
end
这个备忘录其实是-1的矩阵,然后写入的时候就把值替换掉
本期结束,下一期将展示自下而上的算法,并引出动态规划算法
























 949
949

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








