- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用
自回归图像建模
学习目标
在本课程中,我们研究了自回归图像建模,并实现了像素卷积神经网络架构。通过使用掩码卷积,我们能够应用一种卷积网络,在该网络中,一个像素仅受其所有前置像素的影响。将掩码卷积分离为水平和垂直堆叠的形式,使我们能够消除像素右上角已知的盲点问题。在实验中,自回归模型在每维度比特数方面的表现优于归一化流模型,但采样速度要慢得多。我们在此处未自行实现的改进方法包括离散逻辑斯蒂混合分布、下采样架构以及以对角线方式改变像素顺序。
相关知识点
- 掩码自回归卷积
- 门控像素卷积神经网络与采样
学习内容
在本课程中,我们将为图像建模任务实现一个自回归似然模型。自回归模型是一类天然强大的生成模型,不仅构成了当前基于似然的图像建模领域的最先进架构之一,也是诸如GPT3等大型语言生成模型的基础。与语言生成类似,自回归模型在图像上的工作原理是:基于所有先前像素来建模某个像素的似然。例如,在下图中,我们将像素 建模为基于所有先前(图中蓝色)像素的条件概率分布:
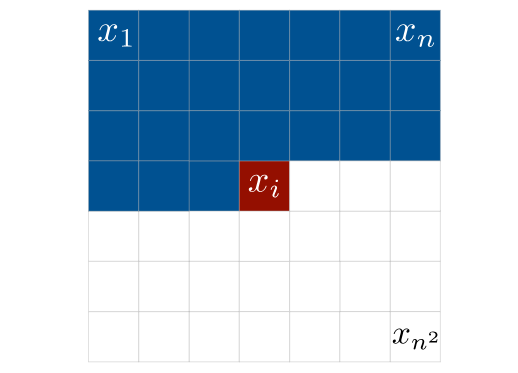
一般来说,针对高维数据 x \mathbf{x} x的自回归模型会将联合分布分解为以下条件分布的乘积:
p ( x ) = p ( x 1 , . . . , x n ) = ∏ i = 1 n p ( x i ∣ x 1 , . . . , x i − 1 ) p(\mathbf{x})=p(x_1, ..., x_n)=\prod_{i=1}^{n} p(x_i|x_1,...,x_{i-1}) p(x)=p(x1,...,xn)=i=1∏np(xi∣x1,...,xi−1)
学习这些条件分布通常比直接学习联合分布 p ( x ) p(\mathbf{x}) p(x) 容易得多。然而,自回归模型的缺点包括采样速度慢——尤其是对于大尺寸图像,因为我们需要让模型进行“高度×宽度”次前向传播。此外,对于某些应用场景,我们需要如变分自动编码器(VAEs)和归一化流(Normalizing Flows)中所建模的隐空间。例如,在自回归模型中,由于缺乏隐表示,我们无法在两张图像之间进行插值。我们将在实现过程中探讨并讨论这些优缺点。
我们的实现将聚焦于 PixelCNN 模型。当前大多数最先进(SOTA)模型都将 PixelCNN 作为其基础架构,并且已有各种改进性能的扩展方案(例如:PixelCNN++ 和 PixelSNAIL)。因此,实现 PixelCNN 是我们这个实验的良好起点。
1 掩码自回归卷积
1.1 环境准备
%pip install seaborn
%pip install pytorch_lightning
# 导入库
import os
import math
import torch
import torch_npu
import numpy as np
# 绘图相关库导入
import matplotlib.pyplot as plt
plt.set_cmap('cividis')
%matplotlib inline
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf') # 用于导出
from matplotlib.colors import to_rgb
import seaborn as sns
# 进度条
from tqdm import tqdm
# PyTorch相关库
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import torch.optim as optim
# Torchvision相关库
import torchvision
from torchvision.datasets import MNIST
from torchvision import transforms
# 导入PyTorch Lightning相关库
import pytorch_lightning as pl
from pytorch_lightning.callbacks import LearningRateMonitor, ModelCheckpoint
# 数据集所在文件夹路径
DATASET_PATH = "./data"
# 预训练模型保存的文件夹路径
CHECKPOINT_PATH = "./saved_models/tutorial12"
# 设置随机种子
pl.seed_everything(42)
# 指定设备。
device = torch.device("npu")
print("Using device", device)
1.2 加载数据集
- 获取数据集并解压
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/dcb5671a2d4011f08d8ffa163edcddae/MNIST_DATA.tar.gz
!tar -zxvf MNIST_DATA.tar.gz
- 本课程将使用 MNIST 数据集,并且每个像素采用 8 位表示(取值范围在 0 到 255 之间)。下面是加载该数据集的操作:
# 将图像从 0-1 的范围转换为 0-255 的范围(整数)。我们使用长整型数据类型,因为后续也会将这些图像用作标签。
def discretize(sample):
return (sample * 255).to(torch.long)
# 对每张图像应用的变换操作 => 仅将它们转换为张量
transform = transforms.Compose([transforms.ToTensor(),
discretize])
# 加载训练数据集。我们需要将其划分为训练集和验证集两部分。
train_dataset = MNIST(root=DATASET_PATH, train=True, transform=transform, download=False)
pl.seed_everything(42)
train_set, val_set = torch.utils.data.random_split(train_dataset, [50000, 10000])
# 加载测试集
test_set = MNIST(root=DATASET_PATH, train=False, transform=transform, download=False)
# 我们定义一组数据加载器,以便后续能用于不同目的。
train_loader = data.DataLoader(train_set, batch_size=128, shuffle=True, drop_last=True, pin_memory=True, num_workers=4)
val_loader = data.DataLoader(val_set, batch_size=128, shuffle=False, drop_last=False, num_workers=4)
test_loader = data.DataLoader(test_set, batch_size=128, shuffle=False, drop_last=False, num_workers=4)
- 对一些数据示例进行可视化,以便直观地了解数据情况:
def show_imgs(imgs):
num_imgs = imgs.shape[0] if isinstance(imgs, torch.Tensor) else len(imgs)
nrow = min(num_imgs, 4)
ncol = int(math.ceil(num_imgs/nrow))
imgs = torchvision.utils.make_grid(imgs, nrow=nrow, pad_value=128)
imgs = imgs.clamp(min=0, max=255)
np_imgs = imgs.cpu().numpy()
plt.figure(figsize=(1.5*nrow, 1.5*ncol))
plt.imshow(np.transpose(np_imgs, (1,2,0)), interpolation='nearest')
plt.axis('off')
plt.show()
plt.close()
show_imgs([train_set[i][0] for i in range(8)])

1.3 掩码卷积
PixelCNN 的核心模块是其掩码卷积。与语言模型不同,我们不会对每个像素逐个应用长短期记忆网络(LSTM)。因为图像是网格状结构而非序列,这样做效率会很低。因此,更好的方法是依靠在深度卷积神经网络(CNN)分类模型中已取得成功的卷积操作。
当然,这里我们不能直接应用标准卷积。请记住,在自回归模型的训练过程中,我们希望使用 teacher forcing,这既有助于模型训练,又能显著减少训练所需的时间。对于图像建模,teacher forcing 是通过将训练图像作为模型的输入来实现的。因此,我们需要确保对特定像素的预测只能受其前驱像素的影响,而不能受其自身的值或任何 “后续” 像素的影响。为此,我们应用带掩码的卷积。
我们使用哪种掩码取决于我们所确定的像素顺序,也就是说,我们首先预测的是哪个像素,其次预测的是哪个像素,诸如此类。最常用的排序方式是将左上角的像素指定为起始像素,并逐行对像素进行排序。因此,第二个像素位于第一个像素的右侧(第一行,第二列),一旦到达该行的末尾,我们就从第二行的第一列开始。
如果我们现在想将此应用于我们的卷积操作,我们需要确保像素 1 的预测不受其自身 “真实” 输入以及其右侧和下方任何行中所有像素的影响。在卷积中,这意味着我们要将权重矩阵中考虑右侧和下方像素的那些元素设置为零。以一个 5×5 的卷积核为例,掩码如下图所示:
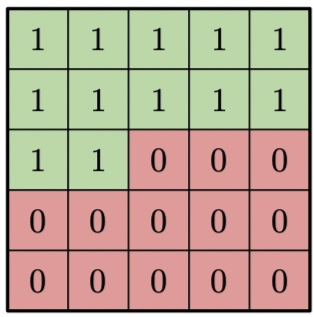
图1 掩码示意图
在深入研究掩码卷积在像素卷积神经网络(PixelCNN)中的具体应用之前,我们先来编写一个模块,该模块能让我们对卷积操作应用任意掩码。
class MaskedConvolution(nn.Module):
def __init__(self, c_in, c_out, mask, **kwargs):
"""
实现一个对其权重应用了掩码的卷积操作。
输入:
c_in - 输入通道的数量
c_out - 输出通道的数量
mask - 形状为 `[kernel_size_H, kernel_size_W]` 的张量,其中卷积需要被掩码的位置为 0,其他位置为 1。
kwargs - 卷积操作的额外参数
"""
super().__init__()
# 为了简化操作:自动计算填充量
kernel_size = (mask.shape[0], mask.shape[1])
dilation = 1 if "dilation" not in kwargs else kwargs["dilation"]
padding = tuple([dilation*(kernel_size[i]-1)//2 for i in range(2)])
# 实际的卷积操作
self.conv = nn.Conv2d(c_in, c_out, kernel_size, padding=padding, **kwargs)
# 将掩码作为缓冲区 => 它不是参数,但仍是模块的一个张量
# (必须随设备一起移动)
self.register_buffer('mask', mask[None,None])
def forward(self, x):
self.conv.weight.data *= self.mask # 确保在掩码位置处的值为零
return self.conv(x)
1.4 垂直和水平卷积堆叠
为了构建我们自己的自回归图像模型,我们只需将几个掩码卷积相互堆叠起来即可。
当依次应用几个掩码卷积时,一个像素的感受野在右上方会出现一个 “盲区”,如下图所示:
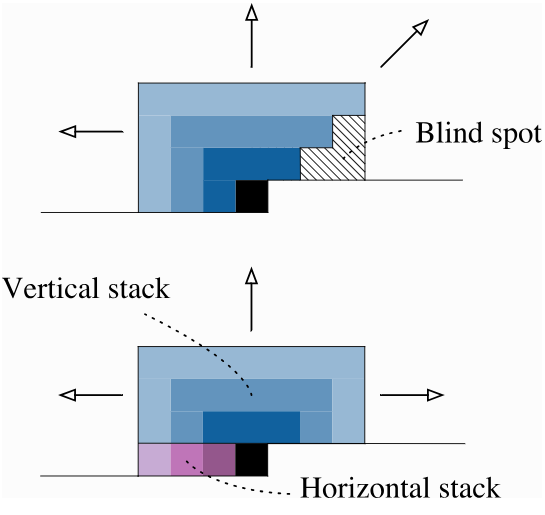
图2 掩码卷积“盲区”示意图
尽管一个像素应该能够考虑到它上方和左方的所有其他像素,但一堆掩码卷积却不允许我们观察到右上方的像素。这是因为我们用于卷积的上方像素的特征并不包含同一行右方像素的任何信息。为了克服这个问题,我们将卷积拆分为垂直卷积堆叠和水平卷积堆叠。垂直堆叠会考虑当前像素上方的所有像素,而水平堆叠则会考虑左方的所有像素。在将它们两者分开的情况下,我们实际上可以通过垂直堆叠来观察右方的像素,同时又不会违背我们的任何假设。这两种卷积也在上图中展示了出来。
根据上述说明,编写模块:
class VerticalStackConvolution(MaskedConvolution):
def __init__(self, c_in, c_out, kernel_size=3, mask_center=False, **kwargs):
# 屏蔽掉下方的所有像素。为了提升效率,我们也可以减小卷积核在高度方向上的尺寸,但为求简便,我们在此还是采用掩码的方式。
mask = torch.ones(kernel_size, kernel_size)
mask[kernel_size//2+1:,:] = 0
# 对于第一个卷积层,我们还将对中心行进行掩码处理。
if mask_center:
mask[kernel_size//2,:] = 0
super().__init__(c_in, c_out, mask, **kwargs)
class HorizontalStackConvolution(MaskedConvolution):
def __init__(self, c_in, c_out, kernel_size=3, mask_center=False, **kwargs):
# 屏蔽掉左侧的所有像素。请注意,我们的卷积核在高度上的尺寸为 1,因为我们只关注同一行的像素。
mask = torch.ones(1,kernel_size)
mask[0,kernel_size//2+1:] = 0
# 对于第一个卷积操作,我们还会对中心像素进行掩码处理。
if mask_center:
mask[0,kernel_size//2] = 0
super().__init__(c_in, c_out, mask, **kwargs)
请注意,我们有一个名为 mask_center 的输入参数。要记住,模型的输入是实际的输入图像。因此,我们应用的第一个卷积不能将中心像素用作输入,而必须进行掩码处理。然而,所有后续的卷积都应该使用中心像素,因为否则我们就会丢失上一层的特征。所以,对于第一个卷积来说,输入参数 mask_center 的值为 True,而对于其他所有卷积,该参数的值为 False。
1.5 可视化感受野
为了验证我们对掩码卷积的实现效果,我们可以将通过这些掩码卷积得到的感受野可视化。
随着卷积层数量的增加,感受野在垂直和水平方向上都会扩大,并且不会出现盲区的问题。
感受野可以通过经验方法来测量,即针对特定像素的输出特征,将关于输入的任意损失进行反向传播。
我们在下面实现这一想法,并在下方对感受野进行可视化呈现。
让我们首先可视化一个没有中心像素的水平卷积的感受野。我们使用一张较小的、任意的输入图像(11×11 像素),并计算中心像素的损失。为了简便起见,我们将所有权重初始化为 1,将偏置初始化为 0,并且使用单通道。
inp_img = torch.zeros(1, 1, 11, 11)
inp_img.requires_grad_()
def show_center_recep_field(img, out):
"""
计算输入相对于输出中心像素的梯度,并将整体感受野可视化。
输入:
img - 我们想要计算其感受野的输入图像。
out - 用于反向传播的输出特征/损失,它应该是网络/计算图的输出。
"""
# 确定梯度
loss = out[0,:,img.shape[2]//2,img.shape[3]//2].sum() # 为简便起见,采用 L1 损失函数。
loss.backward(retain_graph=True) # 保留计算图,因为我们希望堆叠多个层并展示所有层的感受野。
img_grads = img.grad.abs()
img.grad.fill_(0) # 重置梯度
# 绘制感受野
img = img_grads.squeeze().cpu().numpy()
fig, ax = plt.subplots(1,2)
pos = ax[0].imshow(img)
ax[1].imshow(img>0)
# 如果中心像素没有任何梯度(对于标准自回归模型来说应该是这种情况),则将其标记为红色。
show_center = (img[img.shape[0]//2,img.shape[1]//2] == 0)
if show_center:
center_pixel = np.zeros(img.shape + (4,))
center_pixel[center_pixel.shape[0]//2,center_pixel.shape[1]//2,:] = np.array([1.0, 0.0, 0.0, 1.0])
for i in range(2):
ax[i].axis('off')
if show_center:
ax[i].imshow(center_pixel)
ax[0].set_title("Weighted Receptive Field")
ax[1].set_title("Binary Receptive Field")
plt.show()
plt.close()
show_center_recep_field(inp_img, inp_img)

感受野以黄色显示,中心像素以红色显示,感受野之外的所有其他像素为深蓝色。正如预期的那样,一个中心像素被掩码且使用 3 × 3 3\times3 3×3 卷积核的单个水平卷积的感受野仅为左侧的像素。如果我们使用更大的卷积核尺寸,那么左侧会有更多的像素被纳入考虑范围。
horiz_conv = HorizontalStackConvolution(c_in=1, c_out=1, kernel_size=3, mask_center=True)
horiz_conv.conv.weight.data.fill_(1)
horiz_conv.conv.bias.data.fill_(0)
horiz_img = horiz_conv(inp_img)
show_center_recep_field(inp_img, horiz_img)
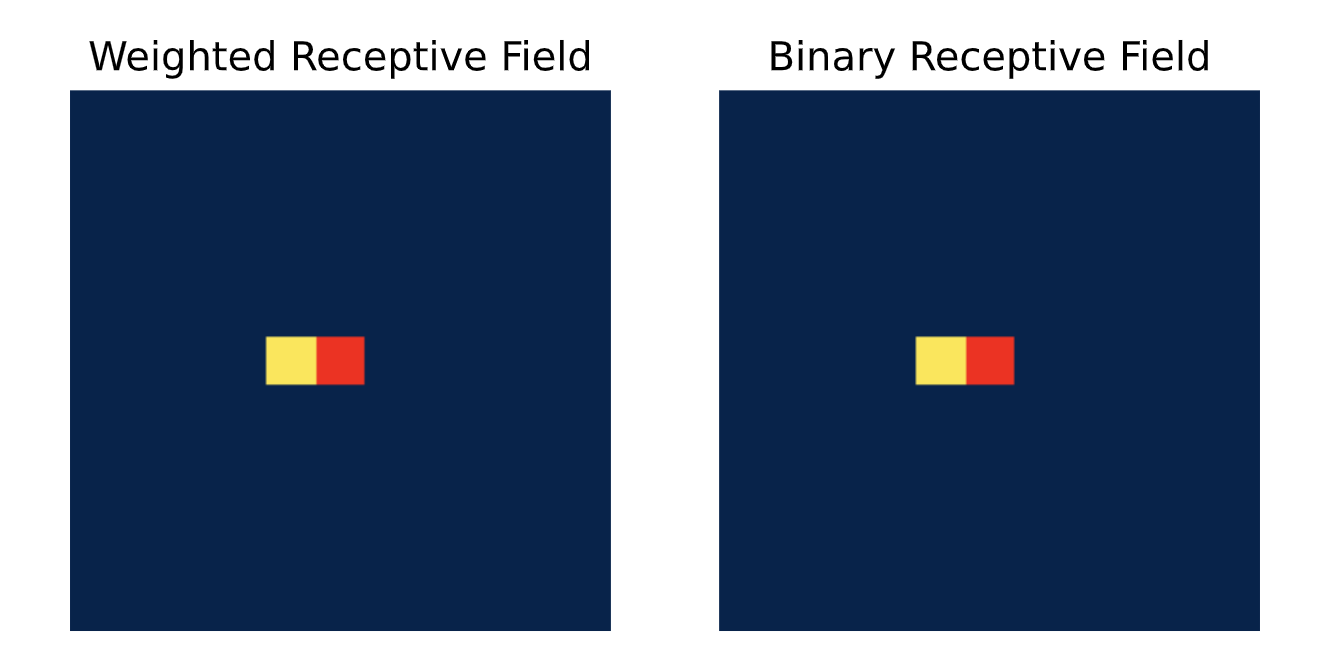
接下来,让我们看一下垂直卷积:
vert_conv = VerticalStackConvolution(c_in=1, c_out=1, kernel_size=3, mask_center=True)
vert_conv.conv.weight.data.fill_(1)
vert_conv.conv.bias.data.fill_(0)
vert_img = vert_conv(inp_img)
show_center_recep_field(inp_img, vert_img)
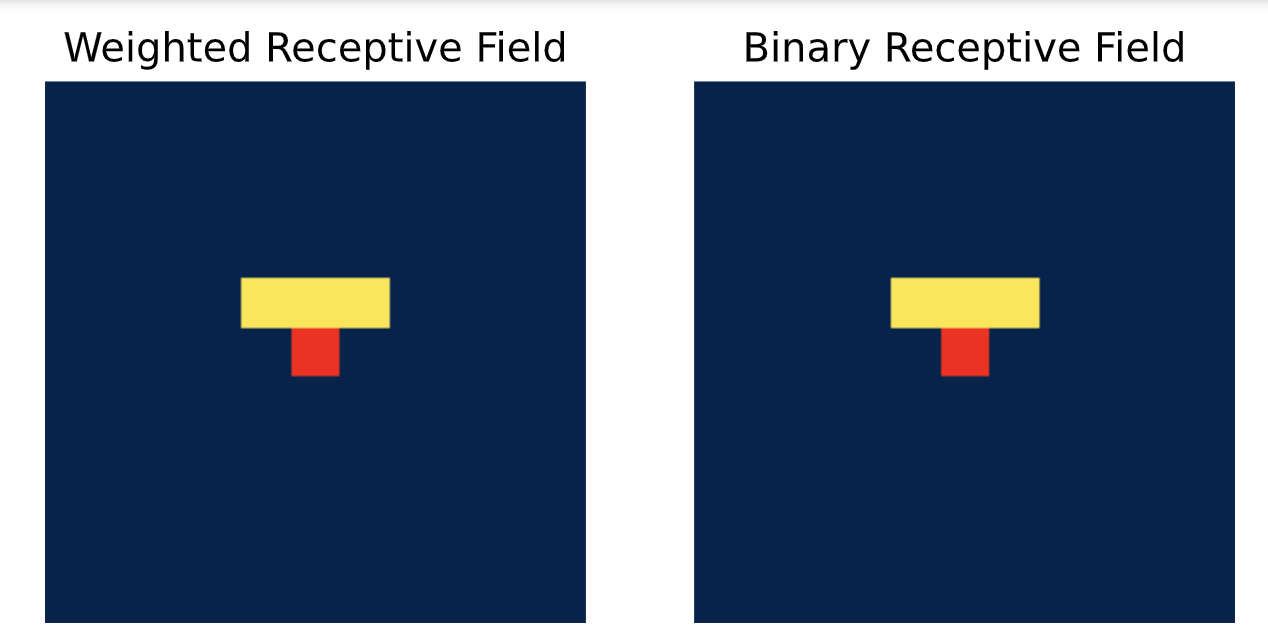
垂直卷积会考虑上方的所有像素。将这两种情况结合起来,我们就能得到原始掩码卷积的“L”形感受野:
horiz_img = vert_img + horiz_img
show_center_recep_field(inp_img, horiz_img)
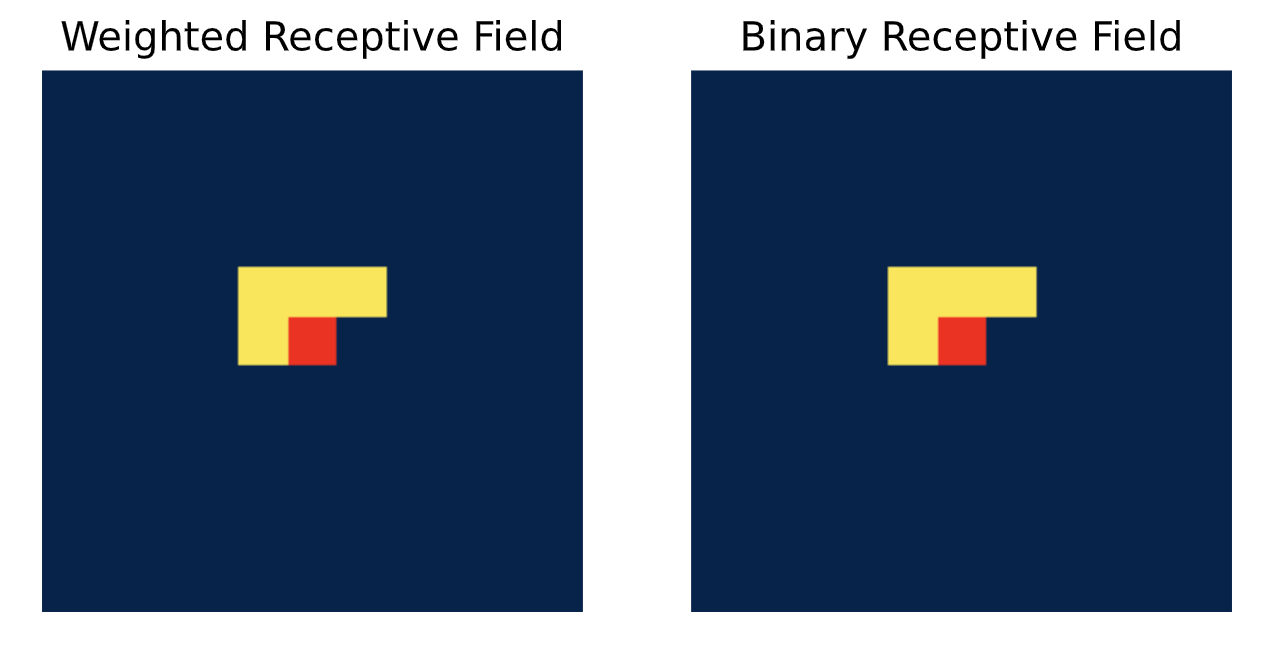
如果我们堆叠多个水平和垂直卷积层,需要考虑两个方面:
- 在后续的卷积操作中,不应再对中心像素进行掩码处理,因为该像素位置的特征已经与其实际值无关。如果难以理解为何可以这样做,只需将下面的值改为
mask_center=True,看看会发生什么。 - 垂直卷积不能处理水平卷积得到的特征。在水平卷积的特征图中,一个像素包含了其左侧所有“真实”像素的信息。如果我们应用一个还会利用右侧特征的垂直卷积,实际上就会将感受野扩展到真实输入,而这是我们要避免的。因此,特征图只能在水平卷积时进行合并。
基于此,我们可以按以下方式堆叠卷积层。我们有两个特征流:一个用于垂直卷积堆叠,另一个用于水平卷积堆叠。水平卷积可以处理之前水平和垂直卷积的联合特征,而垂直卷积堆叠仅将其自身之前的特征作为输入。为了快速实现,我们可以在每一层将水平和垂直卷积的输出特征相加,并将这些相加后的特征作为最终输出特征来计算损失。下面展示了一个连续四层卷积的实现。请注意,我们复用了上面提到的 mask_center=True 时其他卷积得到的特征。
下面展示的是水平卷积堆叠的感受野可视化结果,其中包含了垂直卷积的特征。与之前不同,它在各层不断扩大且没有任何盲点。“加权”感受野和“二值”感受野的区别在于,对于后者,我们只需检查是否有梯度反向传播到该像素,这表明中心像素确实能够利用该像素的信息。然而,由于卷积核的权重设置,某些像素对预测结果的影响会比其他像素更强。在加权感受野可视化中,我们通过绘制每个像素的梯度幅值而非简单的二值“是/否”来呈现这种差异。
# 以对所有输入像素赋予相同权重的方式初始化卷积层
horiz_conv = HorizontalStackConvolution(c_in=1, c_out=1, kernel_size=3, mask_center=False)
horiz_conv.conv.weight.data.fill_(1)
horiz_conv.conv.bias.data.fill_(0)
vert_conv = VerticalStackConvolution(c_in=1, c_out=1, kernel_size=3,mask_center=False)
vert_conv.conv.weight.data.fill_(1)
vert_conv.conv.bias.data.fill_(0)
# 在这里,我们将卷积层用于这 4 层。
# 请注意,在标准网络中,我们不会这样做,而是学习 4 个独立的卷积层。
# 由于此代码单元仅用于可视化目的,所以我们在所有层中复用这些卷积层。
for l_idx in range(4):
vert_img = vert_conv(vert_img)
horiz_img = horiz_conv(horiz_img) + vert_img
print(f"Layer {l_idx+2}")
show_center_recep_field(inp_img, horiz_img)
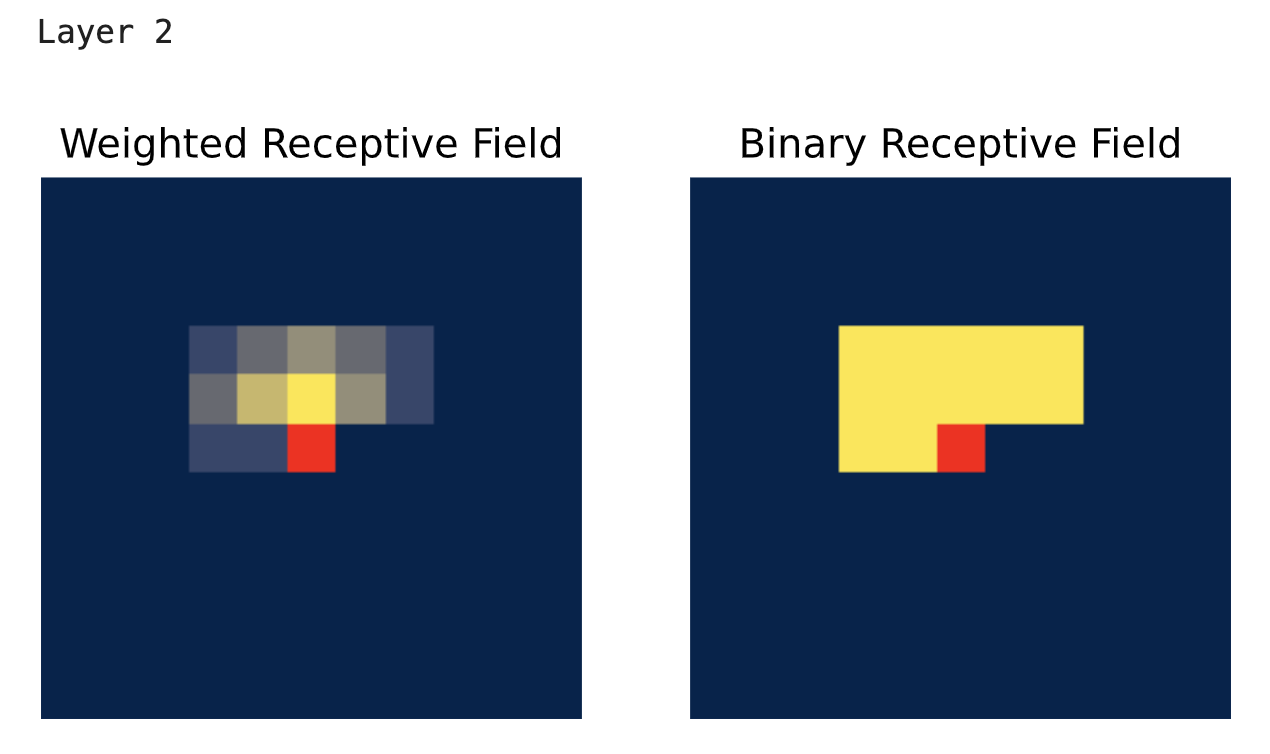
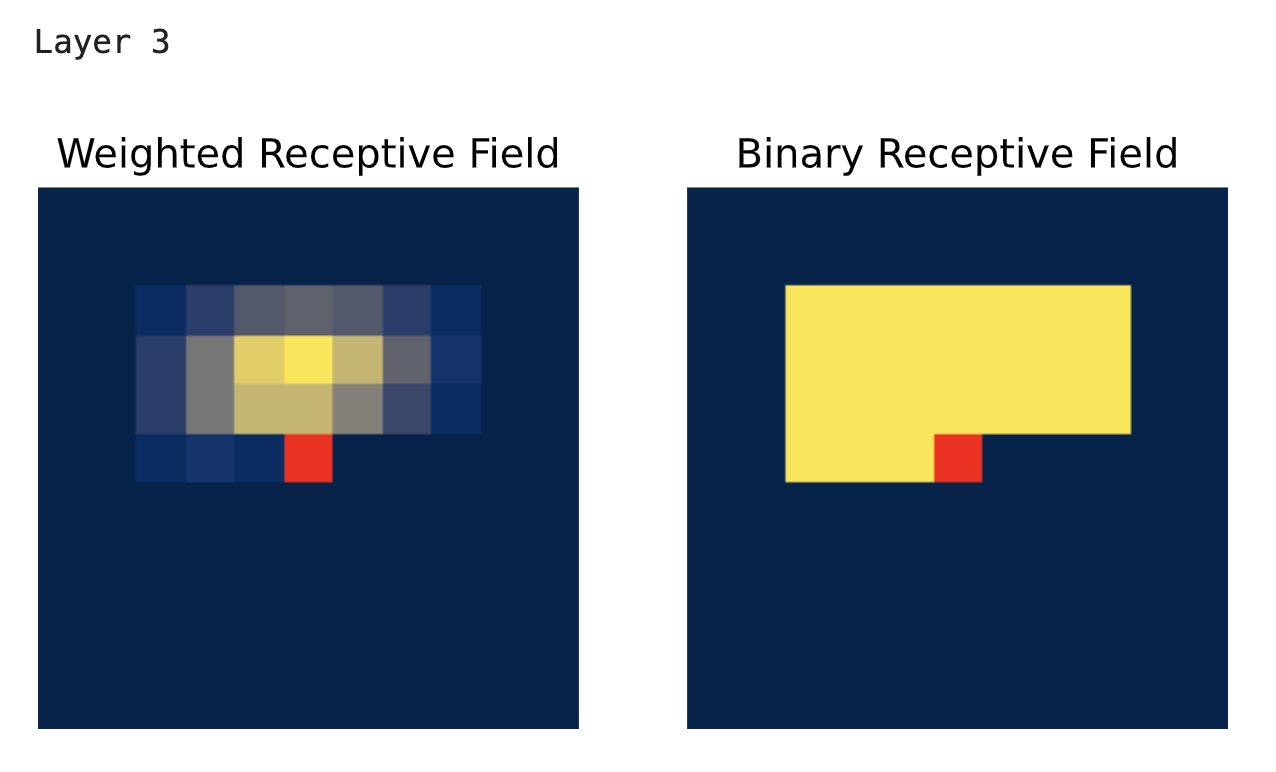
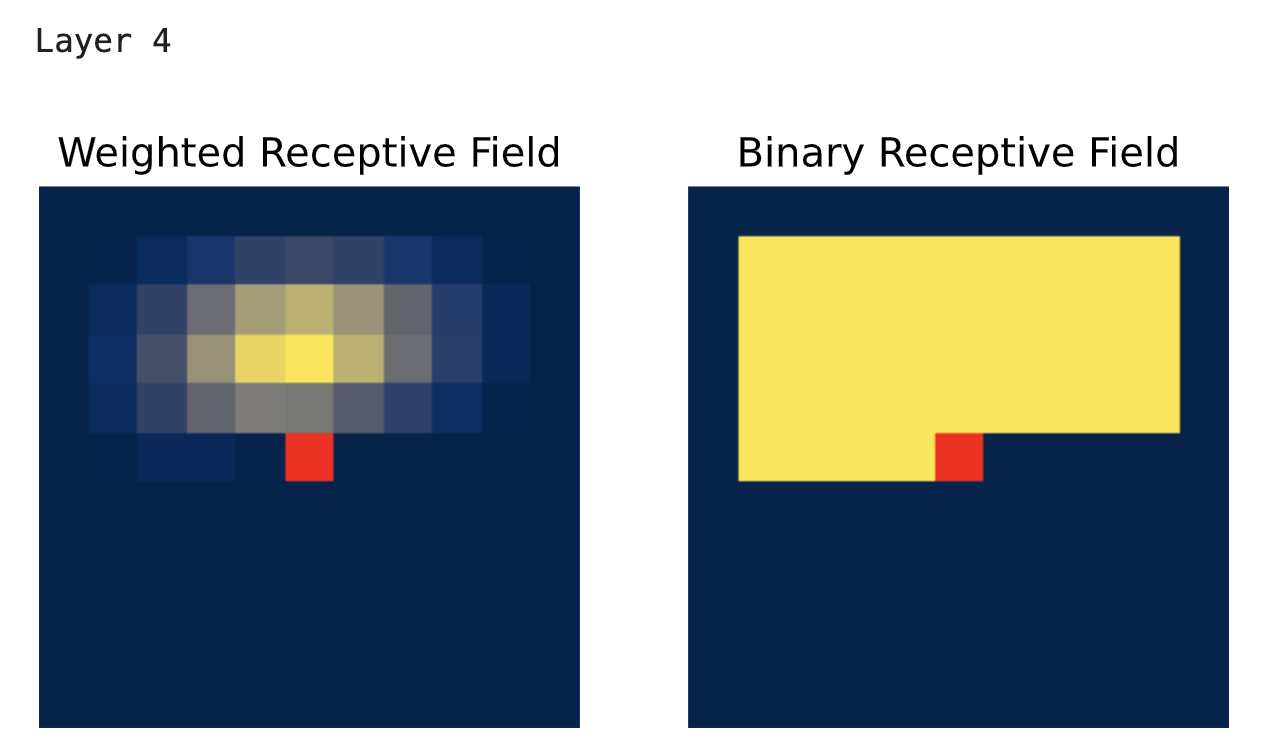

show_center_recep_field(inp_img, vert_img)

正如我们之前所讨论的,垂直卷积堆叠只关注我们想要预测的像素上方的那些像素。
最后一步,让我们清理一下仍然保留在内存中用于可视化感受野的计算图:
del inp_img, horiz_conv, vert_conv
2 门控像素卷积神经网络与采样
在接下来的步骤中,我们将使用掩码卷积来构建一个完整的自回归模型,称为门控像素卷积神经网络(Gated PixelCNN)。
2.1 门控卷积
在可视化感受野时,我们假设了一个非常简化的垂直和水平卷积堆叠结构。
显然,存在更复杂精细的实现方式,而像素卷积神经网络(PixelCNN)为此采用了门控卷积。
门控卷积模块结构示意图:
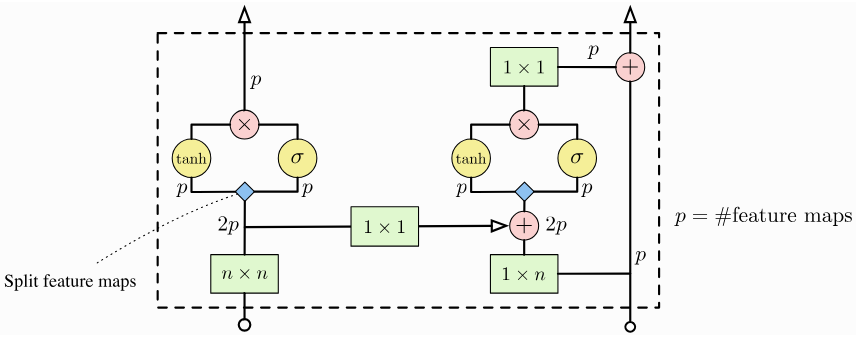
图3 门控卷积模块结构示意图
左路是垂直卷积堆叠( N × N N\times N N×N 卷积会进行相应的掩码处理),右路是水平卷积堆叠。门控卷积的实现方式是将输出通道数设置为原来的两倍,然后通过双曲正切函数( tanh \tanh tanh)和 Sigmoid 函数的逐元素相乘来组合这些通道。对于一个线性层,我们可以将门控激活单元表示如下:
y = tanh ( W f x ) ⊙ σ ( W g x ) \mathbf{y} = \tanh\left(\mathbf{W}_{f}\mathbf{x}\right)\odot\sigma\left(\mathbf{W}_{g}\mathbf{x}\right) y=tanh(Wfx)⊙σ(Wgx)
为简便起见,这里忽略了偏置项,并将线性层拆分为两部分,即 W f \mathbf{W}_{f} Wf 和 W g \mathbf{W}_{g} Wg。这一概念与长短期记忆网络(LSTM)中的输入门和调制门类似,并且也已在许多其他架构中得到应用。这种门控激活机制背后的主要动机在于,它或许能够对更复杂的交互进行建模,并且能简化学习过程。
除了门控卷积之外,我们还可以看到水平卷积堆叠使用了残差连接,而垂直卷积堆叠则没有。这是因为我们使用水平卷积堆叠的输出来进行预测。垂直卷积堆叠中的每一个卷积层也能接收到较强的梯度信号,因为它距离残差连接仅有两个 1 × 1 1\times 1 1×1 卷积层的距离,所以不需要再为其前面的所有层都添加残差连接。
下面是具体实现的代码块:
class GatedMaskedConv(nn.Module):
def __init__(self, c_in, **kwargs):
"""
门控卷积模块实现了上面展示的计算图。
"""
super().__init__()
self.conv_vert = VerticalStackConvolution(c_in, c_out=2*c_in, **kwargs)
self.conv_horiz = HorizontalStackConvolution(c_in, c_out=2*c_in, **kwargs)
self.conv_vert_to_horiz = nn.Conv2d(2*c_in, 2*c_in, kernel_size=1, padding=0)
self.conv_horiz_1x1 = nn.Conv2d(c_in, c_in, kernel_size=1, padding=0)
def forward(self, v_stack, h_stack):
# 垂直卷积堆叠(左路)
v_stack_feat = self.conv_vert(v_stack)
v_val, v_gate = v_stack_feat.chunk(2, dim=1)
v_stack_out = torch.tanh(v_val) * torch.sigmoid(v_gate)
# 水平卷积堆叠(右路)
h_stack_feat = self.conv_horiz(h_stack)
h_stack_feat = h_stack_feat + self.conv_vert_to_horiz(v_stack_feat)
h_val, h_gate = h_stack_feat.chunk(2, dim=1)
h_stack_feat = torch.tanh(h_val) * torch.sigmoid(h_gate)
h_stack_out = self.conv_horiz_1x1(h_stack_feat)
h_stack_out = h_stack_out + h_stack
return v_stack_out, h_stack_out
2.2 构建模型
利用门控卷积,我们现在可以构建像素卷积神经网络(PixelCNN)模型了。
该架构由多个堆叠的门控掩码卷积(GatedMaskedConv)模块组成,其中我们对部分卷积添加了额外的膨胀因子。
这样做是为了增大模型的感受野,从而在生成过程中能够考虑更大范围的上下文信息。
卷积中的膨胀操作的工作方式如下,膨胀操作:
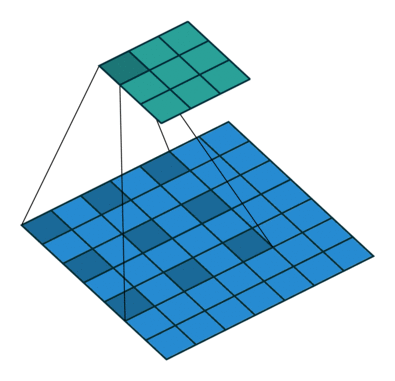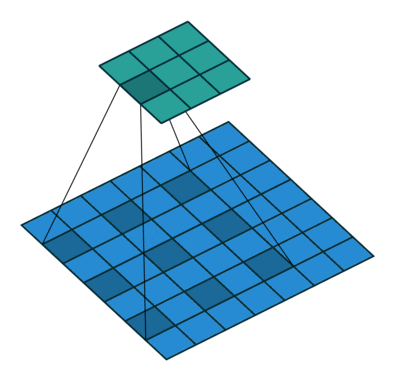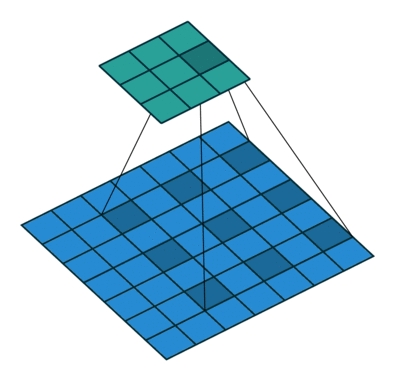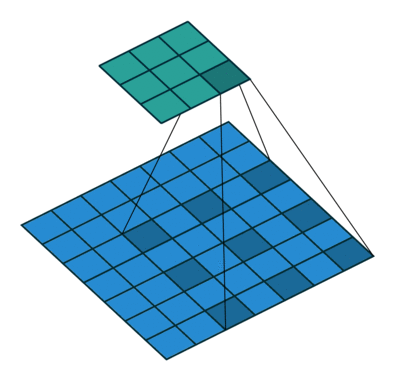
图4 膨胀操作示意图
请注意,输出尺寸变小仅仅是因为动画假设没有进行填充。在我们的实现中,会对输入图像进行相应的填充。除了使用空洞卷积,我们也可以对输入进行下采样,并采用类似 PixelCNN++ 中的编解码器架构。
下面,我们将把 PixelCNN 模型实现为一个 PyTorch Lightning 模块。除了堆叠的门控卷积层,我们还有对中心像素进行掩码处理的初始水平和垂直卷积层,以及一个将输出特征映射为类别预测结果的最终 1 × 1 1\times 1 1×1 卷积层。为了确定一批图像的似然性,我们首先使用掩码后的水平和垂直输入卷积创建初始特征。接着,将这些特征输入到堆叠的门控卷积层中进行前向传播。最后,取水平卷积堆叠的输出特征,并应用 1 × 1 1\times 1 1×1 卷积进行分类。
from tqdm import tqdm
class PixelCNN(pl.LightningModule):
def __init__(self, c_in, c_hidden):
super().__init__()
self.save_hyperparameters()
# 跳过中心像素的初始卷积操作
self.conv_vstack = VerticalStackConvolution(c_in, c_hidden, mask_center=True)
self.conv_hstack = HorizontalStackConvolution(c_in, c_hidden, mask_center=True)
# 像素卷积神经网络(PixelCNN)的卷积模块。我们使用空洞卷积(膨胀卷积)而不是下采样的方式。
self.conv_layers = nn.ModuleList([
GatedMaskedConv(c_hidden),
GatedMaskedConv(c_hidden, dilation=2),
GatedMaskedConv(c_hidden),
GatedMaskedConv(c_hidden, dilation=4),
GatedMaskedConv(c_hidden),
GatedMaskedConv(c_hidden, dilation=2),
GatedMaskedConv(c_hidden)
])
# 输出分类卷积层(1×1 卷积层)
self.conv_out = nn.Conv2d(c_hidden, c_in * 256, kernel_size=1, padding=0)
self.example_input_array = train_set[0][0][None]
def forward(self, x):
"""
将图像输入模型进行前向传播,并返回每个像素的逻辑值(logits)。
输入:
x - 图像张量,其整数值介于 0 到 255 之间。
"""
# 将输入从 0 到 255 的范围重新缩放到 -1 到 1 的范围
x = (x.float() / 255.0) * 2 - 1
# 初始卷积层
v_stack = self.conv_vstack(x)
h_stack = self.conv_hstack(x)
# 门控卷积层
for layer in self.conv_layers:
v_stack, h_stack = layer(v_stack, h_stack)
# 1x1 分类卷积层
# 在 1x1 卷积之前应用 ELU 激活函数,以便在残差连接上引入非线性变换
out = self.conv_out(F.elu(h_stack))
# 输出维度:[批次大小,类别数量,通道数,高度,宽度]
out = out.reshape(out.shape[0], 256, out.shape[1]//256, out.shape[2], out.shape[3])
return out
def calc_likelihood(self, x):
# 前向传播并计算每维度比特数(bpd)似然值
pred = self.forward(x)
nll = F.cross_entropy(pred, x, reduction='none')
bpd = nll.mean(dim=[1,2,3]) * np.log2(np.exp(1))
return bpd.mean()
@torch.no_grad()
def sample(self, img_shape, img=None):
"""
自回归模型的采样函数。
输入:
img_shape - 要生成的图像的形状(批次大小 B、通道数 C、高度 H、宽度 W)
img(可选) - 如果提供了该张量,它将被用作起始图像。输入张量中需要填充的像素值应为 -1。
"""
# 创建空图像
if img is None:
img = torch.zeros(img_shape, dtype=torch.long).to(device) - 1
else:
img = img.clone()
# 生成循环
for h in tqdm(range(img_shape[2]), position=0, leave=True, desc="Sampling", mininterval=1):
for w in range(img_shape[3]):
for c in range(img_shape[1]):
# 如果该位置不需要填充(值为 -1)则跳过
if (img[:,c,h,w] != -1).all().item():
continue
# 为了提高效率,我们只需输入图像的上半部分
# 因为无论如何,掩码卷积都会跳过其他部分
pred = self.forward(img[:,:,:h+1,:])
probs = F.softmax(pred[:,:,c,h,w], dim=-1)
img[:,c,h,w] = torch.multinomial(probs, num_samples=1).squeeze(dim=-1)
return img
def configure_optimizers(self):
optimizer = optim.Adam(self.parameters(), lr=1e-3)
scheduler = optim.lr_scheduler.StepLR(optimizer, 1, gamma=0.99)
return [optimizer], [scheduler]
def training_step(self, batch, batch_idx):
loss = self.calc_likelihood(batch[0])
self.log('train_bpd', loss)
return loss
def validation_step(self, batch, batch_idx):
loss = self.calc_likelihood(batch[0])
self.log('val_bpd', loss)
def test_step(self, batch, batch_idx):
loss = self.calc_likelihood(batch[0])
self.log('test_bpd', loss)
要从自回归模型中进行采样,我们需要遍历输入的所有维度。我们从一张空白图像开始,从左上角开始逐个填充像素。请注意,在预测像素 x i x_i xi 时,其下方的所有像素对该预测没有影响。因此,我们可以在不改变预测结果的情况下裁剪图像的高度,同时提高效率。不过,采样函数中的所有循环已经表明,采样会花费我们相当长的时间。在循环迭代过程中,有很多计算是可以复用的,因为已预测像素上的特征在迭代过程中不会改变。然而,实现这一点需要付出相当多的努力,并且在实际实现中通常不会这么做,因为归根结底,自回归采样本质上是顺序进行的,速度较慢。因此,我们在这里采用默认的实现方式。
在训练模型之前,我们可以在一张尺寸为 28 × 28 28\times 28 28×28 的 MNIST 图像上检查模型的完整感受野:
test_model = PixelCNN(c_in=1, c_hidden=64)
inp = torch.zeros(1,1,28,28)
inp.requires_grad_()
out = test_model(inp)
show_center_recep_field(inp, out.squeeze(dim=2))
del inp, out, test_model

2.3 获取并加载模型
为了训练模型,我们可以再次借助 PyTorch Lightning 来实现。并且,我们可以编写一个函数,用于在预训练模型存在时加载它。为了降低计算成本,我们直接获取预训练模型,跳过训练。
- 获取模型文件并解压
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_models/dca5faf02d4011f08d8ffa163edcddae/PixelCNN.tar.gz
!tar -zxvf PixelCNN.tar.gz
- 加载模型
def train_model(**kwargs):
# 创建一个带有生成回调函数的 PyTorch Lightning 训练器
trainer = pl.Trainer(default_root_dir=os.path.join(CHECKPOINT_PATH, "PixelCNN"),
accelerator="cpu",
devices=1,
max_epochs=150,
callbacks=[ModelCheckpoint(save_weights_only=True, mode="min", monitor="val_bpd"),
LearningRateMonitor("epoch")])
result = None
# 检查预训练模型是否存在。如果存在,则加载该模型并跳过训练过程。
pretrained_filename = os.path.join(CHECKPOINT_PATH, "PixelCNN.ckpt")
if os.path.isfile(pretrained_filename):
print("找到预训练模型,正在加载...")
model = PixelCNN.load_from_checkpoint(pretrained_filename)
ckpt = torch.load(pretrained_filename, map_location=device)
result = ckpt.get("result", None)
else:
model = PixelCNN(**kwargs)
trainer.fit(model, train_loader, val_loader)
model = model.to(device)
if result is None:
# 在验证集和测试集上测试最佳模型
val_result = trainer.test(model, val_loader, verbose=False)
test_result = trainer.test(model, test_loader, verbose=False)
result = {"test": test_result, "val": val_result}
return model, result
- 当使用一个预训练模型调用训练函数时,我们会自动加载该模型并打印出它在测试集上的性能表现。
model, result = train_model(c_in=1, c_hidden=64)
test_res = result["test"][0]
print("测试每维度比特数:%4.3fbpd" % (test_res["test_loss"] if "test_loss" in test_res else test_res["test_bpd"]))
num_params = sum([np.prod(param.shape) for param in model.parameters()])
print("参数数量:{:,}".format(num_params))
out:
参数数量:852,160
与多尺度归一化流模型相比,像素卷积神经网络(PixelCNN)的参数数量要少得多。
当然,参数的数量取决于我们对超参数的选择。
尽管如此,一般来说,基于上述原因,可以说自回归模型要达到良好的性能,所需的参数数量比归一化流模型少得多。不过,自回归模型在采样时比归一化流模型慢得多,这限制了它们的潜在应用范围。
2.4 采样
2.4.1 生成数字(图像)
定性分析生成模型的一种方法是查看实际的样本。
因此,让我们使用我们的采样函数来生成一些数字(图像)吧:
pl.seed_everything(1)
samples = model.sample(img_shape=(16,1,28,28))
show_imgs(samples.cpu())

大多数样本都能被识别为数字,总体而言,我们得到的样本质量比使用归一化流模型时更好。
不过,我们也看到仍有改进的空间,因为相当一部分样本无法被识别(例如第一行的样本)。预计更深层的自回归模型能够达到更好的质量,因为在生成像素时,它们可以考虑更多的上下文信息。
训练好的模型本身并不局限于任何特定的图像尺寸。但是,如果我们实际采样的图像尺寸比训练数据集中的图像尺寸更大,那么在测试期间改变图像尺寸会使模型产生困惑,从而生成抽象的图形。
2.4.2 自动补全
自回归模型的一个常见应用是对图像进行自动补全。由于自回归模型是逐个预测像素的,我们可以将前 N N N 个像素设置为预定义的值,然后查看模型如何补全整幅图像。为了实现这一点,我们只需要在采样循环中跳过那些已经具有不等于 -1 的值的迭代。在下面的代码单元中,我们从训练集中随机选取三张图像,对图像的下半部分进行遮罩处理,然后让模型对其进行自动补全。为了观察样本的多样性,我们对每张图像进行 12 次这样的操作:
def autocomplete_image(img):
# 移除图像的下半部分
img_init = img.clone()
img_init[:,10:,:] = -1
print("Original image and input image to sampling:")
show_imgs([img,img_init])
# 生成12个示例补全内容
img_init = img_init.unsqueeze(dim=0).expand(12,-1,-1,-1).to(device)
img_init = img_init.clone()
pl.seed_everything(1)
img_generated = model.sample(img_init.shape, img_init)
print("Autocompletion samples:")
show_imgs(img_generated)
for i in range(1,4):
img = train_set[i][0]
autocomplete_image(img)






对于前两个数字(7 和 6),我们看到这 12 个样本生成的形状都与原始数字相似。不过,在书写数字 7 的风格上存在一些差异,而且样本中有些数字 6 出现了变形。当对下面的数字 9 进行自动补全时,我们发现模型可以生成多种与之匹配的数字。我们得到了数字 0、3、8 和 9 等不同的样本。这表明,尽管自回归模型没有隐空间,但我们仍然可以从该模型中获得多样化的样本。
2.4.3 预测分布(softmax)的可视化
自回归模型通过对 256 个值应用 softmax 函数来预测下一个像素。这赋予了模型很大的灵活性,因为如果有必要,每个像素值的概率都可以独立学习。然而,这些值实际上并非相互独立,因为像素值 32 和 33 之间的差距要比 32 和 255 之间的差距小得多。接下来,我们将对模型预测的 softmax 分布进行可视化,以便深入了解模型是如何学习相邻像素之间的关系的。
为了实现这一点,我们首先在一批图像上运行模型,并存储输出的 softmax 分布:
det_loader = data.DataLoader(train_set, batch_size=128, shuffle=False, drop_last=False)
imgs,_ = next(iter(det_loader))
imgs = imgs.to(device)
with torch.no_grad():
out = model(imgs)
out = F.softmax(out, dim=1)
mean_out = out.mean(dim=[0,2,3,4]).cpu().numpy()
out = out.cpu().numpy()
在深入研究该模型之前,让我们先可视化整个数据集中像素值的分布情况:
sns.set()
plot_args = {"color": to_rgb("C0")+(0.5,), "edgecolor": "C0", "linewidth": 0.5, "width": 1.0}
plt.hist(imgs.view(-1).cpu().numpy(), bins=256, density=True, **plot_args)
plt.yscale("log")
plt.xticks([0,64,128,192,256])
plt.show()
plt.close()
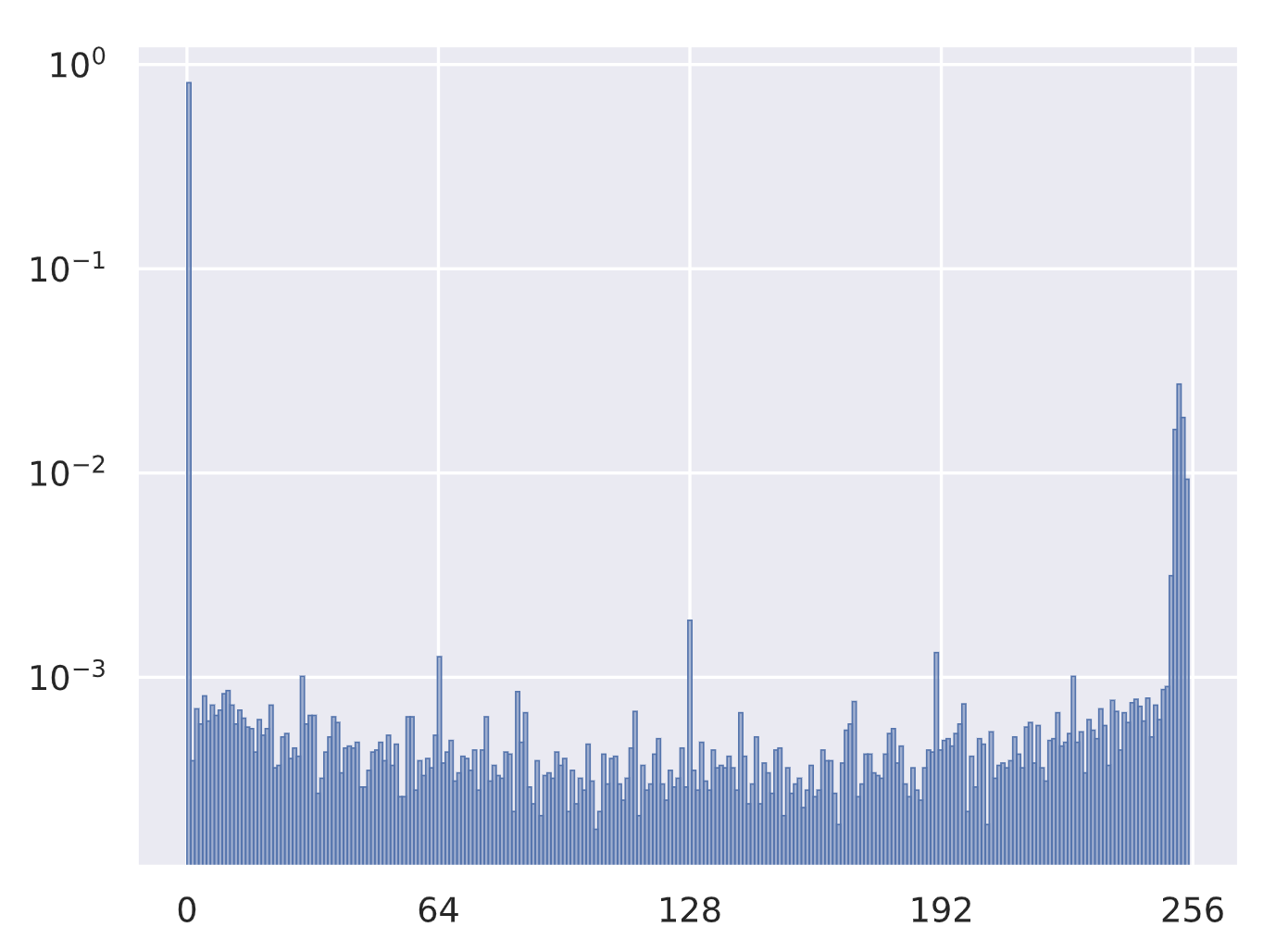
正如我们从已看过的图像中所预期的那样,像素值 0(黑色)是占主导地位的值,其次是一批介于 250 到 255 之间的值。请注意,由于数据集中存在很大的不平衡性,我们在纵轴上使用了对数刻度。有趣的是,像素值 64、128 和 191 也很突出,这很可能是由于在创建数据集过程中使用了量化操作。对于 RGB 图像,我们还会在 0 和 255 附近看到两个峰值,但中间的值出现的频率会比在 MNIST 数据集中高得多。
接下来,我们可以可视化我们的模型所预测的分布情况(取平均值):
plt.bar(np.arange(mean_out.shape[0]), mean_out, **plot_args)
plt.yscale("log")
plt.xticks([0,64,128,192,256])
plt.show()
plt.close()
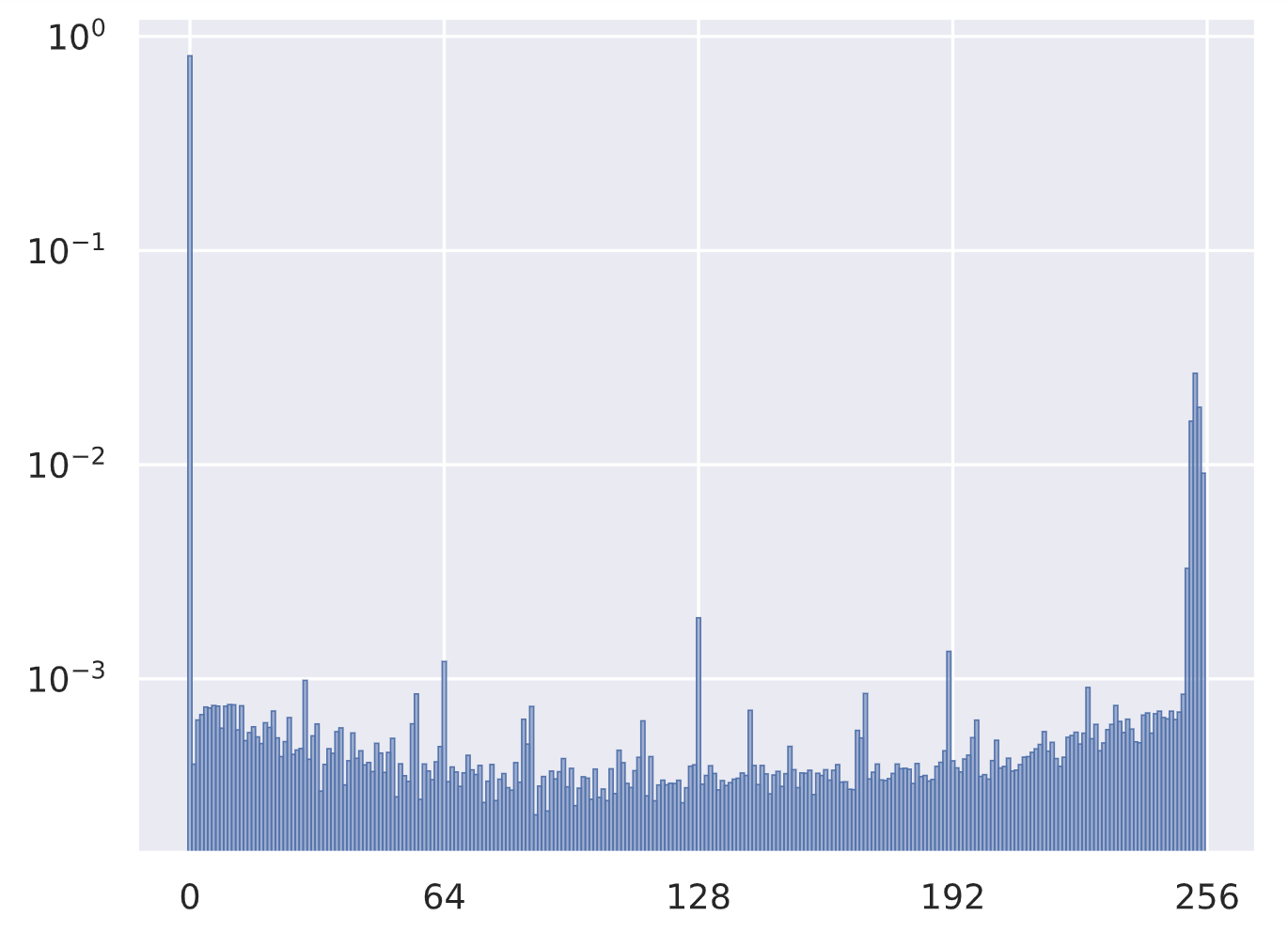
这种分布与实际数据集的分布非常接近。总体而言,这是一个好迹象,但我们可以看到,其直方图比上面(实际数据集的直方图)稍微平滑一些。
最后,为了更深入地探究所学习到的像素值之间的关系,我们可以将单个像素预测的分布情况可视化,从而获得更直观的理解。为此,我们随机选取了4张图像和若干像素点,并在下方展示它们的分布情况:
fig, ax = plt.subplots(2,2, figsize=(10,6))
for i in range(4):
ax_sub = ax[i//2][i%2]
ax_sub.bar(np.arange(out.shape[1], dtype=np.int32), out[i+4,:,0,14,14], **plot_args)
ax_sub.set_yscale("log")
ax_sub.set_xticks([0,64,128,192,256])
plt.show()
plt.close()

总体而言,我们看到了一系列非常多样化的分布,通常在数值 0 和接近 1 的地方会出现峰值。然而,第一行的分布显示出一种可能不太理想的情况。例如,尽管有的数值极为接近,但出现的概率能相差将近100倍,而且常常难以区分。这表明该模型可能没有很好地对像素值进行泛化。解决这个问题的更好办法是使用离散逻辑斯蒂混合分布,而不是 softmax 分布。可以把离散逻辑斯蒂分布想象成经过离散化、分箱处理的高斯分布。使用离散逻辑斯蒂混合分布而非 softmax 分布,会给模型引入一种归纳偏置,使得模型为相近的像素值赋予相似的出现概率。我们可以在下面对离散逻辑斯蒂分布进行可视化展示:
mu = torch.Tensor([128])
sigma = torch.Tensor([2.0])
def discrete_logistic(x, mu, sigma):
return torch.sigmoid((x+0.5-mu)/sigma) - torch.sigmoid((x-0.5-mu)/sigma)
x = torch.arange(256)
p = discrete_logistic(x, mu, sigma)
# 可视化
plt.figure(figsize=(6,3))
plt.bar(x.numpy(), p.numpy(), **plot_args)
plt.xlim(96,160)
plt.title("Discrete Logistic Distribution")
plt.xlabel("Pixel value")
plt.ylabel("Probability")
plt.show()
plt.close()
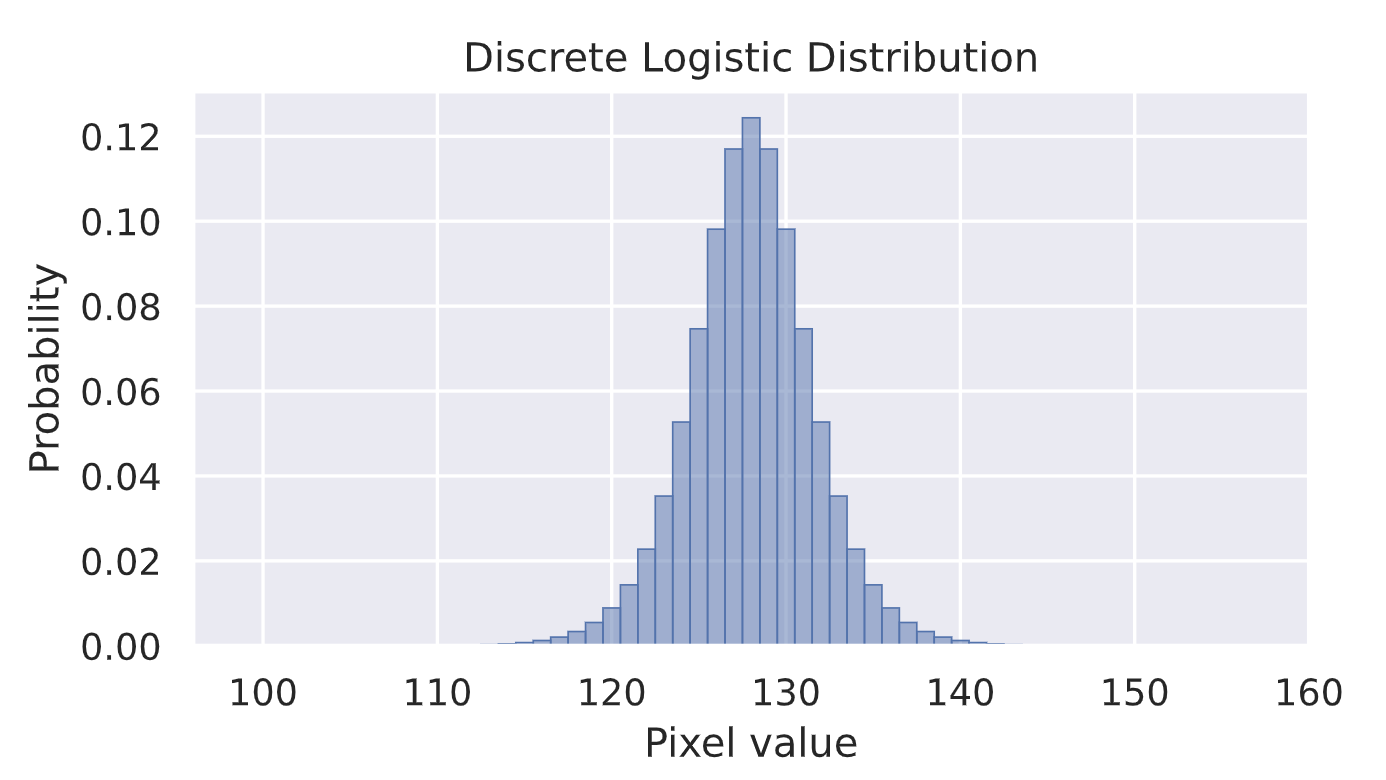
该模型不会输出 softmax 结果,而是会输出我们在混合模型中所使用的 K K K 个逻辑斯蒂分布的均值和标准差。这是像素卷积神经网络++(PixelCNN++)与最初的像素卷积神经网络(PixelCNN)相比,在自回归模型方面所引入的改进之一。
- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用






















 742
742

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








