- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用
元学习 —— 学会学习
学习目标
本课程旨在帮助学员深入理解元学习算法ProtoNet和ProtoMAML的原理与实现,掌握少样本分类任务的解决方法,学会在不同数据集上训练和测试模型,并分析模型性能,从而根据实际需求选择合适的元学习算法。
相关知识点
- 元学习算法
学习内容
1 元学习算法
1.1 元学习概述
本课程将讨论能够学习模型的算法,这些模型可以快速适应新类别以及任务,仅需少量样本。机器学习的这一领域被称为元学习,旨在实现“学会学习”。从极少数样本中学习是人类的自然能力。与当前的深度学习模型不同,我们只需看到少数警车或消防车的样本,便能在日常交通中识别它们。这种能力至关重要,因为在现实世界的应用中,数据很少保持静态,通常会随时间变化。例如,一个基于2000年的数据训练的手机目标检测系统,在检测当今常见的手机方面会有困难,因此,需要在不进行过多标注工作的情况下适应新数据。目前的优化技术在应对这一问题时存在困难,因为它们仅旨在在测试集上取得良好性能,而测试集的数据与训练数据相似。然而,如果测试集包含训练集中没有的类别呢?或者,如果我们想在完全不同的任务上测试模型呢?
元学习为这些情况提供了解决方案,这里将讨论三种流行的算法:原型网络 、与模型无关的元学习(MAML) 和 Proto-MAML 。实验将重点讨论训练集和测试集具有不同类别集合的少样本分类任务。例如,我们可以在训练阶段对猫-鸟和花-自行车的二分类问题进行建模,但在测试阶段,模型需要从每类4个示例中学习区分狗和水獭,这两个类别在训练期间未见过。
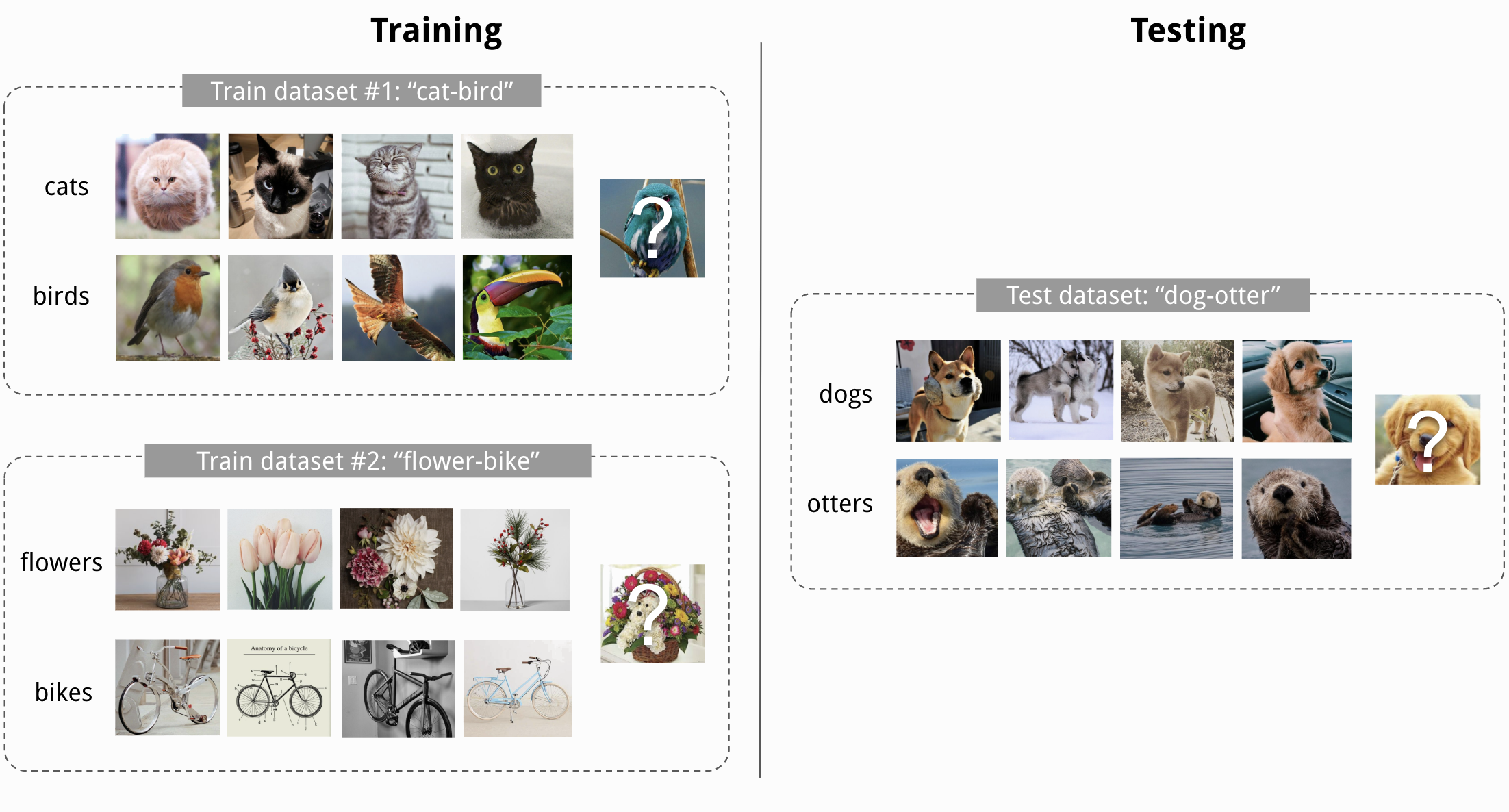
图1:元学习示意图
另一种在强化学习及近期自然语言处理领域中极为常见的重要设定,是聚焦于实现快速适应一个全新任务的少样本学习。例如,一个机器人智能体在学会奔跑、跳跃和搬运箱子后,理应具备迅速适应收集并堆叠箱子任务的能力;在自然语言处理层面,假定一个模型已在情感分类、仇恨言论检测和讽刺分类等任务上接受过训练,那么它可以进一步适应文本情感分类任务。在本课程中所探讨的所有方法,都可以轻松地应用于上述这些设定,原因在于我们仅需采用不同的 “任务” 定义即可。针对少样本分类问题,我们所考量的一个任务是区分 M 个新的类别。在此情境下,我们不仅面临新的类别,还涉及一个全新的数据集。
1.2 少样本分类
这里对实验进行一些准备,首先从导入标准库开始。实验将使用pytorch_lightning库。
%pip install seaborn==0.13.2
%pip install pytorch_lightning==2.5.2
%pip install wheel==0.44.0
## 标准库
import os
import numpy as np
import random
import json
from PIL import Image
from collections import defaultdict
from statistics import mean, stdev
from copy import deepcopy
## 绘图导入
import matplotlib.pyplot as plt
plt.set_cmap('cividis') # 设置颜色映射
# %matplotlib inline # 在 Jupyter Notebook 中直接显示图像(如果需要)
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf') # 设置导出格式
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2.0 # 设置线条宽度
import seaborn as sns
sns.reset_orig() # 重置样式
## 进度条(用于加载条)
from tqdm.auto import tqdm
## PyTorch
import torch
import torch_npu
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import torch.optim as optim
## Torchvision
import torchvision
from torchvision.datasets import CIFAR100, SVHN # 导入数据集类
from torchvision import transforms # 导入图像转换工具
# PyTorch Lightning
try:
import pytorch_lightning as pl
except ModuleNotFoundError: # 如果环境中未安装 PyTorch Lightning,则自动安装
!pip install --quiet pytorch-lightning>=1.4
import pytorch_lightning as pl
from pytorch_lightning.callbacks import LearningRateMonitor, ModelCheckpoint # 导入回调模块
# 数据集下载路径(例如 CIFAR10)
DATASET_PATH = "./data"
# 预训练模型保存路径
CHECKPOINT_PATH = "./saved_models/tutorial16"
# 设置随机种子
pl.seed_everything(42)
# 确保在所有操作都是确定性的,以保证可重复性
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
device = torch.device("npu:0") if torch_npu.npu.is_available() else torch.device("cpu") # 检测设备
print("Device:", device) # 输出设备信息
ProtoMAML 和 ProtoNet 都是小样本学习领域的模型,它们通过原型(prototype)的概念来快速适应新任务。ProtoMAML 基于 MAML(Model-Agnostic Meta-Learning), 结合了原型网络(Prototypical Networks)的思想。ProtoNet 则通过计算支持集中各类别的样本特征的均值,生成各类别的原型。在分类时,将查询集样本映射到同一特征空间后,计算其与各类别原型的相似度,根据相似度确定查询集样本的类别。
实际训练模型可能需要 2 到 8 个小时,而某些算法的评估时间则在几分钟以内。因此,实验直接使用预训练模型和训练结果。可以在下方下载ProtoMAML 和 ProtoNet的预训练模型和结果。
# 模型和结果
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_models/ca9f1dc845c811f0ad5afa163edcddae/saved_models.zip
!unzip saved_models.zip
在本课程中将使用 CIFAR100 数据集,它有 100 个类别,每个类别有 600 张大小为 32×32 像素的图像。我们不是按照示例划分训练集、验证集和测试集,而是按照类别划分: 80 个类别进行训练,10 个进行验证,10 个进行测试。我们的总体目标是获得一个能够在仅看到很少示例的情况下区分 10 个测试类别的模型。
# 数据集
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/ca9f8ca445c811f0ad5afa163edcddae/data.zip
!unzip data.zip
1.2.1 数据预处理
这里先加载数据集并可视化一些示例。
# 加载 CIFAR100 数据集
CIFAR_train_set = CIFAR100(root=DATASET_PATH, train=True, download=False, transform=transforms.ToTensor())
CIFAR_test_set = CIFAR100(root=DATASET_PATH, train=False, download=False, transform=transforms.ToTensor())
# 可视化一些样例
NUM_IMAGES = 12
CIFAR_images = torch.stack([CIFAR_train_set[np.random.randint(len(CIFAR_train_set))][0] for idx in range(NUM_IMAGES)], dim=0)
img_grid = torchvision.utils.make_grid(CIFAR_images, nrow=6, normalize=True, pad_value=0.9)
img_grid = img_grid.permute(1, 2, 0)
plt.figure(figsize=(8,8))
plt.title("Image examples of the CIFAR100 dataset")
plt.imshow(img_grid)
plt.axis('off')
plt.show()
plt.close()

接下来,我们需要按照之前提到的训练、验证和测试划分来准备数据集。torchvision 包将训练集和测试集作为两个单独的数据集对象提供。接下来的代码单元将合并原始的训练集和测试集,然后创建新的训练 - 验证 - 测试划分。
# 合并原始训练集和测试集
CIFAR_all_images = np.concatenate([CIFAR_train_set.data, CIFAR_test_set.data], axis=0) # 沿第 0 轴(样本轴)拼接图像数据
CIFAR_all_targets = torch.LongTensor(CIFAR_train_set.targets + CIFAR_test_set.targets) # 将训练集和测试集的标签合并,并转换为 PyTorch 长整型张量
为了更方便地处理数据集,下方定义了一个简单的数据集类。它接收一组图像、标签以及图像变换,并逐元素返回相应的图像和标签。
class ImageDataset(data.Dataset):
def __init__(self, imgs, targets, img_transform=None):
"""
Inputs:
imgs - Numpy array of shape [N,32,32,3] containing all images.
targets - PyTorch array of shape [N] containing all labels.
img_transform - A torchvision transformation that should be applied
to the images before returning. If none, no transformation
is applied.
"""
super().__init__()
self.img_transform = img_transform
self.imgs = imgs
self.targets = targets
def __getitem__(self, idx):
img, target = self.imgs[idx], self.targets[idx]
img = Image.fromarray(img)
if self.img_transform is not None:
img = self.img_transform(img)
return img, target
def __len__(self):
return self.imgs.shape[0]
现在可以创建类别划分。我们将类别随机分配到训练集、验证集和测试集,并采用 80%-10%-10% 的比例进行划分。
torch.manual_seed(0) # 设置随机种子以保证可重复性
classes = torch.randperm(100) # 返回 0 到 99 的随机排列
train_classes, val_classes, test_classes = classes[:80], classes[80:90], classes[90:] # 将类别划分为训练集、验证集和测试集
为了直观地了解验证集和测试集的类别,我们在下方打印类别名称:
# 打印验证集和测试集的类别
idx_to_class = {val: key for key, val in CIFAR_train_set.class_to_idx.items()}
print("Validation classes:", [idx_to_class[c.item()] for c in val_classes])
print("Test classes:", [idx_to_class[c.item()] for c in test_classes])
out:
Validation classes: ['caterpillar', 'castle', 'skunk', 'ray', 'bus', 'motorcycle', 'keyboard', 'chimpanzee', 'possum', 'tiger']
Test classes: ['kangaroo', 'crocodile', 'butterfly', 'shark', 'forest', 'pickup_truck', 'telephone', 'lion', 'worm', 'mushroom']
正如我们所看到的,这些类别具有相当的多样性,有些类别可能比其他类别更容易区分。例如,在测试类别中,“pickup_truck”是唯一的车辆类别,而类别“mushroom”、“worm”和“forest”可能更难区分。请记住,我们希望从训练集的其他 80 个类别以及实际测试类别的少量样本中学习这十个类别的分类。我们将对每个类别的样本数量进行实验。
最后,我们可以根据上述划分创建训练集、验证集和测试集。为此,我们创建了之前定义的 ImageDataset 类的数据集对象。
def dataset_from_labels(imgs, targets, class_set, **kwargs):
class_mask = (targets[:,None] == class_set[None,:]).any(dim=-1)
return ImageDataset(imgs=imgs[class_mask],
targets=targets[class_mask],
**kwargs)
接下来,对数据集进行归一化处理。此外,在训练期间使用了小幅度的增强操作来防止过拟合。
# 从新训练集中预计算的统计信息
DATA_MEANS = torch.Tensor([0.5183975 , 0.49192241, 0.44651328])
DATA_STD = torch.Tensor([0.26770132, 0.25828985, 0.27961241])
test_transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(
DATA_MEANS, DATA_STD)
])
# 对于训练添加一些增强。
train_transform = transforms.Compose([transforms.RandomHorizontalFlip(),
transforms.RandomResizedCrop(
(32, 32), scale=(0.8, 1.0), ratio=(0.9, 1.1)),
transforms.ToTensor(),
transforms.Normalize(
DATA_MEANS, DATA_STD)
])
train_set = dataset_from_labels(
CIFAR_all_images, CIFAR_all_targets, train_classes, img_transform=train_transform)
val_set = dataset_from_labels(
CIFAR_all_images, CIFAR_all_targets, val_classes, img_transform=test_transform)
test_set = dataset_from_labels(
CIFAR_all_images, CIFAR_all_targets, test_classes, img_transform=test_transform)
1.2.2 数据采样
在元学习中,如何利用可用的训练数据来学习少样本适应的策略至关重要。我们讨论的三种算法都基于一个相似的理念:在训练期间模拟少样本学习。具体来说,在每个训练步骤中,我们随机选择少量类别,并为每个类别采样少量样本。这构成了我们的少样本训练批次,我们也将其称为支持集。此外,我们从相同的类别中采样第二个样本集,并将这个批次称为查询集。我们的训练目标是通过查看支持集及其对应的标签来正确分类查询集。这三种方法(ProtoNet、MAML 和 Proto-MAML)的主要区别在于它们如何利用支持集来适应训练类别。
在 PyTorch 中,我们可以通过所谓的 Sampler 来指定数据采样过程。采样器是可迭代的对象,它会返回数据元素采样顺序的索引。通常我们会在 data.DataLoader 对象中使用 shuffle=True 选项,这会创建一个返回随机顺序数据索引的采样器。在这里,我们关注的是返回对应于支持集和查询集批次的索引批次的采样器。在下方,我们实现了这样一个采样器。
class FewShotBatchSampler(object):
def __init__(self, dataset_targets, N_way, K_shot, include_query=False, shuffle=True, shuffle_once=False):
"""
输入:
dataset_targets - PyTorch 张量,表示数据元素的标签。
N_way - 每个批次中要采样的类别数。
K_shot - 每个类别中要采样的示例数。
include_query - 如果为 True,则返回大小为 N_way*K_shot*2 的批次,可以拆分为支持集和查询集。
简化了支持集和查询集采样相同类别但不同示例的实现。
shuffle - 如果为 True,则在每次迭代中重新打乱示例和类别(用于训练)。
shuffle_once - 如果为 True,则在开始时打乱一次示例和类别,但在迭代中保持不变(用于验证)。
"""
super().__init__()
self.dataset_targets = dataset_targets
self.N_way = N_way
self.K_shot = K_shot
self.shuffle = shuffle
self.include_query = include_query
if self.include_query:
self.K_shot *= 2
self.batch_size = self.N_way * self.K_shot # 每个批次的总图像数
# 按类别组织示例
self.classes = torch.unique(self.dataset_targets).tolist()
self.num_classes = len(self.classes)
self.indices_per_class = {}
self.batches_per_class = {} # 每个类别可以提供的 K-shot 批次数
for c in self.classes:
self.indices_per_class[c] = torch.where(self.dataset_targets == c)[0]
self.batches_per_class[c] = self.indices_per_class[c].shape[0] // self.K_shot
# 创建一个类别列表,我们从中选择每个批次的 N 个类别
self.iterations = sum(self.batches_per_class.values()) // self.N_way
self.class_list = [c for c in self.classes for _ in range(self.batches_per_class[c])]
if shuffle_once or self.shuffle:
self.shuffle_data()
else:
# 对于测试,我们迭代类别而不是打乱它们
sort_idxs = [i + p * self.num_classes for i, c in enumerate(self.classes) for p in range(self.batches_per_class[c])]
self.class_list = np.array(self.class_list)[np.argsort(sort_idxs)].tolist()
def shuffle_data(self):
# 打乱每个类别的示例
for c in self.classes:
perm = torch.randperm(self.indices_per_class[c].shape[0])
self.indices_per_class[c] = self.indices_per_class[c][perm]
# 打乱我们从中采样的类别列表。注意这种打乱方式不会阻止在批次中选择相同的类别两次。
# 然而,对于训练和验证,这不是问题。
random.shuffle(self.class_list)
def __iter__(self):
# 打乱数据
if self.shuffle:
self.shuffle_data()
# 采样少样本批次
start_index = defaultdict(int)
for it in range(self.iterations):
class_batch = self.class_list[it * self.N_way:(it + 1) * self.N_way] # 选择批次中的 N 个类别
index_batch = []
for c in class_batch: # 对于每个类别,选择接下来的 K 个示例并添加到批次中
index_batch.extend(self.indices_per_class[c][start_index[c]:start_index[c] + self.K_shot])
start_index[c] += self.K_shot
if self.include_query: # 如果我们返回支持集+查询集,则对它们进行排序以便于拆分
index_batch = index_batch[::2] + index_batch[1::2]
yield index_batch
def __len__(self):
return self.iterations
需要注意的是,由于采用了更简单的洗牌函数(shuffle_data),此采样器最终允许在批次中重复使用同一类别。换句话说,在训练或验证期间,如果我们为 5 类 4 样本的训练设置采样批次,那么有时可能会出现一个批次中 5 个类别中有 2 个是相同的情况。不过,由于我们有 80 个类别可供选择,这种情况相对较少发生。此外,如果元学习方法的代码支持每类别样本数和类别数的变动,那么即使出现上述情况也不会构成任何问题。然而,当类别数或任务数较少时,建议将 shuffle_data 方法替换为能够防止在同一个批次中重复选择相同类别的采样器。
现在,我们可以通过将 FewShotBatchSampler 对象作为 batch_sampler=... 参数传递给 PyTorch 数据加载器对象,来创建我们所需要的数据加载器。在我们的实验中,我们将使用 5 类 4 样本的训练设置。这意味着每个支持集包含 5 个类别,每个类别有 4 个样本,总计 20 张图片。通常,最好将样本数设置为所测试的样本数。不过,我们将在稍后尝试不同数量的样本,因此我们暂时选择 4 作为折中方案。为了获得最佳性能的模型,建议将训练样本数作为超参数进行网格搜索。
N_WAY = 5
K_SHOT = 4
train_data_loader = data.DataLoader(train_set,
batch_sampler=FewShotBatchSampler(train_set.targets,
include_query=True,
N_way=N_WAY,
K_shot=K_SHOT,
shuffle=True),
num_workers=4)
val_data_loader = data.DataLoader(val_set,
batch_sampler=FewShotBatchSampler(val_set.targets,
include_query=True,
N_way=N_WAY,
K_shot=K_SHOT,
shuffle=False,
shuffle_once=True),
num_workers=4)
为了简化操作,这里实现了支持集和查询集的采样,即采样一个支持集,其样本数量是所需数量的两倍。在从数据加载器采样一个批次后,我们需要将其拆分为支持集和查询集。可以将这一步骤总结在以下函数中:
def split_batch(imgs, targets):
support_imgs, query_imgs = imgs.chunk(2, dim=0)
support_targets, query_targets = targets.chunk(2, dim=0)
return support_imgs, query_imgs, support_targets, query_targets
最后,为了确保我们的数据采样过程实现正确,我们可以采样一个批次并可视化其支持集和查询集。我们希望看到的是支持集和查询集具有相同的类别,但样本不同。
imgs, targets = next(iter(val_data_loader)) # 我们使用验证集,因为它不应用增强
support_imgs, query_imgs, _, _ = split_batch(imgs, targets)
support_grid = torchvision.utils.make_grid(support_imgs, nrow=K_SHOT, normalize=True, pad_value=0.9)
support_grid = support_grid.permute(1, 2, 0)
query_grid = torchvision.utils.make_grid(query_imgs, nrow=K_SHOT, normalize=True, pad_value=0.9)
query_grid = query_grid.permute(1, 2, 0)
fig, ax = plt.subplots(1, 2, figsize=(8, 5))
ax[0].imshow(support_grid)
ax[0].set_title("Support set")
ax[0].axis('off')
ax[1].imshow(query_grid)
ax[1].set_title("Query set")
ax[1].axis('off')
plt.suptitle("Few Shot Batch", weight='bold')
plt.show()
plt.close()
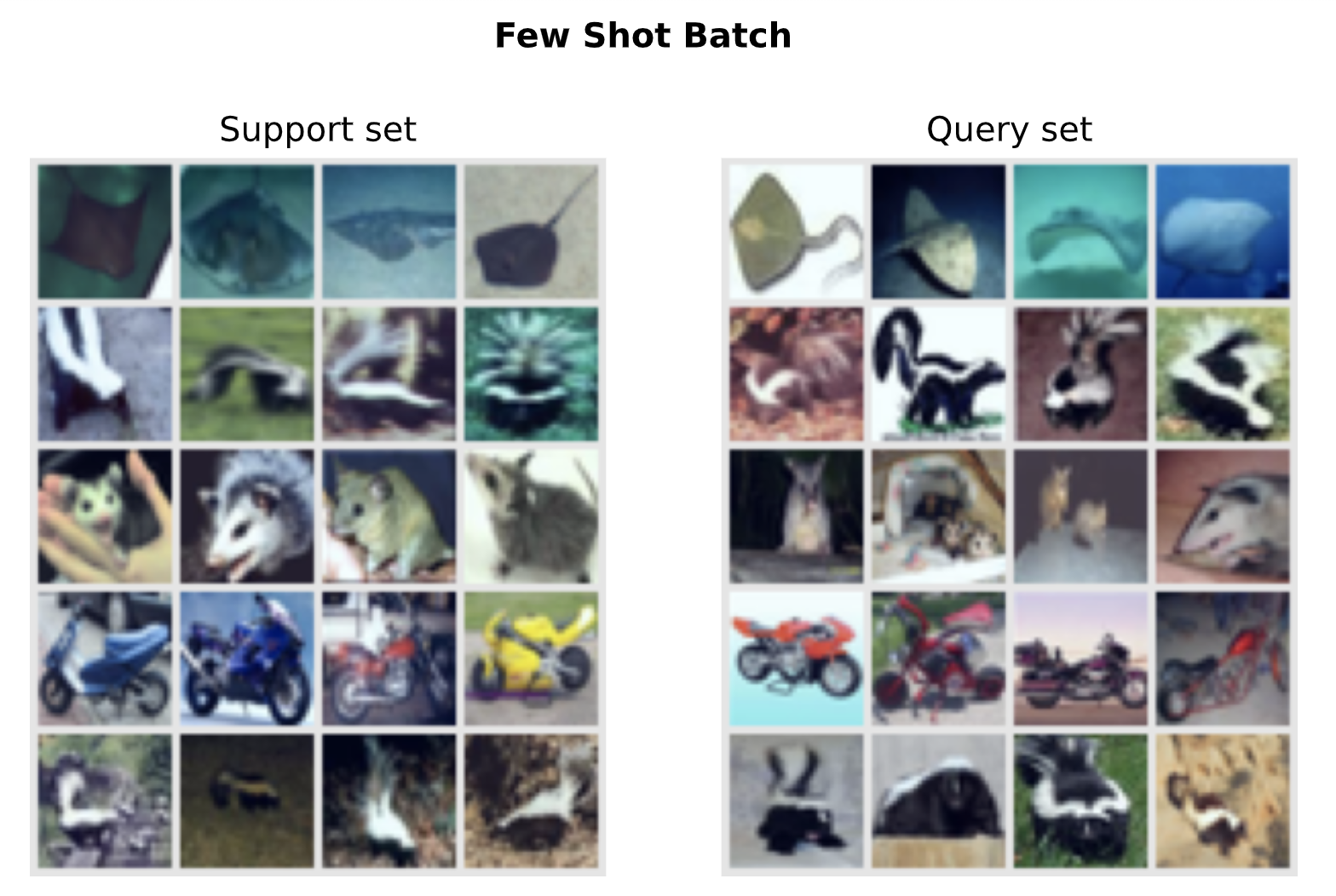
如我们所见,支持集和查询集具有相同的五个类别,但样本不同。模型的任务是通过从支持集及其标签中学习,来对查询集中的样本进行分类。在数据采样就绪后,我们现在可以开始实现我们的第一个元学习模型:原型网络。
1.3 原型网络
原型网络(ProtoNet)是一种基于度量的元学习算法,其运作方式类似于最近邻分类。基于度量的元学习方法通过某种距离函数 d φ d_{\varphi} dφ 来对新样本 x \mathbf{x} x 进行分类,该距离函数衡量 x \mathbf{x} x 与支持集中所有元素之间的距离。ProtoNets 通过在学习到的特征空间中使用原型的概念来实现这一想法。首先,ProtoNet 使用嵌入函数 f θ f_{\theta} fθ 将支持集中的每个输入编码为一个 L L L 维特征向量。接下来,对于每个类别 c c c,我们收集所有标签为 c c c 的样本的特征向量,并计算它们的平均值。形式上,我们可以将其定义为:
v c = 1 ∣ S c ∣ ∑ ( x i , y i ) ∈ S c f θ ( x i ) \mathbf{v}_c=\frac{1}{|S_c|}\sum_{(\mathbf{x}_i,y_i)\in S_c}f_{\theta}(\mathbf{x}_i) vc=∣Sc∣1(xi,yi)∈Sc∑fθ(xi)
其中 S c S_c Sc 是支持集 S S S 中 y i = c y_i=c yi=c 的部分, v c \mathbf{v}_c vc 表示类别 c c c 的原型。图2展示了在二维特征空间和三个类别情况下原型计算的可视化效果。彩色点表示编码后的支持元素及其对应的类别标签,而类别标签旁边的黑点则是平均后的原型。
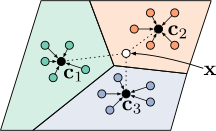
图2:原型网络类别原型示意图
基于这些原型,我们希望对新样本进行分类。由于我们想要学习编码函数 f θ f_{\theta} fθ,因此这种分类必须是可微分的,因此我们需要定义一个跨类别的概率分布。为此,我们将使用距离函数 d φ d_{\varphi} dφ:新样本 x \mathbf{x} x 越接近原型 v c \mathbf{v}_c vc, x \mathbf{x} x 属于类别 c c c 的概率就越高。形式上,我们可以在 x \mathbf{x} x 到所有类别原型的距离上简单地使用 softmax 函数:
p ( y = c ∣ x ) = softmax ( − d φ ( f θ ( x ) , v c ) ) = exp ( − d φ ( f θ ( x ) , v c ) ) ∑ c ′ ∈ C exp ( − d φ ( f θ ( x ) , v c ′ ) ) p(y=c\vert\mathbf{x})=\text{softmax}(-d_{\varphi}(f_{\theta}(\mathbf{x}), \mathbf{v}_c))=\frac{\exp\left(-d_{\varphi}(f_{\theta}(\mathbf{x}), \mathbf{v}_c)\right)}{\sum_{c'\in \mathcal{C}}\exp\left(-d_{\varphi}(f_{\theta}(\mathbf{x}), \mathbf{v}_{c'})\right)} p(y=c∣x)=softmax(−dφ(fθ(x),vc))=∑c′∈Cexp(−dφ(fθ(x),vc′))exp(−dφ(fθ(x),vc))
请注意,负号是必要的,因为我们希望增加接近向量的概率,而降低远处向量的概率。我们根据训练查询集样本的交叉熵误差来训练网络 f θ f_{\theta} fθ。因此,梯度会通过原型 v c \mathbf{v}_c vc 和查询集编码 f θ ( x ) f_{\theta}(\mathbf{x}) fθ(x) 进行传播。对于距离函数 d φ d_{\varphi} dφ,我们可以选择任何只要关于其两个输入可微的函数。这里我们使用最常见平方欧几里得距离,但也有几项工作研究了不同的距离函数。
1.3.1 ProtoNet 的实现
现在我们已经了解了 ProtoNet 的工作原理,接下来我们看看如何将其应用于少样本图像分类问题,并在下方实现它。首先,我们需要定义编码函数 $ f_{\theta} $。在这里,我们选择 DenseNet,并且不需要自行实现 DenseNet,而是可以依赖 torchvision 的模型包。我们使用常见的超参数:64 个初始特征通道,每个块增加 32 个,瓶颈大小为 64(即增长速率的两倍)。我们使用 4 个阶段,每个阶段 6 层,总共大约 100 万个参数。需要注意的是,torchvision 包假设最后一层用于分类,因此将其输出大小称为 num_classes。然而,我们可以将其用作 ProtoNet 的特征空间,并选择任意的维度。为了确保公平比较,我们将在本课程中的其他算法中使用相同的网络。
def get_convnet(output_size):
convnet = torchvision.models.DenseNet(growth_rate=32,
block_config=(6, 6, 6, 6),
bn_size=2,
num_init_features=64,
num_classes=output_size # 输出维度
)
return convnet
接下来,我们可以看看如何实现 ProtoNet。我们将把它定义为 PyTorch Lightning 模块,以便使用 PyTorch Lightning 的所有功能。训练的第一步是用我们的网络编码批次中的所有图像。接下来,我们从支持集中计算类别原型(函数 calculate_prototypes),并根据原型对查询集样本进行分类(函数 classify_feats)。请注意,我们使用之前描述的数据采样方法,将支持集和查询集一起堆叠在批次中。因此,我们使用之前定义的函数 split_batch 将它们分开。完整代码如下。
class ProtoNet(pl.LightningModule):
def __init__(self, proto_dim, lr):
"""
输入
proto_dim - 原型特征空间的维度
lr - Adam 优化器的学习率
"""
super().__init__()
self.save_hyperparameters()
self.model = get_convnet(output_size=self.hparams.proto_dim)
def configure_optimizers(self):
optimizer = optim.AdamW(self.parameters(), lr=self.hparams.lr)
scheduler = optim.lr_scheduler.MultiStepLR(
optimizer, milestones=[140, 180], gamma=0.1)
return [optimizer], [scheduler]
@staticmethod
def calculate_prototypes(features, targets):
# 给定一堆特征向量和标签,返回类别原型
# features - 形状 [N, proto_dim],targets - 形状 [N]
classes, _ = torch.unique(targets).sort() # 确定我们有哪些类别
prototypes = []
for c in classes:
p = features[torch.where(targets == c)[0]].mean(dim=0) # 平均类别特征向量
prototypes.append(p)
prototypes = torch.stack(prototypes, dim=0)
# 返回 'classes' 张量以知道哪个原型属于哪个类别
return prototypes, classes
def classify_feats(self, prototypes, classes, feats, targets):
# 使用原型对新示例进行分类并返回分类误差
dist = torch.pow(prototypes[None, :] - feats[:, None], 2).sum(dim=2) # 平方欧几里得距离
preds = F.log_softmax(-dist, dim=1)
labels = (classes[None, :] == targets[:, None]).long().argmax(dim=-1)
acc = (preds.argmax(dim=1) == labels).float().mean()
return preds, labels, acc
def calculate_loss(self, batch, mode):
# 确定给定支持集和查询集的训练损失
imgs, targets = batch
features = self.model(imgs) # 编码支持集和查询集的所有图像
support_feats, query_feats, support_targets, query_targets = split_batch(features, targets)
prototypes, classes = ProtoNet.calculate_prototypes(support_feats, support_targets)
preds, labels, acc = self.classify_feats(prototypes, classes, query_feats, query_targets)
loss = F.cross_entropy(preds, labels)
self.log(f"{mode}_loss", loss)
self.log(f"{mode}_acc", acc)
return loss
def training_step(self, batch, batch_idx):
return self.calculate_loss(batch, mode="train")
def validation_step(self, batch, batch_idx):
_ = self.calculate_loss(batch, mode="val")
对于验证,我们使用与训练相同的原理,从保留的 10 个类别中采样支持集和查询集。然而,这会根据所选的查询集和对应的支持集给我们带来噪声分数。这就是为什么我们在测试期间将使用不同的策略。对于验证,我们的训练策略已经足够,因为它比测试快得多,并且只要我们在验证迭代中保持支持集 - 查询集不变,就能很好地估计训练的泛化能力。
1.3.2 ProtoNet模型训练
实现模型后,我们就可以开始训练它了。我们使用常见的 PyTorch Lightning 训练函数,并将模型训练 200 个周期。训练函数将 model_class 作为输入参数,也就是应该被训练的 PyTorch Lightning 模块类,因为我们还将为其他算法重用此函数。
def train_model(model_class, train_loader, val_loader, **kwargs):
trainer = pl.Trainer(default_root_dir=os.path.join(CHECKPOINT_PATH, model_class.__name__),
accelerator="npu" if str(device).startswith("auto") else "cpu",
devices=1,
max_epochs=200,
callbacks=[ModelCheckpoint(save_weights_only=True, mode="max", monitor="val_acc"),
LearningRateMonitor("epoch")],
enable_progress_bar=False)
trainer.logger._default_hp_metric = None
# 检查预训练模型是否存在。如果存在,则加载它并跳过训练
pretrained_filename = os.path.join(
CHECKPOINT_PATH, model_class.__name__ + ".ckpt")
if os.path.isfile(pretrained_filename):
print(f"Found pretrained model at {pretrained_filename}, loading...")
# 自动加载保存的超参数的模型
model = model_class.load_from_checkpoint(pretrained_filename)
else:
pl.seed_everything(42) # 为了可重复性
model = model_class(**kwargs)
trainer.fit(model, train_loader, val_loader)
model = model_class.load_from_checkpoint(
trainer.checkpoint_callback.best_model_path) # 加载训练后最佳检查点
return model
下面是我们的 ProtoNet 的训练调用。我们使用 64 维特征空间。更大的特征空间显示出更嘈杂的结果,因为平方欧几里得距离的期望值成比例地更大,而更小的特征空间可能无法提供足够的灵活性。
protonet_model = train_model(ProtoNet,
proto_dim=64,
lr=2e-4,
train_loader=train_data_loader,
val_loader=val_data_loader)
我们还可以在下方仔细查看 TensorBoard。
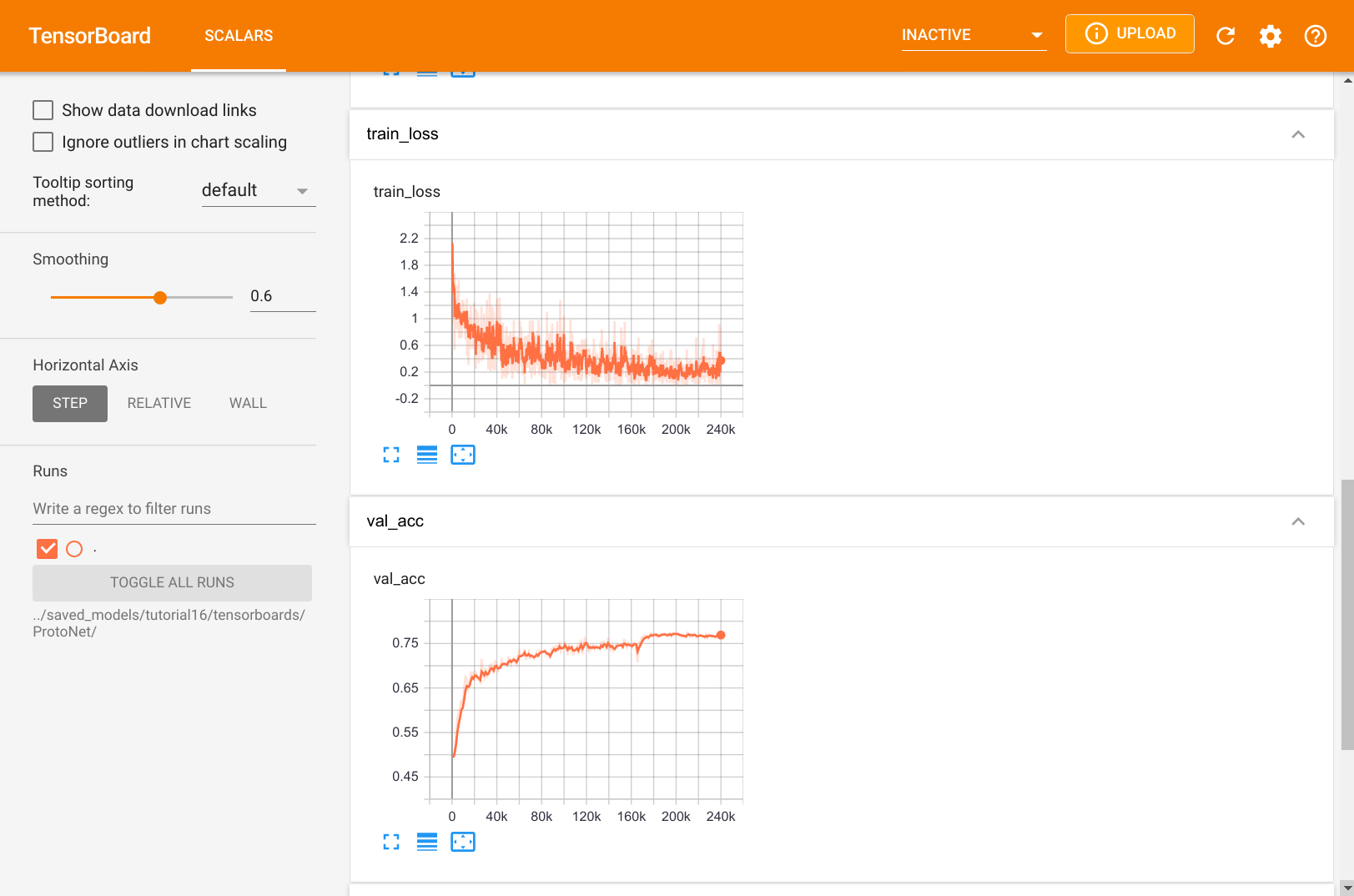
图3:ProtoNet 训练日志
与标准监督学习相比,我们看到 ProtoNet 并没有像我们预期的那样过拟合。验证准确率当然低于平均训练准确率,但训练损失并没有接近零。这是因为没有一个训练批次与其他批次相同,我们还在支持集和查询集中混合了新的示例。这使得我们在每次迭代中都有略微不同的原型,使网络更难完全过拟合。
1.3.3 ProtoNet模型测试
我们元学习的目标是获得一个能够快速适应新任务的模型,或者在这种情况下,能够区分新类别的模型。为了测试这一点,我们将使用训练好的 ProtoNet 并使其适应 10 个测试类别。为此,我们从每个类别中选取 k k k 个示例来确定原型,并在所有其他示例上测试分类准确率。这可以看作是使用每个类别的 k k k 个示例作为支持集,而数据集的其余部分作为查询集。我们遍历数据集,使得每个示例都曾被包含在一个支持集中。所有支持集上的平均性能告诉我们,当 ProtoNet 仅看到每个类别的 k k k 个示例时,其表现如何。在训练期间,我们使用 k = 4 k = 4 k=4。在测试中,我们将尝试 k = { 2 , 4 , 8 , 16 , 32 } k = \{2, 4, 8, 16, 32\} k={2,4,8,16,32} 以更好地了解 k k k 对结果的影响。我们预期支持集中的示例越多,准确率越高,但我们不知道其扩展情况。因此,我们首先实现一个函数,用于执行给定 k k k 的测试过程:
@torch.no_grad()
def test_proto_net(model, dataset, data_feats=None, k_shot=4):
"""
输入
model - 预训练的 ProtoNet 模型
dataset - 应执行测试的数据集。应为 ImageDataset 的实例
data_feats - 数据集中所有图像的编码特征。
如果为 None,则会重新计算,并返回以便后续使用。
k_shot - 支持集中每个类别的示例数。
"""
model = model.to(device)
model.eval()
num_classes = dataset.targets.unique().shape[0]
exmps_per_class = dataset.targets.shape[0] // num_classes # 这里假设示例分布均匀
# 编码器网络在不同的 k-shot 设置中保持不变。因此,我们只需提取所有图像的特征一次。
if data_feats is None:
# 数据集准备
dataloader = data.DataLoader(dataset, batch_size=128, num_workers=4, shuffle=False, drop_last=False)
img_features = []
img_targets = []
for imgs, targets in tqdm(dataloader, "Extracting image features", leave=False):
imgs = imgs.to(device)
feats = model.model(imgs)
img_features.append(feats.detach().cpu())
img_targets.append(targets)
img_features = torch.cat(img_features, dim=0)
img_targets = torch.cat(img_targets, dim=0)
# 按类别排序,以便我们获得形状为 [num_classes, exmps_per_class, ...] 的张量
# 便于后续处理
img_targets, sort_idx = img_targets.sort()
img_targets = img_targets.reshape(num_classes, exmps_per_class).transpose(0, 1)
img_features = img_features[sort_idx].reshape(num_classes, exmps_per_class, -1).transpose(0, 1)
else:
img_features, img_targets = data_feats
# 我们以两种方式遍历整个数据集。首先,选择 k-shot 批次。
# 其次,在所有其他示例上评估模型
accuracies = []
for k_idx in tqdm(range(0, img_features.shape[0], k_shot), "Evaluating prototype classification", leave=False):
# 选择支持集并计算原型
k_img_feats, k_targets = img_features[k_idx:k_idx + k_shot].flatten(0, 1), img_targets[k_idx:k_idx + k_shot].flatten(0, 1)
prototypes, proto_classes = model.calculate_prototypes(k_img_feats, k_targets)
# 在数据集的其余部分评估准确性
batch_acc = 0
for e_idx in range(0, img_features.shape[0], k_shot):
if k_idx == e_idx: # 不要在支持集示例上评估
continue
e_img_feats, e_targets = img_features[e_idx:e_idx + k_shot].flatten(0, 1), img_targets[e_idx:e_idx + k_shot].flatten(0, 1)
_, _, acc = model.classify_feats(prototypes, proto_classes, e_img_feats, e_targets)
batch_acc += acc.item()
batch_acc /= img_features.shape[0] // k_shot - 1
accuracies.append(batch_acc)
return (mean(accuracies), stdev(accuracies)), (img_features, img_targets)
如果所有图像都已处理过一次,测试 ProtoNet 会相对较快。因此,我们可以执行以下操作:
protonet_accuracies = dict()
data_feats = None
for k in [2, 4, 8, 16, 32]:
protonet_accuracies[k], data_feats = test_proto_net(protonet_model, test_set, data_feats=data_feats, k_shot=k)
print(f"Accuracy for k={k}: {100.0*protonet_accuracies[k][0]:4.2f}% (+-{100*protonet_accuracies[k][1]:4.2f}%)")
out:
Accuracy for k=2: 44.43% (±3.64%)
Accuracy for k=4: 52.19% (±2.25%)
Accuracy for k=8: 57.69% (±1.28%)
Accuracy for k=16: 62.66% (±1.01%)
Accuracy for k=32: 66.54% (±0.89%)
在讨论上述结果之前,我们先绘制支持集中示例数量与准确率的关系图:
def plot_few_shot(acc_dict, name, color=None, ax=None):
sns.set()
if ax is None:
fig, ax = plt.subplots(1,1,figsize=(5,3))
ks = sorted(list(acc_dict.keys()))
mean_accs = [acc_dict[k][0] for k in ks]
std_accs = [acc_dict[k][1] for k in ks]
ax.plot(ks, mean_accs, marker='o', markeredgecolor='k', markersize=6, label=name, color=color)
ax.fill_between(ks, [m-s for m,s in zip(mean_accs, std_accs)], [m+s for m,s in zip(mean_accs, std_accs)], alpha=0.2, color=color)
ax.set_xticks(ks)
ax.set_xlim([ks[0]-1, ks[-1]+1])
ax.set_xlabel("Number of shots per class", weight='bold')
ax.set_ylabel("Accuracy", weight='bold')
if len(ax.get_title()) == 0:
ax.set_title("Few-Shot Performance " + name, weight='bold')
else:
ax.set_title(ax.get_title() + " and " + name, weight='bold')
ax.legend()
return ax
ax = plot_few_shot(protonet_accuracies, name="ProtoNet", color="C1")
plt.show()
plt.close()
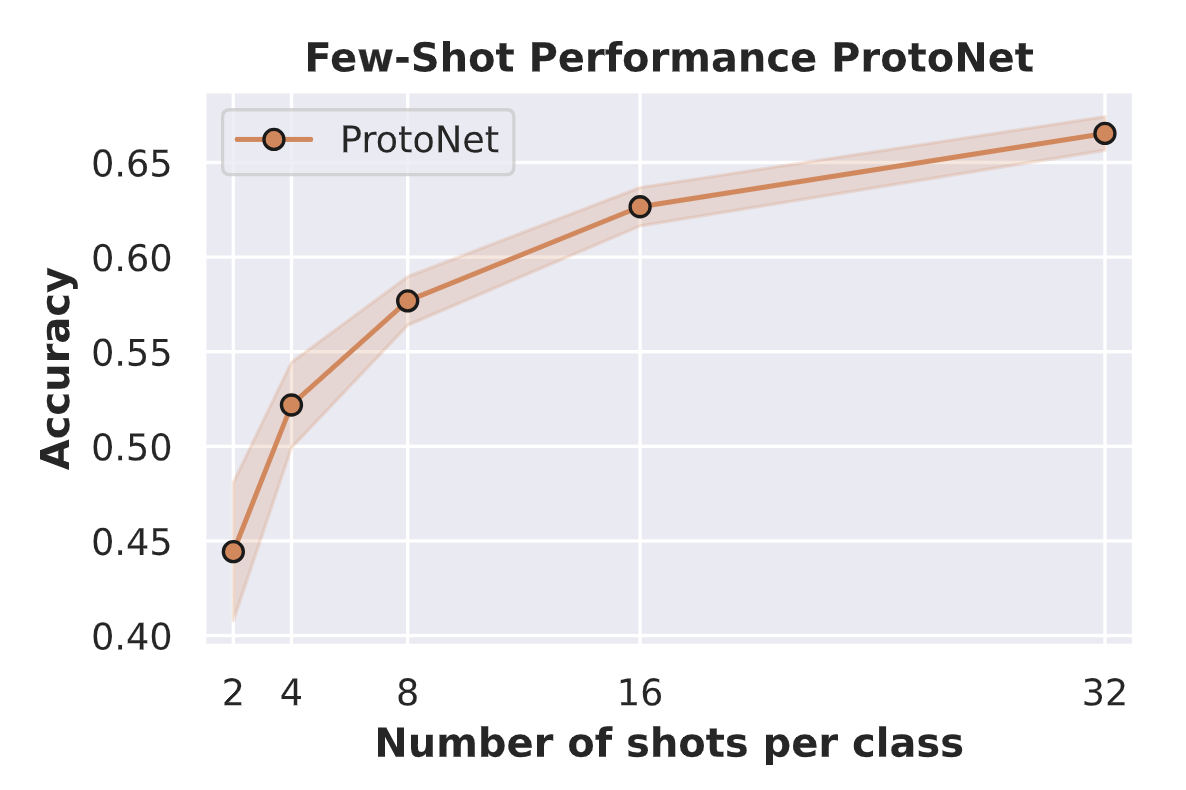
正如我们最初所预期的,ProtoNet 的性能确实随着我们拥有的样本数量增加而提高。然而,即使每个类别只有两个样本,我们的分类准确率也接近随机准确率(10%)的两倍。曲线显示出一种指数衰减的趋势,这意味着在 k = 2 k = 2 k=2 时增加两个额外的示例,其影响远大于在 k = 16 k = 16 k=16 时增加两个额外的示例。尽管如此,我们可以说 ProtoNet 能够相当好地适应新类别。
1.4 MAML 和 ProtoMAML
我们将探讨的第二种元学习算法是 MAML,即模型无关元学习。MAML 是一种基于优化的元学习算法,这意味着它试图将标准优化程序调整到少样本设置中。MAML 的思想相对简单:在训练期间,给定一个模型、支持集和查询集,我们在支持集上对模型进行 m m m 步优化,并评估查询损失相对于原始模型参数的梯度。对于同一个模型,我们对几个不同的支持集 - 查询集对执行此操作并累积梯度。这有助于学习一个能够快速适应训练任务的模型初始化。如果我们用 θ \theta θ 表示模型参数,我们可以将该过程可视化如下。

图4:参数初始化过程
MAML 的完整算法如下。在每个训练步骤中,我们采样一批任务,即一批支持集 - 查询集对。对于每个任务 T i \mathcal{T}_i Ti,我们在支持集上通过 SGD 对模型 f θ f_{\theta} fθ 进行优化,并将此模型表示为 f θ i ′ f_{\theta_i'} fθi′。我们将此优化称为内循环。使用这个新模型,我们计算原始参数 θ \theta θ 在查询集上的损失梯度。这些梯度在所有任务中累积并用于更新 θ \theta θ。这被称为外循环,因为我们遍历任务。MAML 的完整算法总结如下。

图5:MAML完整算法总结
为了从优化后的模型 f θ i ′ f_{\theta_i'} fθi′ 获得初始参数 θ \theta θ 的梯度,我们实际上需要二阶梯度,即梯度的梯度,因为支持集的梯度也依赖于 θ \theta θ。这使得 MAML 在计算上非常昂贵,尤其是当使用多个内循环步骤时。一个更简单但几乎同样有效的替代方案是一阶 MAML(FOMAML),它仅使用一阶梯度。这意味着忽略二阶梯度,我们可以通过计算相对于 θ i ′ \theta_i' θi′ 的梯度并将它们用作 θ \theta θ 的更新来简单地计算外循环梯度(算法 2 的第 10 行)。因此,新的更新规则变为:
θ ← θ − β ∑ T i ∼ p ( T ) ∇ θ i ′ L T i ( f θ i ′ ) \theta \leftarrow \theta - \beta \sum_{\mathcal{T}_i \sim p(\mathcal{T})} \nabla_{\theta_i'} \mathcal{L}_{\mathcal{T}_i}(f_{\theta_i'}) θ←θ−βTi∼p(T)∑∇θi′LTi(fθi′)
请注意,梯度符号中的 θ \theta θ 改为了 θ i ′ \theta_i' θi′。
1.4.1 ProtoMAML
MAML 的一个问题是如何设计输出分类层。如果所有任务都有不同数量的类别,我们可能需要在每次迭代中用零或随机值初始化输出层。即使类别数始终相同,我们也只是从随机预测开始。这需要几个内循环步骤才能达到合理的分类结果。为了克服这个问题,Triantafillou 等提出结合原型网络和 MAML 的优点。具体而言,我们可以使用原型来初始化输出层,以获得强大的初始化效果。研究表明,欧几里得距离上的 softmax 可以重新表述为带 softmax 的线性层。为此,我们首先写出新数据点 x ∗ \mathbf{x}^{*} x∗ 的特征向量 f θ ( x ∗ ) f_{\theta}(\mathbf{x}^{*}) fθ(x∗) 与类别 c c c 的原型 v c \mathbf{v}_c vc 之间的负欧几里得距离:
− ∣ ∣ f θ ( x ∗ ) − v c ∣ ∣ 2 = − f θ ( x ∗ ) T f θ ( x ∗ ) + 2 v c T f θ ( x ∗ ) − v c T v c -||f_{\theta}(\mathbf{x}^{*}) - \mathbf{v}_c||^2 = -f_{\theta}(\mathbf{x}^{*})^T f_{\theta}(\mathbf{x}^{*}) + 2 \mathbf{v}_c^{T} f_{\theta}(\mathbf{x}^{*}) - \mathbf{v}_c^T \mathbf{v}_c −∣∣fθ(x∗)−vc∣∣2=−fθ(x∗)Tfθ(x∗)+2vcTfθ(x∗)−vcTvc
我们在所有类别 c ∈ C c \in \mathcal{C} c∈C 上进行分类,并对距离进行 softmax。因此,任何对所有类别相同的项都可以在不改变输出概率的情况下移除。在上述方程中, − f θ ( x ∗ ) T f θ ( x ∗ ) -f_{\theta}(\mathbf{x}^{*})^T f_{\theta}(\mathbf{x}^{*}) −fθ(x∗)Tfθ(x∗) 就是这种情况,因为它与任何类别原型无关。因此,我们可以写成:
− ∣ ∣ f θ ( x ∗ ) − v c ∣ ∣ 2 = 2 v c T f θ ( x ∗ ) − ∣ ∣ v c ∣ ∣ 2 + constant -||f_{\theta}(\mathbf{x}^{*}) - \mathbf{v}_c||^2 = 2 \mathbf{v}_c^{T} f_{\theta}(\mathbf{x}^{*}) - ||\mathbf{v}_c||^2 + \text{constant} −∣∣fθ(x∗)−vc∣∣2=2vcTfθ(x∗)−∣∣vc∣∣2+constant
再次审视上述方程,它看起来很像一个线性层。为此,我们使用 W c , ⋅ = 2 v c \mathbf{W}_{c,\cdot} = 2 \mathbf{v}_c Wc,⋅=2vc 和 b c = − ∣ ∣ v c ∣ ∣ 2 b_c = -||\mathbf{v}_c||^2 bc=−∣∣vc∣∣2,这为我们提供了线性层 W f θ ( x ∗ ) + b \mathbf{W} f_{\theta}(\mathbf{x}^{*}) + \mathbf{b} Wfθ(x∗)+b。因此,如果我们用两倍的原型初始化输出权重,并用原型的负平方 L2 范数初始化偏置,我们就开始了一个原型网络。MAML 允许我们进一步适应这一层和网络的其余部分。
在接下来的内容中,我们将为少样本分类实现一阶 ProtoMAML。MAML 的实现除了输出层初始化外,其他都相同。
1.4.2 ProtoMAML 的实现
在实现 ProtoMAML 时,我们可以参考算法 2 并进行少量修改。在每个训练步骤中,我们首先采样一批任务,并为每个任务采样支持集和查询集。在我们的少样本分类案例中,这意味着我们只需从采样器中采样多个支持集 - 查询集对。对于每个任务,我们在支持集上微调当前模型。然而,由于我们需要记住原始参数以用于其他任务的外循环梯度更新和未来的训练步骤,我们需要创建模型的一个副本并仅微调副本。我们可以通过 Python 的标准函数如 deepcopy 来复制模型。内循环在下面 PyTorch Lightning 模块的 adapt_few_shot 函数中实现。
微调模型后,我们将其应用于查询集,并计算相对于原始参数 $ \theta $ 的一阶梯度。与简单的 MAML 不同,我们还需要考虑输出层初始化的梯度,即原型,因为它们直接依赖于 $ \theta $。为了高效地实现这一点,我们采取两个步骤。首先,我们通过将原始模型(而不是复制的模型)应用于支持元素来计算原型。在初始化输出层时,我们分离原型以阻止梯度。这是因为在内循环本身中,我们不想考虑通过原型回传到原始模型的梯度。然而,在内循环完成后,我们通过编写 output_weight = (output_weight - init_weight).detach() + init_weight 重新连接原型的计算图。虽然这一行没有改变变量 output_weight 的值,但它增加了其对原型初始化 init_weight 的依赖。因此,如果我们在 output_weight 上调用 .backward,我们将自动计算原始模型中原型初始化的一阶梯度。
在原始模型中计算所有梯度并将它们相加后,我们可以执行标准的优化步骤。然而,PyTorch Lightning 的方法旨在返回一个损失张量,我们首先在其上调用 .backward。由于这在这里不可能,我们需要自行执行优化步骤。所有详细信息可以在下面的代码中找到。
class ProtoMAML(pl.LightningModule):
def __init__(self, proto_dim, lr, lr_inner, lr_output, num_inner_steps):
"""
输入
proto_dim - 原型特征空间的维度
lr - 外循环 Adam 优化器的学习率
lr_inner - 内循环 SGD 优化器的学习率
lr_output - 内循环输出层的学习率
num_inner_steps - 要执行的内循环更新次数
"""
super().__init__()
self.save_hyperparameters()
self.model = get_convnet(output_size=self.hparams.proto_dim)
def configure_optimizers(self):
optimizer = optim.AdamW(self.parameters(), lr=self.hparams.lr)
scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[140,180], gamma=0.1)
return [optimizer], [scheduler]
def run_model(self, local_model, output_weight, output_bias, imgs, labels):
# 使用给定的输出层权重和输入执行模型
feats = local_model(imgs)
preds = F.linear(feats, output_weight, output_bias)
loss = F.cross_entropy(preds, labels)
acc = (preds.argmax(dim=1) == labels).float()
return loss, preds, acc
def adapt_few_shot(self, support_imgs, support_targets):
# 确定原型初始化
support_feats = self.model(support_imgs)
prototypes, classes = ProtoNet.calculate_prototypes(support_feats, support_targets)
support_labels = (classes[None,:] == support_targets[:,None]).long().argmax(dim=-1)
# 创建内循环模型和优化器
local_model = deepcopy(self.model)
local_model.train()
local_optim = optim.SGD(local_model.parameters(), lr=self.hparams.lr_inner)
local_optim.zero_grad()
# 使用基于原型的初始化创建输出层权重
init_weight = 2 * prototypes
init_bias = -torch.norm(prototypes, dim=1)**2
output_weight = init_weight.detach().requires_grad_()
output_bias = init_bias.detach().requires_grad_()
# 在支持集上优化内循环模型
for _ in range(self.hparams.num_inner_steps):
# 确定支持集上的损失
loss, _, _ = self.run_model(local_model, output_weight, output_bias, support_imgs, support_labels)
# 计算梯度并执行内循环更新
loss.backward()
local_optim.step()
# 通过 SGD 更新输出层
with torch.no_grad():
output_weight.copy_(output_weight - self.hparams.lr_output * output_weight.grad)
output_bias.copy_(output_bias - self.hparams.lr_output * output_bias.grad)
# 重置梯度
local_optim.zero_grad()
output_weight.grad.fill_(0)
output_bias.grad.fill_(0)
# 重新附上原型的计算图
output_weight = (output_weight - init_weight).detach() + init_weight
output_bias = (output_bias - init_bias).detach() + init_bias
return local_model, output_weight, output_bias, classes
def outer_loop(self, batch, mode="train"):
accuracies = []
losses = []
self.model.zero_grad()
# 确定任务批次的梯度
for task_batch in batch:
imgs, targets = task_batch
support_imgs, query_imgs, support_targets, query_targets = split_batch(imgs, targets)
# 执行内循环适应
local_model, output_weight, output_bias, classes = self.adapt_few_shot(support_imgs, support_targets)
# 确定查询集的损失
query_labels = (classes[None,:] == query_targets[:,None]).long().argmax(dim=-1)
loss, preds, acc = self.run_model(local_model, output_weight, output_bias, query_imgs, query_labels)
# 计算查询集损失的梯度
if mode == "train":
loss.backward()
for p_global, p_local in zip(self.model.parameters(), local_model.parameters()):
p_global.grad += p_local.grad # 一阶近似 -> 添加微调模型和基础模型的梯度
accuracies.append(acc.mean().detach())
losses.append(loss.detach())
# 更新基础模型
if mode == "train":
opt = self.optimizers()
opt.step()
opt.zero_grad()
self.log(f"{mode}_loss", sum(losses) / len(losses))
self.log(f"{mode}_acc", sum(accuracies) / len(accuracies))
def training_step(self, batch, batch_idx):
self.outer_loop(batch, mode="train")
return None # 返回 None 意味着我们跳过 PyTorch Lightning 的默认训练优化步骤
def validation_step(self, batch, batch_idx):
# 验证需要微调模型,因此需要启用梯度
torch.set_grad_enabled(True)
self.outer_loop(batch, mode="val")
torch.set_grad_enabled(False)
1.4.3 ProtoMAML模型训练
为了训练 ProtoMAML,我们需要稍微改变采样方式。我们不再使用单个支持集-查询集批次,而是需要采样多个。为此,我们使用另一种采样器,它从 FewShotBatchSampler 中组合多个批次并在之后返回。此外,我们为数据加载器定义了一个 collate_fn,它接收支持集-查询集图像堆叠并以列表形式返回任务。这使得在 PyTorch Lightning 模块中处理变得更加容易。采样器的实现如下。
class TaskBatchSampler(object):
def __init__(self, dataset_targets, batch_size, N_way, K_shot, include_query=False, shuffle=True):
"""
输入:
dataset_targets - PyTorch 张量,表示数据元素的标签。
batch_size - 每个批次中要聚合的任务数
N_way - 每个批次中要采样的类别数。
K_shot - 每个类别中要采样的示例数。
include_query - 如果为 True,则返回大小为 N_way*K_shot*2 的批次,可以拆分为支持集和查询集。简化了支持集和查询集采样相同类别但不同示例的实现。
shuffle - 如果为 True,则在每次迭代中重新打乱示例和类别(用于训练)
"""
super().__init__()
self.batch_sampler = FewShotBatchSampler(dataset_targets, N_way, K_shot, include_query, shuffle)
self.task_batch_size = batch_size
self.local_batch_size = self.batch_sampler.batch_size
def __iter__(self):
# 在返回索引之前聚合多个批次
batch_list = []
for batch_idx, batch in enumerate(self.batch_sampler):
batch_list.extend(batch)
if (batch_idx + 1) % self.task_batch_size == 0:
yield batch_list
batch_list = []
def __len__(self):
return len(self.batch_sampler) // self.task_batch_size
def get_collate_fn(self):
# 返回一个 collate 函数,将一个大张量转换为任务特定的张量列表
def collate_fn(item_list):
imgs = torch.stack([img for img, target in item_list], dim=0)
targets = torch.stack([target for img, target in item_list], dim=0)
imgs = imgs.chunk(self.task_batch_size, dim=0)
targets = targets.chunk(self.task_batch_size, dim=0)
return list(zip(imgs, targets))
return collate_fn
数据加载器的创建使用此采样器非常直接。请注意,由于训练批次需要加载许多图像,因此建议使用的进程数比平时少。
# 训练常量(与 ProtoNet 相同)
N_WAY = 5
K_SHOT = 4
# 训练集
train_protomaml_sampler = TaskBatchSampler(train_set.targets,
include_query=True,
N_way=N_WAY,
K_shot=K_SHOT,
batch_size=16)
train_protomaml_loader = data.DataLoader(train_set,
batch_sampler=train_protomaml_sampler,
collate_fn=train_protomaml_sampler.get_collate_fn(),
num_workers=2)
# 验证集
val_protomaml_sampler = TaskBatchSampler(val_set.targets,
include_query=True,
N_way=N_WAY,
K_shot=K_SHOT,
batch_size=1, # We do not update the parameters, hence the batch size is irrelevant here
shuffle=False)
val_protomaml_loader = data.DataLoader(val_set,
batch_sampler=val_protomaml_sampler,
collate_fn=val_protomaml_sampler.get_collate_fn(),
num_workers=2)
现在,我们已经准备好训练我们的 ProtoMAML 了。我们使用与 ProtoNet 相同的特征空间大小,但由于外循环梯度在 16 个批次上累积,因此可以使用更高的学习率。内循环学习率设置为 0.1,这比外循环学习率高得多,因为我们在内循环中使用 SGD 而不是 Adam。通常,如果基模型非常深或经过预训练,输出层的学习率会高于基模型。但在我们的设置中,我们观察到使用与基模型不同的学习率没有显著影响。内循环更新次数是另一个关键的超参数,它取决于我们训练任务的相似性。由于所有任务都基于同一数据集的图像,我们发现单次内循环更新在训练中实现的性能与 3 次或 5 次更新相似,但训练速度明显更快。然而,在强化学习和自然语言处理中,通常需要更多的内循环步骤。
protomaml_model = train_model(ProtoMAML,
proto_dim=64,
lr=1e-3,
lr_inner=0.1,
lr_output=0.1,
num_inner_steps=1, # 取值通常在 1 到 10 之间
train_loader=train_protomaml_loader,
val_loader=val_protomaml_loader)
让我们看看训练的 TensorBoard。
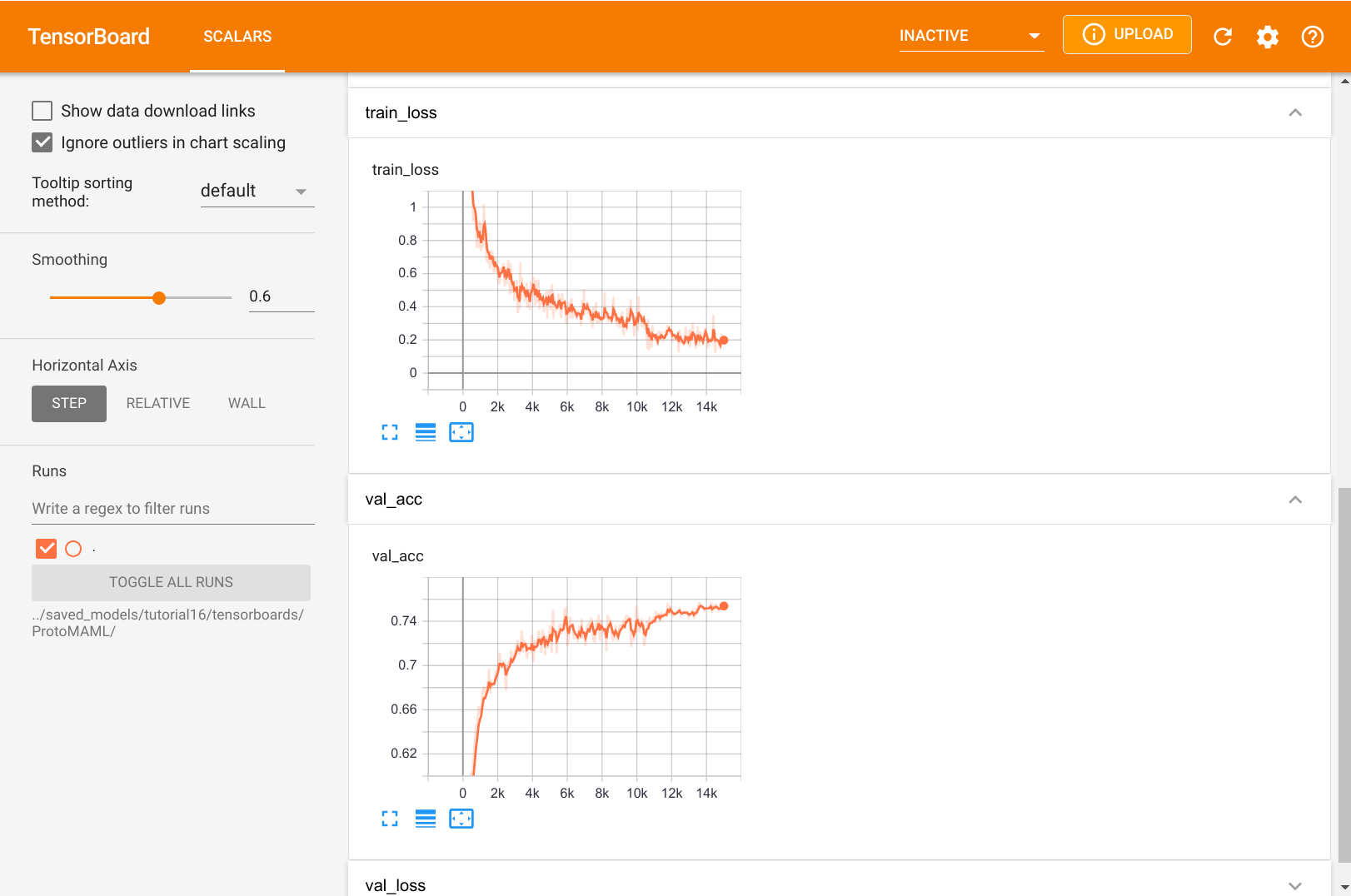
图6:ProtoMAML训练日志
与 ProtoNet 相比,一个明显的区别是损失曲线看起来噪音少得多。这是因为我们在多个任务上平均了外循环梯度,从而得到了更平滑的训练曲线。此外,在 200 个周期后,我们只有 15,000 次训练迭代。这再次是因为任务批次导致迭代次数减少了 16 倍。然而,在这个实验中,每次迭代都处理了 16 倍的数据量。因此,ProtoMAML 和 ProtoNet 之间的比较仍然是公平的。乍一看验证准确率,人们可能会认为 ProtoNet 的性能优于 ProtoMAML,但我们必须通过下面的测试来验证这一点。
1.4.4 ProtoMAML模型测试
我们以与测试 ProtoNet 相同的方式测试 ProtoMAML,即从测试集中随机选取示例作为支持集,并将数据集的其余部分用作查询集。与仅计算所有示例的原型不同,我们需要为每个支持集微调一个单独的模型。这就是为什么这个过程比 ProtoNet 更昂贵的原因。在我们的情况下,测试 k = { 2 , 4 , 8 , 16 , 32 } k = \{2, 4, 8, 16, 32\} k={2,4,8,16,32} 几乎需要一个小时。因此,我们除了预训练模型外,还提供了评估文件。
def test_protomaml(model, dataset, k_shot=4):
pl.seed_everything(42)
model = model.to(device)
num_classes = dataset.targets.unique().shape[0]
exmps_per_class = dataset.targets.shape[0] // num_classes
# 用于完整测试集作为查询集的数据加载器
full_dataloader = data.DataLoader(dataset,
batch_size=128,
num_workers=4,
shuffle=False,
drop_last=False)
# 用于采样支持集的数据加载器
sampler = FewShotBatchSampler(dataset.targets,
include_query=False,
N_way=num_classes,
K_shot=k_shot,
shuffle=False,
shuffle_once=False)
sample_dataloader = data.DataLoader(dataset,
batch_sampler=sampler,
num_workers=2)
# 我们以两种方式遍历整个数据集。首先,选择 k-shot 批次。
# 其次,在所有其他示例上评估模型
accuracies = []
for (support_imgs, support_targets), support_indices in tqdm(zip(sample_dataloader, sampler), "Performing few-shot finetuning"):
support_imgs = support_imgs.to(device)
support_targets = support_targets.to(device)
# 在支持集上微调新模型
local_model, output_weight, output_bias, classes = model.adapt_few_shot(support_imgs, support_targets)
with torch.no_grad(): # 查询集不需要梯度
local_model.eval()
batch_acc = torch.zeros((0,), dtype=torch.float32, device=device)
# 评估测试数据集中的所有示例
for query_imgs, query_targets in full_dataloader:
query_imgs = query_imgs.to(device)
query_targets = query_targets.to(device)
query_labels = (classes[None,:] == query_targets[:,None]).long().argmax(dim=-1)
_, _, acc = model.run_model(local_model, output_weight, output_bias, query_imgs, query_labels)
batch_acc = torch.cat([batch_acc, acc.detach()], dim=0)
# 排除支持集元素
for s_idx in support_indices:
batch_acc[s_idx] = 0
batch_acc = batch_acc.sum().item() / (batch_acc.shape[0] - len(support_indices))
accuracies.append(batch_acc)
return mean(accuracies), stdev(accuracies)
与训练相比,建议在测试期间使用更多的内循环更新。在训练期间,我们关注的不是从内循环中获得最佳模型,而是能够提供最佳梯度的模型。因此,训练中一次更新可能已经足够,但对于测试,通常观察到更多的更新次数可以显著提升性能。因此,我们在测试前将内循环更新次数改为 200 次。
protomaml_model.hparams.num_inner_steps = 200
现在,我们可以测试我们的模型。对于预训练模型,我们提供了一个 json 文件来减少评估时间。
protomaml_result_file = os.path.join(CHECKPOINT_PATH, "protomaml_fewshot.json")
if os.path.isfile(protomaml_result_file):
# 加载预计算的结果
with open(protomaml_result_file, 'r') as f:
protomaml_accuracies = json.load(f)
protomaml_accuracies = {int(k): v for k, v in protomaml_accuracies.items()}
else:
# 执行与 ProtoNet 相同的实验
protomaml_accuracies = dict()
for k in [2, 4, 8, 16, 32]:
protomaml_accuracies[k] = test_protomaml(protomaml_model, test_set, k_shot=k)
# 导出结果
with open(protomaml_result_file, 'w') as f:
json.dump(protomaml_accuracies, f, indent=4)
for k in protomaml_accuracies:
print(f"Accuracy for k={k}: {100.0*protomaml_accuracies[k][0]:4.2f}% (+-{100.0*protomaml_accuracies[k][1]:4.2f}%)")
out:
Accuracy for k=2: 42.89% (±3.82%)
Accuracy for k=4: 52.27% (±2.72%)
Accuracy for k=8: 59.23% (±1.50%)
Accuracy for k=16: 63.94% (±1.24%)
Accuracy for k=32: 67.57% (±0.90%)
同样,让我们在之前的图中绘制结果。
ax = plot_few_shot(protonet_accuracies, name="ProtoNet", color="C1")
plot_few_shot(protomaml_accuracies, name="ProtoMAML", color="C2", ax=ax)
plt.show()
plt.close()
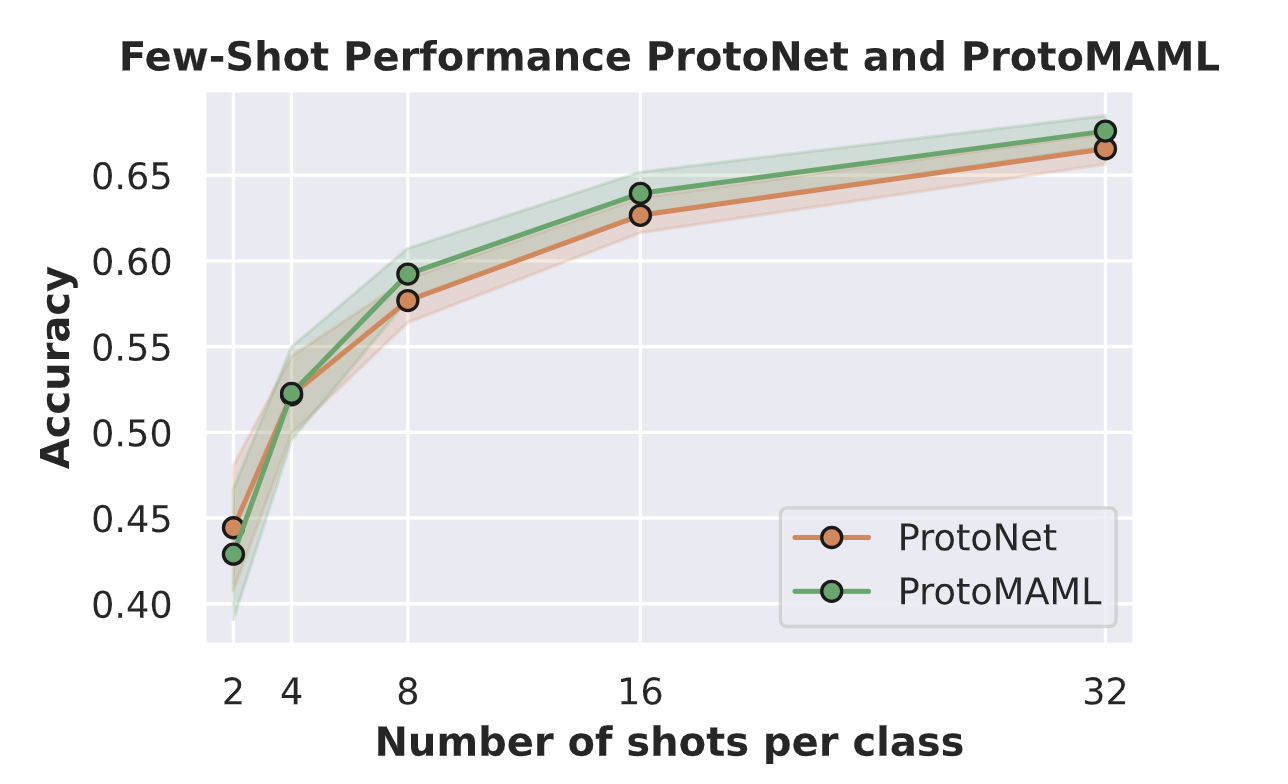
我们可以观察到,ProtoMAML 确实在 ( k > 4 ) 时能够超越 ProtoNet。这是因为,随着样本数量的增加,适应基模型参数变得更为重要。与此同时,对于 ( k = 2 ),ProtoMAML 的性能低于 ProtoNet。这可能与选择 200 次内循环更新有关,因为随着更新次数的增加,过拟合的风险也随之增加。尽管如此,( k = 2 ) 时的高标准差使得很难得出任何具有统计学意义的结论。
总体而言,我们可以得出结论,ProtoMAML 在较大的样本数量下略微优于 ProtoNet。然而,ProtoMAML 的一个缺点是其训练和测试时间更长。ProtoNet 提供了一个简单、高效且强大的基线,适用于资源有限的情况。
1.5 领域自适应
到目前为止,我们在训练模型所用的同一数据集上评估了我们的元学习算法。然而,当我们希望从一个数据集迁移到另一个数据集时,元学习算法尤其有趣。那么,如果我们在与 CIFAR 完全不同的数据集上应用它们会发生什么呢?下面我们将尝试这一点,并在 SVHN 数据集上评估 ProtoNet 和 ProtoMAML。
1.5.1 SVHN 数据集
街景门牌号(SVHN)数据集是一个用于门牌号检测的真实世界图像数据集。它与 MNIST 类似,包含 0 到 9 的类别,但由于其真实世界场景以及左右可能存在的干扰数字而更具挑战性。首先加载数据集,并可视化一些图像以了解其情况。
SVHN_test_dataset = SVHN(root=DATASET_PATH, split='test', download=False, transform=transforms.ToTensor())
# 可视化一些示例
NUM_IMAGES = 12
SVHN_images = torch.stack([SVHN_test_dataset[np.random.randint(len(SVHN_test_dataset))][0] for idx in range(NUM_IMAGES)], dim=0)
img_grid = torchvision.utils.make_grid(SVHN_images, nrow=6, normalize=True, pad_value=0.9)
img_grid = img_grid.permute(1, 2, 0)
plt.figure(figsize=(8,8))
plt.title("Image examples of the SVHN dataset")
plt.imshow(img_grid)
plt.axis('off')
plt.show()
plt.close()

每张图像都标有 0 到 9 之间的类别,表示图像中的主要数字。我们的 ProtoNet 和 ProtoMAML 能否仅从少量示例中学习对数字进行分类?这正是我们将在下面进行测试的内容。由于图像尺寸与 CIFAR 相同,因此我们可以直接使用这些图像。我们首先准备数据集,为此我们选取每个类别的前 500 张图像。对于此数据集,我们使用之前的测试函数来估计不同样本数量下的性能。
imgs = np.transpose(SVHN_test_dataset.data, (0,2,3,1))
targets = SVHN_test_dataset.labels
min_label_count = min(500, np.bincount(SVHN_test_dataset.labels).min()) # 限制示例数量为 500 以减少测试时间
idxs = np.concatenate([np.where(targets==c)[0][:min_label_count] for c in range(1+targets.max())], axis=0)
imgs = imgs[idxs]
targets = torch.from_numpy(targets[idxs]).long()
svhn_fewshot_dataset = ImageDataset(imgs, targets, img_transform=test_transform)
svhn_fewshot_dataset.imgs.shape
out:
(5000, 32, 32, 3)
1.5.2 对比实验
首先,我们可以将 ProtoNet 应用于 SVHN 数据集:
protonet_svhn_accuracies = dict()
data_feats = None
for k in [2, 4, 8, 16, 32]:
protonet_svhn_accuracies[k], data_feats = test_proto_net(protonet_model, svhn_fewshot_dataset, data_feats=data_feats, k_shot=k)
print(f"Accuracy for k={k}: {100.0*protonet_svhn_accuracies[k][0]:4.2f}% (+-{100*protonet_svhn_accuracies[k][1]:4.2f}%)")
out:
Accuracy for k=2: 18.79% (±2.27%)
Accuracy for k=4: 21.89% (±2.06%)
Accuracy for k=8: 25.55% (±1.78%)
Accuracy for k=16: 29.02% (±1.83%)
Accuracy for k=32: 32.88% (±1.33%)
结果表明,性能远低于 CIFAR 上的结果,当 ( k = 2 ) 时仅略高于随机水平。那么 ProtoMAML 呢?我们同样提供了评估文件,因为评估可能需要几分钟才能完成。
protomaml_result_file = os.path.join(CHECKPOINT_PATH, "protomaml_svhn_fewshot.json")
if os.path.isfile(protomaml_result_file):
# 加载预计算的结果
with open(protomaml_result_file, 'r') as f:
protomaml_svhn_accuracies = json.load(f)
protomaml_svhn_accuracies = {int(k): v for k, v in protomaml_svhn_accuracies.items()}
else:
# 执行与 ProtoNet 相同的实验
protomaml_svhn_accuracies = dict()
for k in [2, 4, 8, 16, 32]:
protomaml_svhn_accuracies[k] = test_protomaml(protomaml_model, svhn_fewshot_dataset, k_shot=k)
# 导出结果
with open(protomaml_result_file, 'w') as f:
json.dump(protomaml_svhn_accuracies, f, indent=4)
for k in protomaml_svhn_accuracies:
print(f"Accuracy for k={k}: {100.0*protomaml_svhn_accuracies[k][0]:4.2f}% (+-{100.0*protomaml_svhn_accuracies[k][1]:4.2f}%)")
Out:
Accuracy for k=2: 17.11% (±1.95%)
Accuracy for k=4: 21.29% (±1.92%)
Accuracy for k=8: 27.62% (±1.84%)
Accuracy for k=16: 36.17% (±1.80%)
Accuracy for k=32: 46.03% (±1.65%)
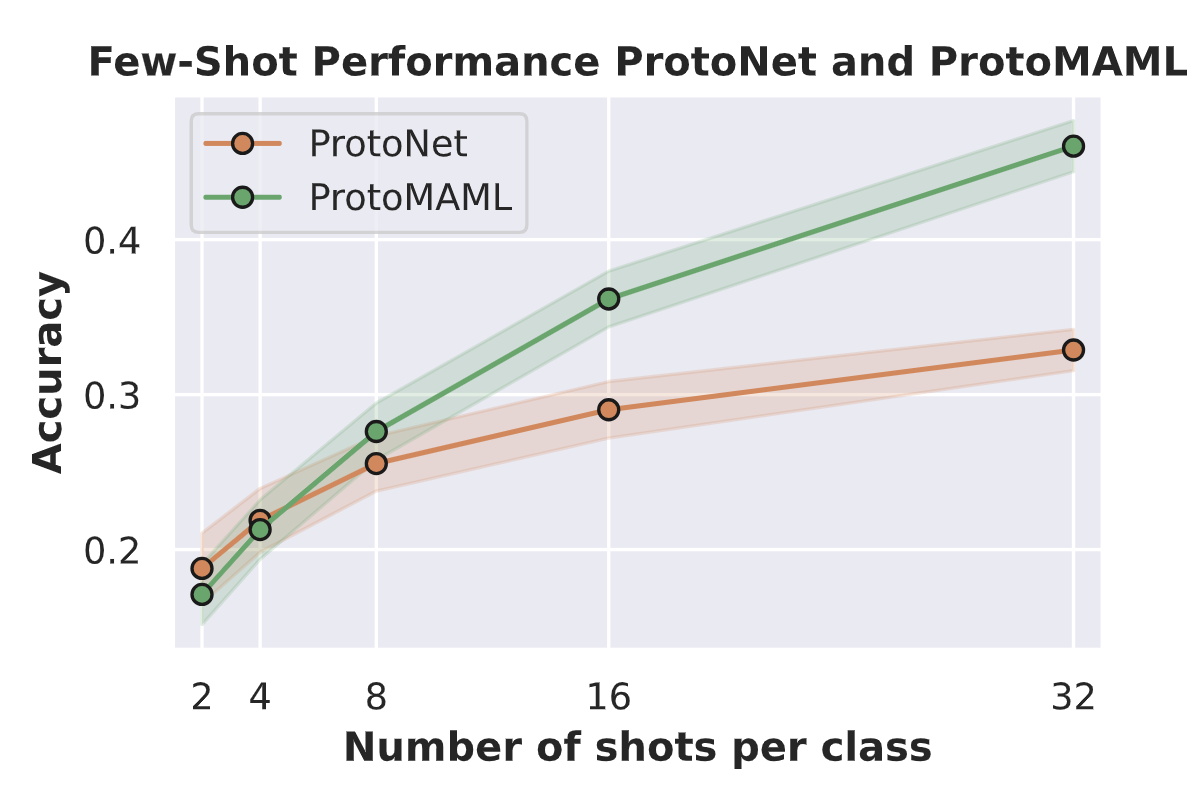
当 k ≤ 4 k\leq 4 k≤4 时,ProtoMAML 的性能与 ProtoNet 相当,但对于超过 8 个样本的情况,ProtoMAML 的性能显著优于 ProtoNet。这表明我们可以适应基模型,这在数据与原始训练数据不匹配时至关重要。当 k = 32 k = 32 k=32 时,ProtoMAML 的分类准确率比 ProtoNet 高出 13%,而 ProtoNet 的性能已经开始趋于平稳。我们可以在下面的图表中更清晰地看到这一趋势。
ax = plot_few_shot(protonet_svhn_accuracies, name="ProtoNet", color="C1")
plot_few_shot(protomaml_svhn_accuracies, name="ProtoMAML", color="C2", ax=ax)
plt.show()
plt.close()
- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用
 ProtoNet与ProtoMAML元学习实践
ProtoNet与ProtoMAML元学习实践























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








