- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用
用于图像建模的归一化流
学习目标
在本课程中,我们将仔细研究复杂、深入的归一化流。深度归一化流当前最流行的应用是对图像数据集进行建模。至于其他生成模型,图像是一个很好的开始研究的领域,因为 CNN 被广泛研究并且存在强大的模型,图像是高维和复杂的,以及图像是离散整数。在本课程中,我们将回顾图像建模的归一化流的当前进展,并获得编码归一化流的实践经验。
相关知识点
- 用于图像建模的归一化流
学习内容
1 用于图像建模的归一化流
1.1 实验前准备
# 安装依赖
%pip install seaborn
%pip install --upgrade jupyter ipywidgets
%pip install --upgrade ipywidgets
%pip install tabulate
%pip install ipdb
无NPU硬件环境的无需下载下列资源。
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_codes/8843e7ee45cb11f08c19fa163edcddae/ascend_npu_for_pytorch_lightning.zip
!unzip ascend_npu_for_pytorch_lightning.zip
%cd ascend_npu_for_pytorch_lightning
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/c02b287e324a11f0937ef8fe5e46a8fb/data.zip
!unzip data.zip
## 标准库
import os
import math
import time
import numpy as np
## 用于绘图的导入
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf')
from matplotlib.colors import to_rgb
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2.0
import seaborn as sns
sns.reset_orig()
## 进度条
from tqdm.notebook import tqdm
## PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import Subset, DataLoader
# Torchvision
import torchvision
from torchvision.datasets import MNIST
from torchvision import transforms
# PyTorch Lightning
try:
import pytorch_lightning as pl
except ModuleNotFoundError:
%pip install --quiet pytorch-lightning>=1.4
import pytorch_lightning as pl
from pytorch_lightning.callbacks import LearningRateMonitor, ModelCheckpoint
# 数据集所在文件夹的路径,或者是数据集应该被下载到的文件夹路径(例如 MNIST 数据集)。
DATASET_PATH = "./data"
# 预训练模型保存的文件夹路径
CHECKPOINT_PATH = "./models"
# 设置随机种子
pl.seed_everything(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# 获取本实验将全程使用的设备
device = torch.device("cpu") if not torch.npu.is_available() else torch.device("npu:0")
print("Using device", device)
同样,我们有一些预训练模型。我们将在本课程中使用 MNIST 数据集。尽管 MNIST 很简单,但它对小型生成模型来说也是一个挑战,因为它需要对图像的整体理解。同时,我们可以很容易地判断生成的图像是否来自与数据集相同的分布(即表示真实数字)。
为了更好地处理图像的离散性,我们将它们从 0-1 的范围转换为 0-255 的范围作为整数。
# 将图像像素值从 0 - 1 的范围转换为 0 - 255 的整数范围。
def discretize(sample):
return (sample * 255).to(torch.int32)
# 对每张图像应用变换操作 => 将它们转换为张量并进行离散化处理
transform = transforms.Compose([transforms.ToTensor(),
discretize])
# 正在加载训练数据集。我们需要将其划分为训练集和验证集两部分。
train_dataset = MNIST(root=DATASET_PATH, train=True, transform=transform, download=False)
# 正在加载测试集
test_set = MNIST(root=DATASET_PATH, train=False, transform=transform, download=False)
pl.seed_everything(42)
# 定义要使用的训练和测试数据的数量
reduced_train_size = 1000 # 减少后的训练数据量
reduced_test_size = 200 # 减少后的测试数据量
# 定义要划分的训练集和验证集的数量
train_size = 800 # 划分后的训练集数量
val_size = 200 # 划分后的验证集数量
#train_set, val_set = torch.utils.data.random_split(train_dataset, [50000, 10000])
# 创建训练数据集的子集
reduced_train_dataset = Subset(train_dataset, indices=range(reduced_train_size))
# 将减少后的训练数据集划分为训练集和验证集
train_set, val_set = torch.utils.data.random_split(reduced_train_dataset, [train_size, val_size])
# 创建测试数据集的子集
test_set = Subset(test_set, indices=range(reduced_test_size))
# 我们定义一组数据加载器,以便后续能用于各种不同的用途。
# 请注意,在实际训练模型时,我们会使用批次大小更小的不同数据加载器。
train_loader = data.DataLoader(train_set, batch_size=256, shuffle=False, drop_last=False)
val_loader = data.DataLoader(val_set, batch_size=64, shuffle=False, drop_last=False, num_workers=4)
test_loader = data.DataLoader(test_set, batch_size=64, shuffle=False, drop_last=False, num_workers=4)
# 验证加载结果
print(f"原始训练集大小: {len(train_dataset)}")
print(f"缩减后训练集大小: {len(train_set)}")
print(f"测试集大小: {len(test_set)}")
# 显示第一个样本
image, label = train_dataset[0]
print(f"样本形状: {image.shape}, 标签: {label}")
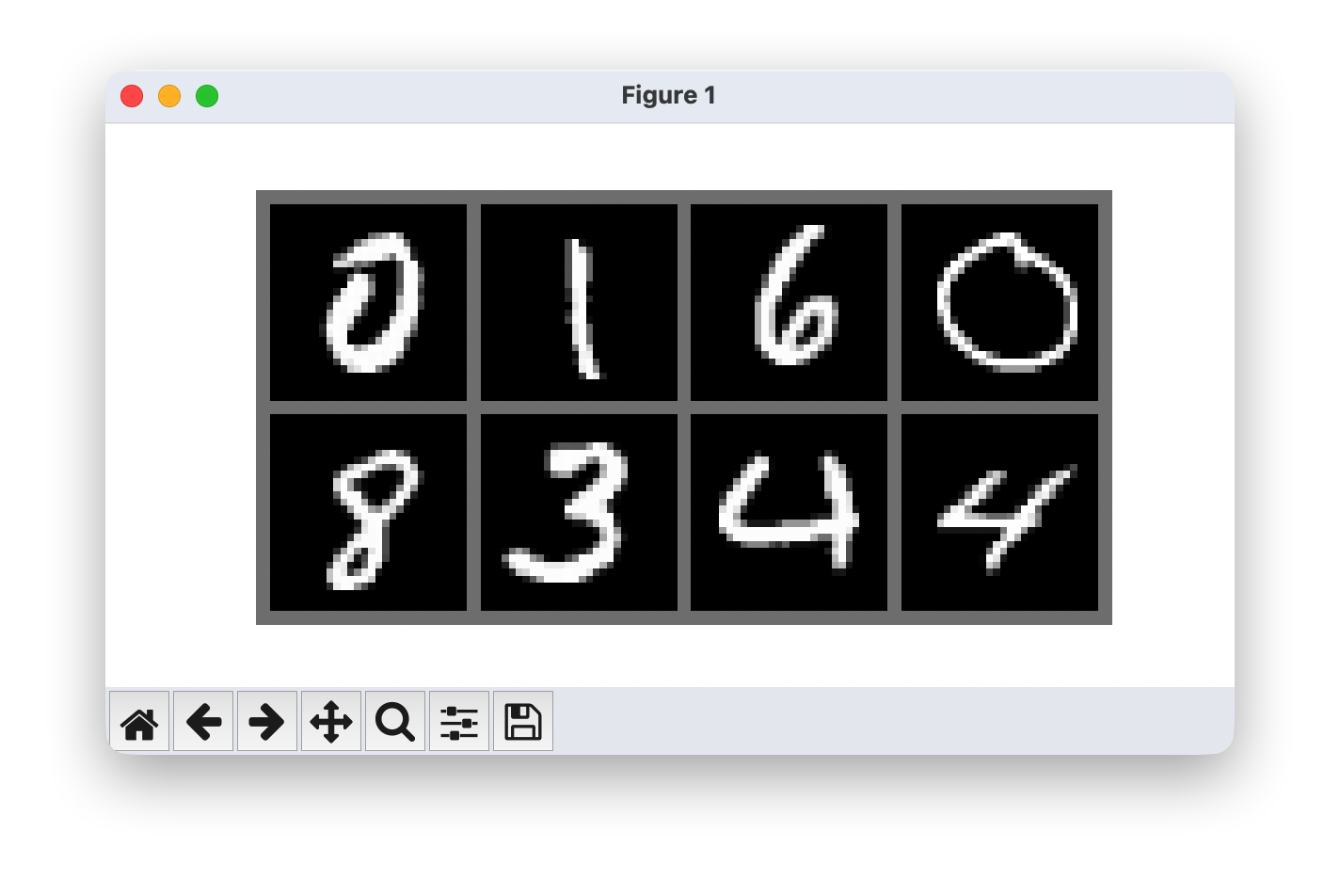
此外,我们将在下面定义一个函数来简化图像/样本的可视化。MNIST 数据集的一些训练示例如下所示。
def show_imgs(imgs, title=None, row_size=4):
# 创建一个图片网格(我们最多使用 8 列)。
num_imgs = imgs.shape[0] if isinstance(imgs, torch.Tensor) else len(imgs)
is_int = imgs.dtype==torch.int32 if isinstance(imgs, torch.Tensor) else imgs[0].dtype==torch.int32
nrow = min(num_imgs, row_size)
ncol = int(math.ceil(num_imgs/nrow))
imgs = torchvision.utils.make_grid(imgs, nrow=nrow, pad_value=128 if is_int else 0.5)
np_imgs = imgs.cpu().numpy()
# 绘制图片网格
plt.figure(figsize=(1.5*nrow, 1.5*ncol))
plt.imshow(np.transpose(np_imgs, (1,2,0)), interpolation='nearest')
plt.axis('off')
if title is not None:
plt.title(title)
plt.show()
plt.close()
show_imgs([train_set[i][0] for i in range(8)])
1.2 Flows 适配图像生成模型的归一化处理
诸如基于Energy的模型、变分自动编码器 (VAE) 和生成对抗网络 (GAN) 作为生成模型,它们都没有明确学习实际输入数据的概率密度函数 p ( x ) p(x) p(x)。虽然 VAE 对下限进行建模,但基于Energy的模型仅隐式学习概率密度。另一方面,GAN 为我们提供了一种生成新数据的采样机制,而不提供可能性估计。我们在这里要看的生成模型称为 Normalizing Flows,它实际上模拟了真实的数据分布 p ( x ) p(x) p(x) ,并为我们提供了精确的似然估计。下面,我们可以直观地比较 VAE、GAN 和 Flows:
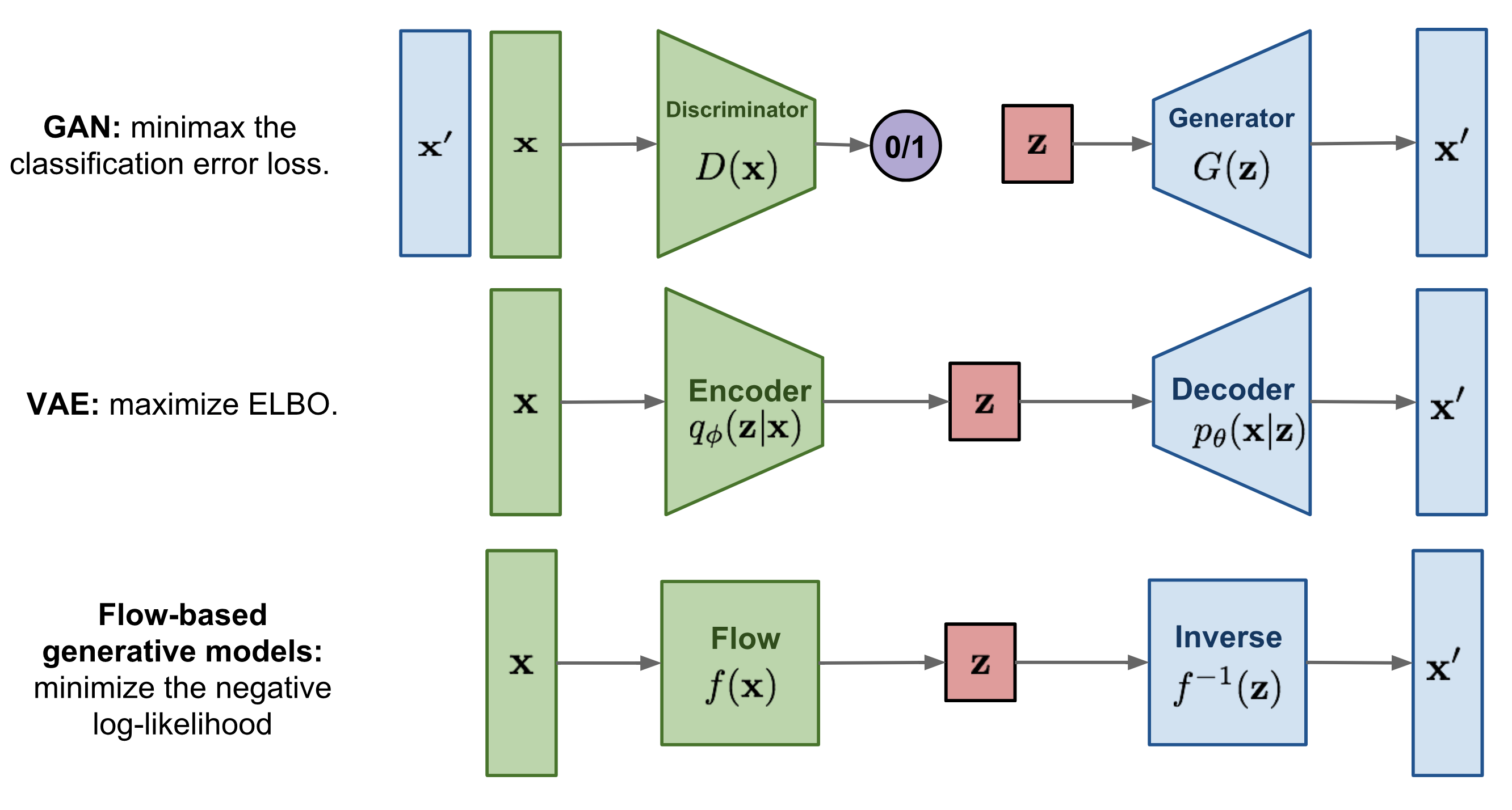
与变分自编码器(VAEs)相比,主要区别在于流模型使用可逆函数 f f f 将输入数据映射到 x x x 潜在表示。为实现这一点, z z z 必须具有与 x x x 相同的形状 。这与变分自编码器不同,在变分自编码器中, z z z 的维度通常比原始输入数据低得多。然而,可逆映射也意味着对于每个数据点 x x x,都有一个对应的潜在表示 z z z,这使我们能够进行无损重建(从 z z z到 x x x)。在上面的可视化中,这意味着 x = x ′ x=x' x=x′,对于流模型而言,无论选择何种可逆函数 f f f和输入 x x x,我们都可以确定 p ( x ) p(x) p(x)。
尽管如此,归一化流是如何通过可逆函数对概率密度进行建模的呢?这个问题的答案在于变量变换规则。具体来说,给定一个先验密度 p z ( z ) p_z(z) pz(z)(例如高斯分布)以及一个可逆函数 f f f,我们可以按如下方式确定 p x ( x ) p_x(x) px(x):
∫ p x ( x ) d x = ∫ p z ( z ) d z = 1 (by definition of a probability distribution) ⇔ p x ( x ) = p z ( z ) ∣ d z d x ∣ = p z ( f ( x ) ) ∣ d f ( x ) d x ∣ \begin{split} \int p_x(x) dx & = \int p_z(z) dz = 1 \hspace{1cm}\text{(by definition of a probability distribution)}\\ \Leftrightarrow p_x(x) & = p_z(z) \left|\frac{dz}{dx}\right| = p_z(f(x)) \left|\frac{df(x)}{dx}\right| \end{split} ∫px(x)dx⇔px(x)=∫pz(z)dz=1(by definition of a probability distribution)=pz(z) dxdz =pz(f(x)) dxdf(x)
因此,为了确定 x x x的概率,我们只需要确定它在潜在空间中的概率,并求出的导数 f f f。请注意,这是针对单变量分布的情况,并且 f f f要求是可逆且光滑的。对于多变量的情况,导数就变成了雅可比矩阵,我们需要取其行列式。由于我们通常使用对数似然作为目标函数,下面我们用对数形式写出多变量的表达式:
log p x ( x ) = log p z ( f ( x ) ) + log ∣ det d f ( x ) d x ∣ \log p_x(\mathbf{x}) = \log p_z(f(\mathbf{x})) + \log{} \left|\det \frac{df(\mathbf{x})}{d\mathbf{x}}\right| logpx(x)=logpz(f(x))+log detdxdf(x)
虽然我们现在知道了归一化流是如何得到其似然的,但从直观上看,归一化流究竟起什么作用可能仍不明确。为此,我们应该从流的逆过程角度来看,从先验概率密度 p z ( z ) p_z(z) pz(z)开始。如果我们对它应用一个可逆函数,实际上就是 “变换” 它的概率密度。例如,如果 f − 1 ( z ) = z + 1 f^{-1}(z)=z+1 f−1(z)=z+1,我们将密度平移了一个单位,同时它仍然是一个有效的概率分布,并且是可逆的。我们还可以应用更复杂的变换,比如缩放 f − 1 ( z ) = 2 z + 1 f^{-1}(z)=2z+1 f−1(z)=2z+1:,但这里你可能会看到一些不同。当进行缩放时,你也改变了概率密度的 “体积”,例如在均匀分布上:
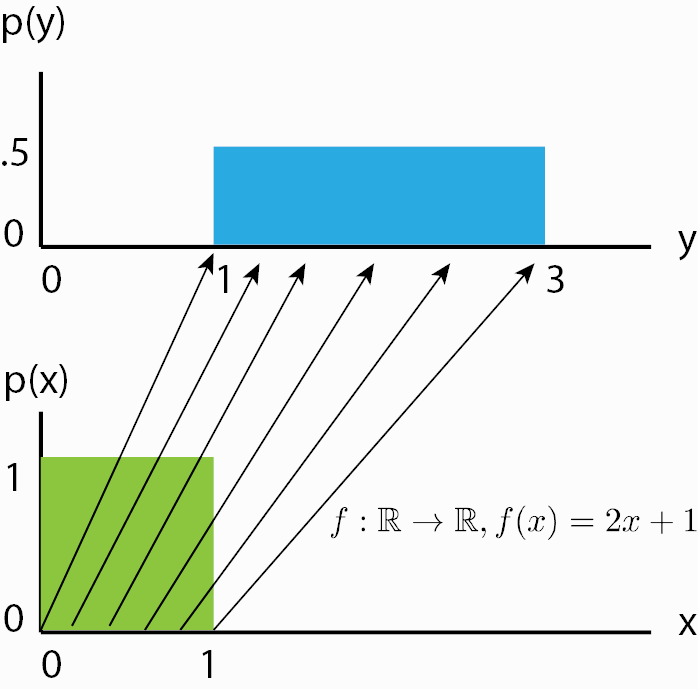
可以看到,缩放后 p ( y ) p(y) p(y)的高度应该低于 p ( x ) p(x) p(x)。这种 “体积” 变化在我们上述方程中表现为 ∣ d f ( x ) d x ∣ \left|\frac{df(x)}{dx}\right| dxdf(x) ,它确保了即使经过缩放,我们得到的仍然是一个有效的概率分布。我们可以进一步让函数 f f f变得更复杂。然而,越复杂,找到其逆函数 f − 1 f^{-1} f−1以及计算雅可比矩阵 log ∣ det d f ( x ) d x ∣ \log{} \left|\det \frac{df(\mathbf{x})}{d\mathbf{x}}\right| log detdxdf(x) 的对数行列式就越困难。一个更简便的方法是将多个可逆函数 f 1 , . . . , K f_{1,...,K} f1,...,K依次堆叠,因为总体而言,它们仍然代表一个单一的可逆函数。通过使用多个可学习的可逆函数,归一化流试图将逐步变换 p z ( z ) p_z(z) pz(z)为一个更复杂的分布,最终该分布应为 p x ( x ) p_x(x) px(x)。我们在下面对这个概念进行可视化展示:
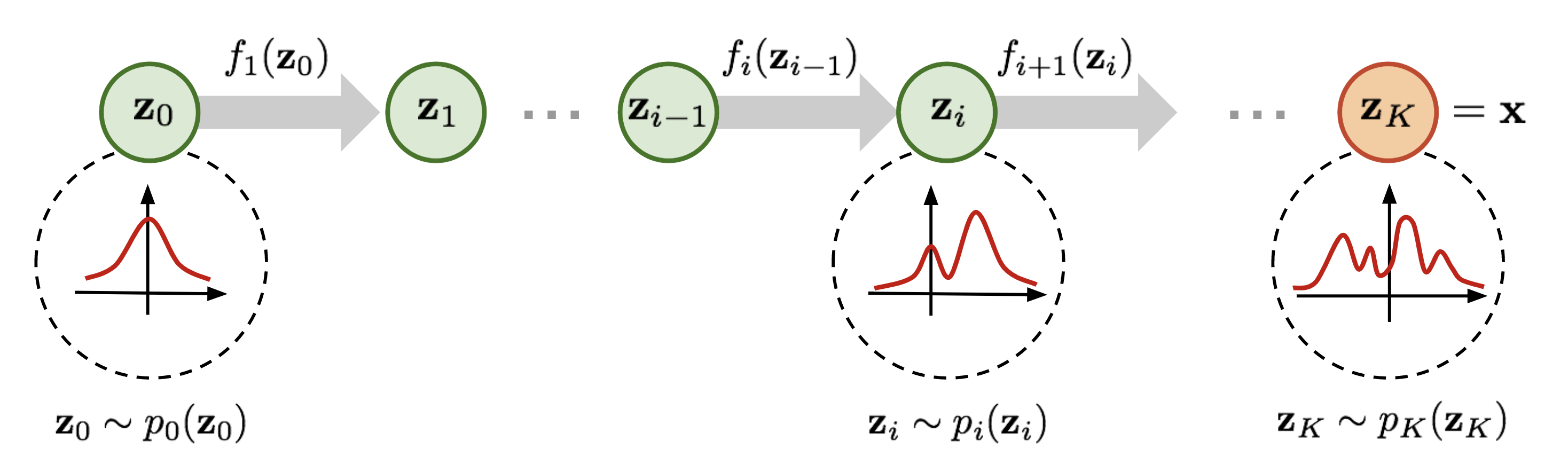
从服从先验高斯分布 z 0 z_0 z0的开始,我们依次应用可逆函数、 f 1 , f 2 , . . . , f K f_1,f_2,...,f_K f1,f2,...,fK、……、,直到 z K z_K zK表示 x x x。请注意,在上面的图中,函数 f f f表示的是我们前文提到的的反函数 f f f(此处: f : Z → X f:Z\to X f:Z→X, 上面: f : X → Z f:X\to Z f:X→Z)。这只是一种不同的表示方法,对实际的流模型设计并无影响,因为无论如何所有的 f f f都必须是可逆的。当我们如上述公式那样估计数据点 x x x的对数似然时,我们运行流的方向与上图所示相反。已经有人提出了多种使用神经网络作为可学习参数的流层,比如平面流和径向流。不过,我们这里将重点关注图像建模中常用的流,并在本笔记的剩余部分结合如何训练归一化流的细节来讨论它们。
1.3 图像归一化流核心机制剖析
要熟悉归一化流,尤其是图像建模的应用,最好讨论流中的不同元素以及实现。作为一个一般的概念,我们想要构建一个标准化流,将输入图像(这里是 MNIST)映射到大小相等的潜在空间:
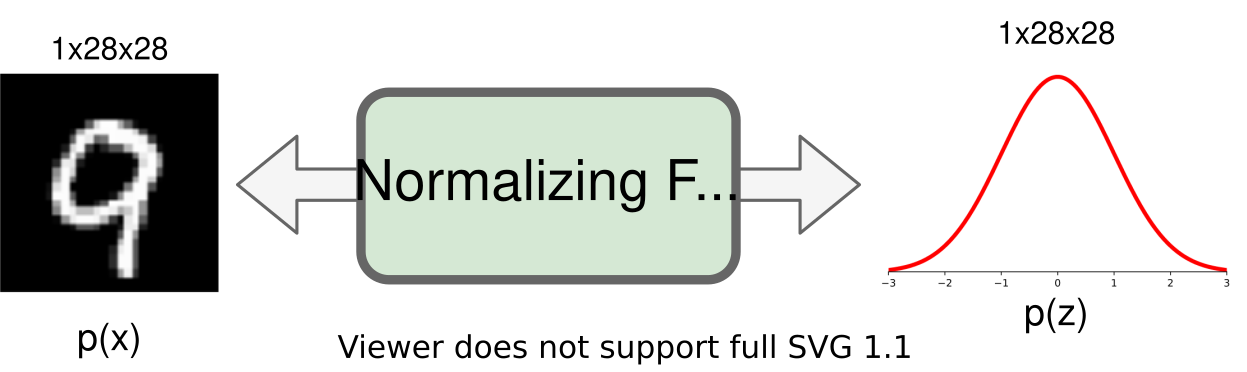
作为第一步,我们将在 PyTorch Lightning 中实现归一化流的模板。在训练和验证期间,归一化流会向前执行密度估计。为此,我们对输入 𝑥 应用一系列流变换,并通过确定给定先验的变换点 𝑧 的概率以及变换引起的体积变化来估计输入的概率。在推理过程中,我们可以通过反转流转换来进行密度估计和对新点进行采样。因此,我们定义了一个执行密度估计的函数_get_likelihood,并 sample 生成新的样本。函数 training_step 和 validation_step ``test_step 都使用 _get_likelihood 。
生成模型(尤其是标准化流)中使用的标准指标是每维度位数 (bpd)。Bpd 是从信息论的角度出发的,它描述了在建模分布中我们需要多少位来编码一个特定的示例。我们需要的 bits 越少,我们的 distribution 中的例子就越有可能。当我们测试测试数据集的每个维度的位数时,我们可以判断我们的模型是否泛化到数据集的新样本,而不是记住训练数据集。为了计算每个维度的位数分数,我们可以依赖负对数似然并更改对数基数(因为位数是二进制的,而 NLL 通常是指数的):
bpd
=
nll
⋅
log
2
(
exp
(
1
)
)
⋅
(
∏
d
i
)
−
1
\text{bpd} = \text{nll} \cdot \log_2\left(\exp(1)\right) \cdot \left(\prod d_i\right)^{-1}
bpd=nll⋅log2(exp(1))⋅(∏di)−1
其中 𝑑1,…,𝑑𝐾是 input 的维度。对于图像,这将是高度、宽度和通道号。我们将对数似然除以这些额外的维度,得到一个可以针对不同图像分辨率进行比较的指标。在原始图像空间中,MNIST 示例的每维位数分数为 8(我们需要 8 位来编码每个像素,因为有 256 个可能的值)。
class ImageFlow(pl.LightningModule):
def __init__(self, flows, import_samples=8):
"""
输入:
flows:一个由流(每个流都是一个神经网络模块(nn.Module))组成的列表,这些流应应用于图像上。
import_samples:在测试期间使用的重要性样本数量(见下面的解释)。可以在任何时候更改该数量。
"""
super().__init__()
self.flows = nn.ModuleList(flows)
self.import_samples = import_samples
# 为最终的潜在空间创建先验分布。
self.prior = torch.distributions.normal.Normal(loc=0.0, scale=1.0)
# 用于可视化图表的示例输入。
self.example_input_array = train_set[0][0].unsqueeze(dim=0)
def forward(self, imgs):
# 前向传播函数仅用于图表可视化。
return self._get_likelihood(imgs)
def encode(self, imgs):
# 给定一批图像,返回这些图像经过变换后的潜在表示 z 以及变换的对数行列式雅可比值(ldj)。
z, ldj = imgs, torch.zeros(imgs.shape[0], device=self.device)
for flow in self.flows:
z, ldj = flow(z, ldj, reverse=False)
return z, ldj
def _get_likelihood(self, imgs, return_ll=False):
"""
给定一批图像,返回这些图像的似然值。
如果 return_ll 为 True,则此函数返回输入图像的对数似然值。
否则,输出指标为每维度的比特数(经过缩放的负对数似然值)。
"""
z, ldj = self.encode(imgs)
log_pz = self.prior.log_prob(z).sum(dim=[1,2,3])
log_px = ldj + log_pz
nll = -log_px
# 计算每维度比特数
bpd = nll * np.log2(np.exp(1)) / np.prod(imgs.shape[1:])
return bpd.mean() if not return_ll else log_px
@torch.no_grad()
def sample(self, img_shape, z_init=None):
"""
Sample a batch of images from the flow.
"""
# 从先验分布中采样潜在表示。
if z_init is None:
z = self.prior.sample(sample_shape=img_shape).to(device)
else:
z = z_init.to(device)
# 通过反转流变换将潜在表示 z 转换回图像 x。
ldj = torch.zeros(img_shape[0], device=device)
for flow in reversed(self.flows):
z, ldj = flow(z, ldj, reverse=True)
return z
def configure_optimizers(self):
optimizer = optim.Adam(self.parameters(), lr=1e-3)
# 调度器是可选的,但在流模型里,它有助于实现每维度比特数(bpd)的最后一点提升。
scheduler = optim.lr_scheduler.StepLR(optimizer, 1, gamma=0.99)
return [optimizer], [scheduler]
def training_step(self, batch, batch_idx):
# 归一化流模型通过最大似然法进行训练 => 返回每维度比特数(bpd)。
loss = self._get_likelihood(batch[0])
self.log('train_bpd', loss)
return loss
def validation_step(self, batch, batch_idx):
loss = self._get_likelihood(batch[0])
self.log('val_bpd', loss)
def test_step(self, batch, batch_idx):
# 在测试阶段执行重要性采样 => 对每张图像的似然进行 M 次估计。
samples = []
for _ in range(self.import_samples):
img_ll = self._get_likelihood(batch[0], return_ll=True)
samples.append(img_ll)
img_ll = torch.stack(samples, dim=-1)
# 为了对概率进行平均,我们需要先从对数空间转换到指数空间,然后再转换回对数空间。
# 对数求和指数(LogSumExp)为我们提供了一种针对此操作的稳定实现方法。
img_ll = torch.logsumexp(img_ll, dim=-1) - np.log(self.import_samples)
# 计算最终的每维度比特数(bpd)。
bpd = -img_ll * np.log2(np.exp(1)) / np.prod(batch[0].shape[1:])
bpd = bpd.mean()
self.log('test_bpd', bpd)
该 test_step 函数与 training and validation 步骤的不同之处在于它使用重要性采样。
1.4 反量化操作
1.4.1 反量化基础流
归一化流依赖于变量变化规则,该规则在连续空间中自然定义。直接对离散数据应用流会导致不需要的密度模型,其中任意高的可能性被放置在几个特定值上。请参阅下图:
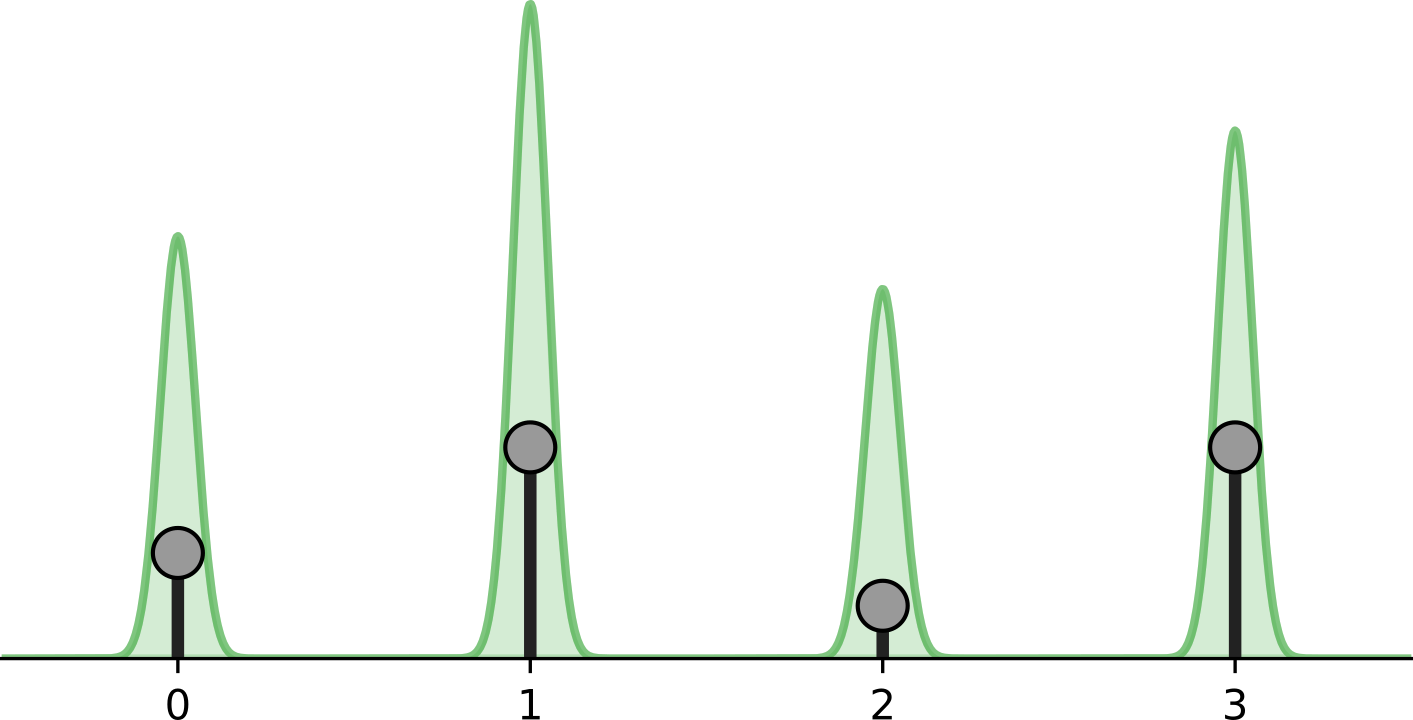
黑点表示离散点,绿色体积表示由连续空间中的归一化流建模的密度。流将继续增加可能性 , x = 0 , 1 , 2 , 3 x=0,1,2,3 x=0,1,2,3 同时在任何其他点上都没有体积。请记住,在连续空间中,我们有一个约束,即概率密度的总体积必须为 1 ( ∫ p ( x ) d x = 1 \int p(x)dx=1 ∫p(x)dx=1)。否则,我们不再对概率分布进行建模。但是,离散点 x = 0 , 1 , 2 , 3 x=0,1,2,3 x=0,1,2,3 。
表示在连续空间中没有宽度的 delta 峰值。这就是为什么流动可以在这几个点上施加无限高似然,同时仍然表示连续空间中的分布。尽管如此,学习的密度并不能告诉我们任何关于离散点之间分布的信息,因为在离散空间中,这四个点的可能性必须之和为 1,而不是无穷大。
为了防止这种退化解,一种常见的解是向每个离散值添加少量噪声,这也称为去量化。视为 𝑥 整数(就像图像一样),去量化表示 𝑣 可以表示为
v
=
x
+
u
v=x+u
v=x+u ,其中
u
∈
[
0
,
1
)
D
u\in[0,1)^D
u∈[0,1)D。因此,离散值 1 由区间
[
1.0
,
2.0
)
[1.0, 2.0)
[1.0,2.0) 上的一个分布来建模,值 2 由区间
[
2.0
,
3.0
)
[2.0, 3.0)
[2.0,3.0) 上的一个分布来建模,依此类推。我们的建模 𝑝(𝑥) 目标变为:
p
(
x
)
=
∫
p
(
x
+
u
)
d
u
=
∫
q
(
u
∣
x
)
q
(
u
∣
x
)
p
(
x
+
u
)
d
u
=
E
u
∼
q
(
u
∣
x
)
[
p
(
x
+
u
)
q
(
u
∣
x
)
]
p(x) = \int p(x+u)du = \int \frac{q(u|x)}{q(u|x)}p(x+u)du = \mathbb{E}_{u\sim q(u|x)}\left[\frac{p(x+u)}{q(u|x)} \right]
p(x)=∫p(x+u)du=∫q(u∣x)q(u∣x)p(x+u)du=Eu∼q(u∣x)[q(u∣x)p(x+u)]
其中
q
(
u
∣
x
)
q(u|x)
q(u∣x) 是噪声分布。
后面我们将把 Dequantization 实现为流变换本身。将噪声添加到离散值后,我们还将体积转换为类似高斯的形状。这是通过在 0 和 1 之间缩放 x + u x+u x+u 并应用sigmoid 函数 σ ( z ) − 1 = log z − log 1 − z \sigma(z)^{-1} = \log z - \log 1-z σ(z)−1=logz−log1−z 的反转来完成的。如果我们不这样做,我们将面临两个问题:
- 输入在 0 0 0 到 256 256 256 之间缩放,而先验分布是具有平均值 0 0 0 和标准差 1 1 1 的高斯分布。在初始化流的参数后的第一次迭代中,对于像 256 256 256 这样的大值,我们的可能性极低。这将导致训练立即发散。
- 由于输出分布是高斯分布,因此流具有类似形状的输入分布是有益的。这将降低流程所需的建模复杂性。
总的来说,我们可以按如下方式实现反量化:
class Dequantization(nn.Module):
def __init__(self, alpha=1e-5, quants=256):
"""
输入:
alpha:一个小的常量,用于对原始输入进行缩放。在对 sigmoid 函数进行求逆运算时,它可以避免处理非常接近 0 和 1 的值。
quants:可能的离散值的数量(对于 8 位图像,通常为 256) 。
"""
super().__init__()
self.alpha = alpha
self.quants = quants
def forward(self, z, ldj, reverse=False):
if not reverse:
z, ldj = self.dequant(z, ldj)
z, ldj = self.sigmoid(z, ldj, reverse=True)
else:
z, ldj = self.sigmoid(z, ldj, reverse=False)
z = z * self.quants
ldj += np.log(self.quants) * np.prod(z.shape[1:])
z = torch.floor(z).clamp(min=0, max=self.quants-1).to(torch.int32)
return z, ldj
def sigmoid(self, z, ldj, reverse=False):
if not reverse:
ldj += (-z-2*F.softplus(-z)).sum(dim=[1,2,3])
z = torch.sigmoid(z)
ldj -= np.log(1 - self.alpha) * np.prod(z.shape[1:])
z = (z - 0.5 * self.alpha) / (1 - self.alpha)
else:
z = z * (1 - self.alpha) + 0.5 * self.alpha
ldj += np.log(1 - self.alpha) * np.prod(z.shape[1:])
ldj += (-torch.log(z) - torch.log(1-z)).sum(dim=[1,2,3])
z = torch.log(z) - torch.log(1-z)
return z, ldj
def dequant(self, z, ldj):
z = z.to(torch.float32)
z = z + torch.rand_like(z).detach()
z = z / self.quants
ldj -= np.log(self.quants) * np.prod(z.shape[1:])
return z, ldj
检查流是否正确实现的一个很好的方法是验证它是否可逆。因此,我们将对随机选择的训练图像进行反量化,然后再次对其进行量化。我们预计我们会得到完全相同的图像:
pl.seed_everything(42)
orig_img = train_set[0][0].unsqueeze(dim=0)
ldj = torch.zeros(1,)
dequant_module = Dequantization()
deq_img, ldj = dequant_module(orig_img, ldj, reverse=False)
reconst_img, ldj = dequant_module(deq_img, ldj, reverse=True)
d1, d2 = torch.where(orig_img.squeeze() != reconst_img.squeeze())
if len(d1) != 0:
print("Dequantization was not invertible.")
for i in range(d1.shape[0]):
print("Original value:", orig_img[0,0,d1[i], d2[i]].item())
print("Reconstructed value:", reconst_img[0,0,d1[i], d2[i]].item())
else:
print("Successfully inverted dequantization")
生成图像和预期相同,但是,由于 S 形倒置中的数值不准确,测试可能会失败。虽然倒 sigmoid 的输入空间在 0 和 1 之间缩放,但输出空间介于 − ∞ -\infty −∞ 和 ∞ \infty ∞ 之间。由于我们使用 32 位来表示数字(除了一遍又一遍地应用日志),因此可能会发生这种不准确的情况。我们可以通过使用双张量 (float64) 进行改进。
最后,我们可以进行反量化,并实际可视化它将离散值转换为的分布:
def visualize_dequantization(quants, prior=None):
"""
用于可视化离散值在连续空间中反量化值的函数
"""
# 离散值的先验分布。若未给出,则假定为均匀分布。
if prior is None:
prior = np.ones(quants, dtype=np.float32) / quants
prior = prior / prior.sum() # 确保合适的分类分布。
inp = torch.arange(-4, 4, 0.01).view(-1, 1, 1, 1) # 我们需要考虑的可能的连续值。
ldj = torch.zeros(inp.shape[0])
dequant_module = Dequantization(quants=quants)
# 对连续值进行反量化的逆操作,以找出对应的离散值。
out, ldj = dequant_module.forward(inp, ldj, reverse=True)
inp, out, prob = inp.squeeze().numpy(), out.squeeze().numpy(), ldj.exp().numpy()
prob = prob * prior[out] # 通过分类先验进行缩放后的概率
# 绘制区间和连续分布。
sns.set_style("white")
fig = plt.figure(figsize=(6,3))
x_ticks = []
for v in np.unique(out):
indices = np.where(out==v)
color = to_rgb(f"C{v}")
plt.fill_between(inp[indices], prob[indices], np.zeros(indices[0].shape[0]), color=color+(0.5,), label=str(v))
plt.plot([inp[indices[0][0]]]*2, [0, prob[indices[0][0]]], color=color)
plt.plot([inp[indices[0][-1]]]*2, [0, prob[indices[0][-1]]], color=color)
x_ticks.append(inp[indices[0][0]])
x_ticks.append(inp.max())
plt.xticks(x_ticks, [f"{x:.1f}" for x in x_ticks])
plt.plot(inp,prob, color=(0.0,0.0,0.0))
# 设置最终绘图属性。
plt.ylim(0, prob.max()*1.1)
plt.xlim(inp.min(), inp.max())
plt.xlabel("z")
plt.ylabel("Probability")
plt.title(f"Dequantization distribution for {quants} discrete values")
plt.legend()
plt.show()
plt.close()
visualize_dequantization(quants=8)
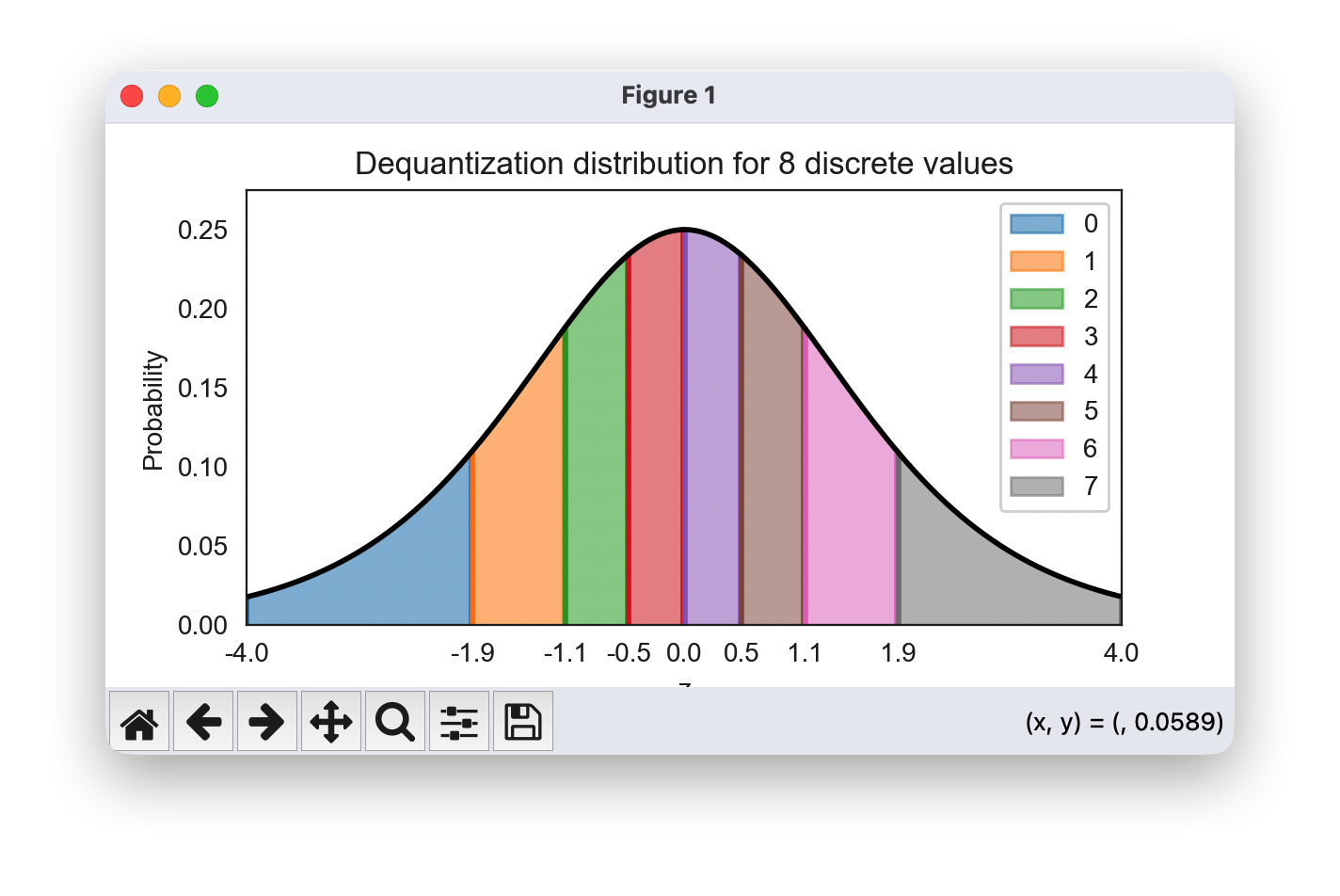
可视化分布显示分配给不同离散值的子卷。该值
0
0
0 对应的 取值区间为
[
−
∞
,
−
1.9
)
[-\infty, -1.9)
[−∞,−1.9) ,值
1
1
1 对应的区间为
[
−
1.9
,
−
1.1
)
[-1.9, -1.1)
[−1.9,−1.1) ,等等。每个离散值对应的区间具有相同的概率质量。这就是为什么靠近中心的值在z轴上对应的区间面积比其他值小(这里
z
z
z 用于表示整个反量化流的输出)。
实际上,连续归一化流通过以下目标对离散图像进行建模:
log p ( x ) = log E u ∼ q ( u ∣ x ) [ p ( x + u ) q ( u ∣ x ) ] ≥ E u [ log p ( x + u ) q ( u ∣ x ) ] \log p(x) = \log \mathbb{E}_{u\sim q(u|x)}\left[\frac{p(x+u)}{q(u|x)} \right] \geq \mathbb{E}_{u}\left[\log \frac{p(x+u)}{q(u|x)} \right] logp(x)=logEu∼q(u∣x)[q(u∣x)p(x+u)]≥Eu[logq(u∣x)p(x+u)]
尽管标准化流的可能性是精确的,但我们有一个下限。具体来说,这是 Jensen 不等式的一个例子,因为我们需要将对数移动到期望中,以便我们可以使用 Monte-carlo 估计。一般来说,这个边界比变分自动编码器中的 ELBO 小得多。实际上,我们可以通过不用 1 而是用 𝑀
样本来估计期望值来减少界限。换句话说,我们可以应用重要性抽样,这会导致以下不等式:
log p ( x ) = log E u ∼ q ( u ∣ x ) [ p ( x + u ) q ( u ∣ x ) ] ≥ E u [ log 1 M ∑ m = 1 M p ( x + u m ) q ( u m ∣ x ) ] ≥ E u [ log p ( x + u ) q ( u ∣ x ) ] \log p(x) = \log \mathbb{E}_{u\sim q(u|x)}\left[\frac{p(x+u)}{q(u|x)} \right] \geq \mathbb{E}_{u}\left[\log \frac{1}{M} \sum_{m=1}^{M} \frac{p(x+u_m)}{q(u_m|x)} \right] \geq \mathbb{E}_{u}\left[\log \frac{p(x+u)}{q(u|x)} \right] logp(x)=logEu∼q(u∣x)[q(u∣x)p(x+u)]≥Eu[logM1m=1∑Mq(um∣x)p(x+um)]≥Eu[logq(u∣x)p(x+u)]
重要性抽样
1
M
∑
m
=
1
M
p
(
x
+
u
m
)
q
(
u
m
∣
x
)
\frac{1}{M} \sum_{m=1}^{M} \frac{p(x+u_m)}{q(u_m|x)}
M1∑m=1Mq(um∣x)p(x+um) 变为
E
u
∼
q
(
u
∣
x
)
[
p
(
x
+
u
)
q
(
u
∣
x
)
]
\mathbb{E}_{u\sim q(u|x)}\left[\frac{p(x+u)}{q(u|x)} \right]
Eu∼q(u∣x)[q(u∣x)p(x+u)] 如果
M
→
∞
M\to \infty
M→∞,因此我们使用的样本越多,界限就越紧密。在测试期间,我们可以利用此属性并在test_step中ImageFlow实现它。理论上,我们也可以在训练期间使用这个 tighter bound。然而,相关研究表明,考虑到额外的计算成本,这不一定会导致改进,并且坚持单一估计更有效。
1.4.2 变分反量化
反量化对噪声 u u u 使用均匀分布,这有效地导致图像被表示为具有清晰边界的超立方体(高维立方体)。然而,对如此清晰的边界进行建模对于流动来说并不容易,因为它使用平滑变换将其转换为高斯分布。
另一种看待它的方法是,如果我们更改了前一个可视化中的先验分布。想象一下,我们在像素上有独立的高斯噪声,这在任何真实世界拍摄的照片中都是常见的。因此,流必须按上述方式对分布进行建模,但各个体积的缩放方式如下:
visualize_dequantization(quants=8, prior=np.array([0.075, 0.2, 0.4, 0.2, 0.075, 0.025, 0.0125, 0.0125]))
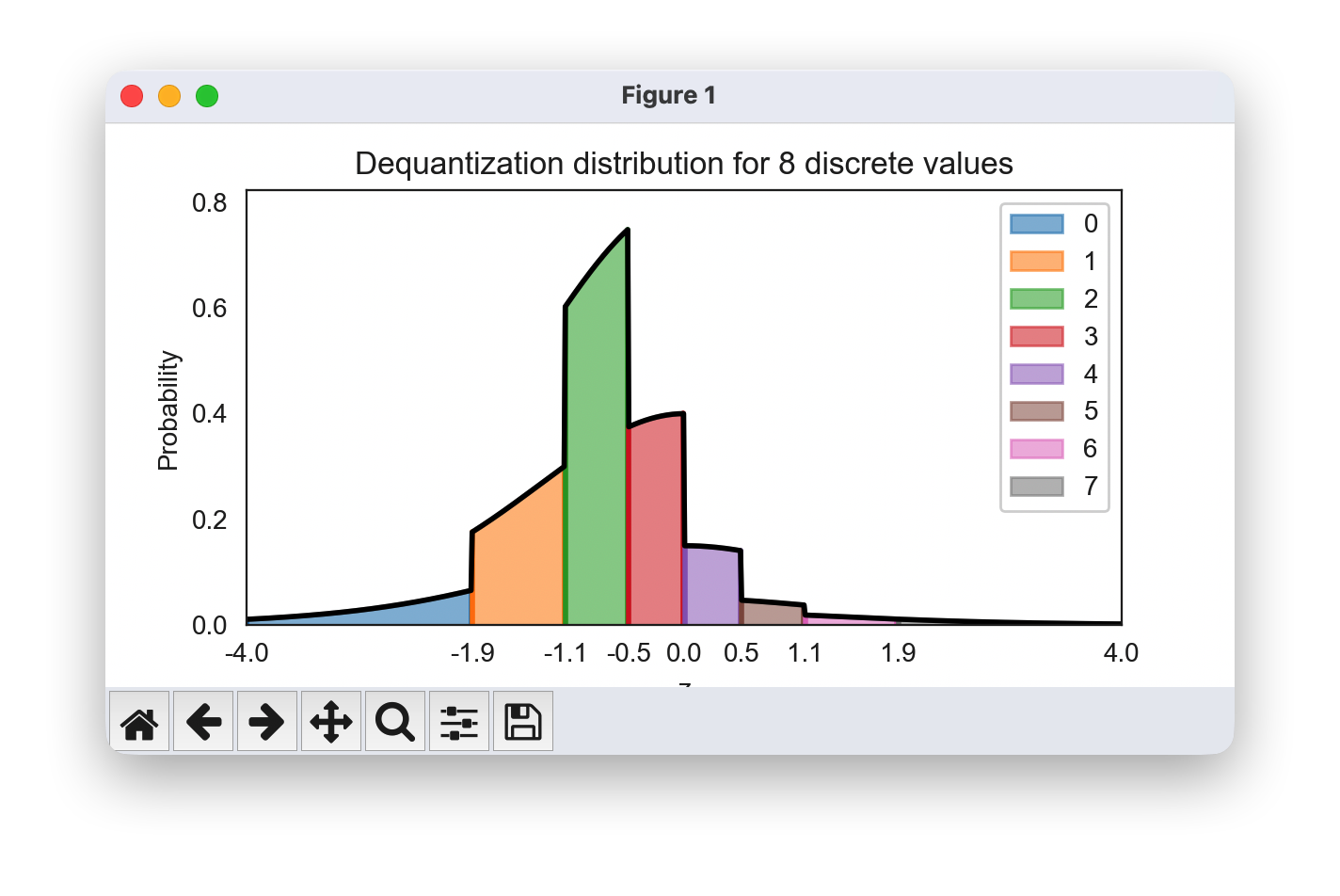
将这样的概率转化为高斯分布是一项艰巨的任务,尤其是在如此硬的边界下。因此,反量化已扩展到变分框架中超越 uniform 的更复杂、可学习的分布。特别是,如果我们记住 learning objective log p ( x ) = log E u [ p ( x + u ) q ( u ∣ x ) ] \log p(x) = \log \mathbb{E}_{u}\left[\frac{p(x+u)}{q(u|x)} \right] logp(x)=logEu[q(u∣x)p(x+u)],均匀分布可以被一个通过学习得到的分布 q θ ( u ∣ x ) q_{\theta}(u|x) qθ(u∣x) 所替代,该分布的取值范围为 u ∈ [ 0 , 1 ) D u\in[0,1)^D u∈[0,1)D,这种方法被称为变分反量化。我们如何学习这样的分布?我们可以使用第二个归一化流,它将 x x x 作为外部输入,并学习关于 u u u 的一个灵活分布。为了确保取值范围在 [ 0 , 1 ) D [0,1)^D [0,1)D 内,我们可以应用一个 sigmoid 激活函数作为最终的流变换。
继承了原来的 dequantization 类,我们可以按如下方式实现变分去量化:
class VariationalDequantization(Dequantization):
def __init__(self, var_flows, alpha=1e-5):
"""
输入:
var_flows:用于对 q(u|x) 进行建模的一系列流变换。
alpha:小常数,具体细节见反量化部分。
"""
super().__init__(alpha=alpha)
self.flows = nn.ModuleList(var_flows)
def dequant(self, z, ldj):
z = z.to(torch.float32)
img = (z / 255.0) * 2 - 1 # 我们以 x(即原始图像)为条件来进行流变换。
# 和之前一样,u 的先验分布是均匀分布。
# 由于大多数流变换是在 [-infinity,+infinity] 上定义的,所以我们首先应用反 Sigmoid 函数。
deq_noise = torch.rand_like(z).detach()
deq_noise, ldj = self.sigmoid(deq_noise, ldj, reverse=True)
for flow in self.flows:
deq_noise, ldj = flow(deq_noise, ldj, reverse=False, orig_img=img)
deq_noise, ldj = self.sigmoid(deq_noise, ldj, reverse=False)
# 在完成流变换之后,像标准反量化那样应用 u。
z = (z + deq_noise) / 256.0
ldj -= np.log(256.0) * np.prod(z.shape[1:])
return z, ldj
变分反量化可以替代反量化。我们将在以后的实验中比较去量化和变分去量化。
1.5 模型构建与训练
1.5.1 耦合层在模型中的构建
接下来,我们探讨在流中可以应用的可能变换,如耦合层:输入 z z z 被任意拆分为两部分,即 z 1 : j z_{1:j} z1:j 和 z j + 1 : d z_{j+1:d} zj+1:d,其中第一部分在流变换中保持不变。不过, z 1 : j z_{1:j} z1:j 被用于为第二部分 z j + 1 : d z_{j+1:d} zj+1:d 的变换提供参数。近期已经提出了多种变换方法,但在这里我们将采用最简单且最有效的一种:仿射耦合。在这个耦合层中,我们通过一个偏置项 μ \mu μ 对输入进行偏移,并通过缩放因子 σ \sigma σ 对其进行缩放,以此来应用仿射变换。换句话说,我们的变换形式如下:
z j + 1 : d ′ = μ θ ( z 1 : j ) + σ θ ( z 1 : j ) ⊙ z j + 1 : d z'_{j+1:d} = \mu_{\theta}(z_{1:j}) + \sigma_{\theta}(z_{1:j}) \odot z_{j+1:d} zj+1:d′=μθ(z1:j)+σθ(z1:j)⊙zj+1:d
函数 μ \mu μ 和 σ \sigma σ 作为共享神经网络实现,求和和乘法按元素执行。因此,LDJ 是比例因子的对数之和: ∑ i [ log σ θ ( z 1 : j ) ] i \sum_i \left[\log \sigma_{\theta}(z_{1:j})\right]_i ∑i[logσθ(z1:j)]i。反转层可以简单地完成,只需减去偏差并除以比例即可:
z j + 1 : d = ( z j + 1 : d ′ − μ θ ( z 1 : j ) ) / σ θ ( z 1 : j ) z_{j+1:d} = \left(z'_{j+1:d} - \mu_{\theta}(z_{1:j})\right) / \sigma_{\theta}(z_{1:j}) zj+1:d=(zj+1:d′−μθ(z1:j))/σθ(z1:j)
我们还可以将耦合层以计算图的形式可视化,其中 z 1 z_1 z1 表示 z 1 : j z_{1:j} z1:j , z 2 z_2 z2 表示 z j + 1 : d z_{j+1:d} zj+1:d :
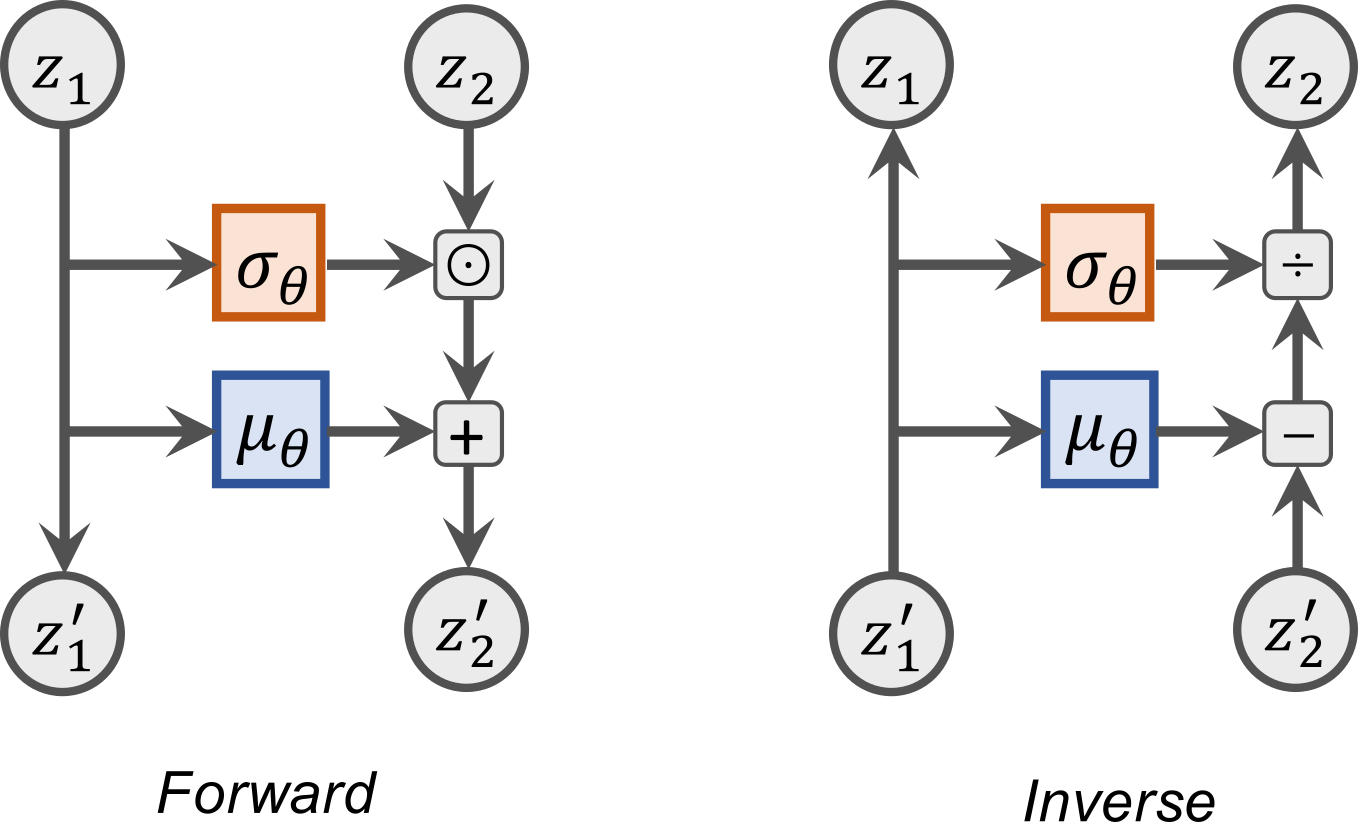
在我们的实现中,我们将把变量的拆分操作实现为掩码操作。当把 z z z 输入到共享网络以预测变换参数时,待变换的变量 z j + 1 : d z_{j+1:d} zj+1:d 会被掩码处理。在应用变换时,我们会对 z 1 : j z_{1:j} z1:j 对应的参数进行掩码处理,这样对于这些变量就相当于进行了恒等变换:
class CouplingLayer(nn.Module):
def __init__(self, network, mask, c_in):
super().__init__()
self.network = network
self.scaling_factor = nn.Parameter(torch.zeros(c_in))
# 将掩码注册为缓冲区,因为它是一个张量,虽不是参数,但应作为模块状态的一部分。
self.register_buffer('mask', mask)
def forward(self, z, ldj, reverse=False, orig_img=None):
# 对经过掩码处理的输入应用网络
z_in = z * self.mask
if orig_img is None:
nn_out = self.network(z_in)
else:
nn_out = self.network(torch.cat([z_in, orig_img], dim=1))
s, t = nn_out.chunk(2, dim=1)
# 稳定缩放输出
s_fac = self.scaling_factor.exp().view(1, -1, 1, 1)
s = torch.tanh(s / s_fac) * s_fac
# 对输出进行掩码处理(仅变换第二部分)
s = s * (1 - self.mask)
t = t * (1 - self.mask)
# 仿射变换
if not reverse:
# 我们是先进行偏移再进行缩放,还是反之,这是一个设计选择,通常不会产生太大影响
z = (z + t) * torch.exp(s)
ldj += s.sum(dim=[1,2,3])
else:
z = (z * torch.exp(-s)) - t
ldj -= s.sum(dim=[1,2,3])
return z, ldj
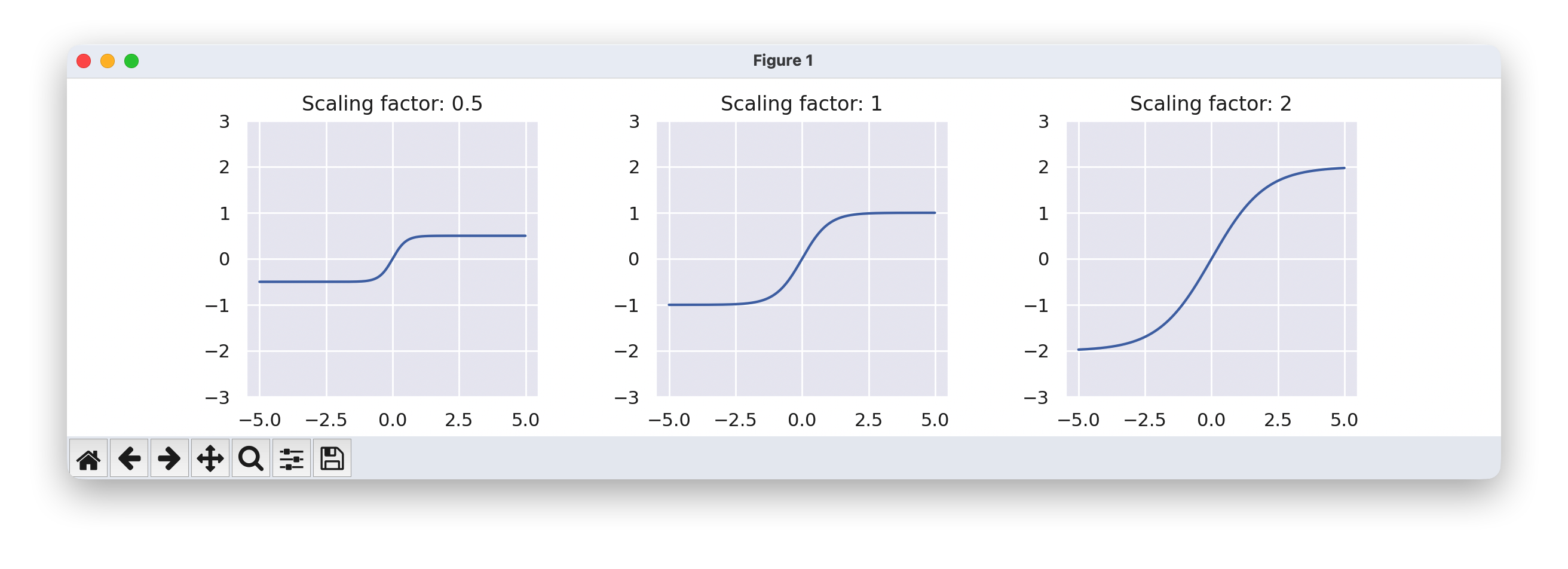
为了达到稳定目的,我们在缩放输出上应用了
tanh
\tanh
tanh 激活函数。这可以防止缩放的突然大输出值,这可能会破坏训练的稳定性。为了仍然允许分别小于或大于 -1 和 1 的缩放因子,我们为每个维度提供了一个可学习的参数,称为scaling_factor。这会将
tanh
\tanh
tanh 缩放到不同的限制。下面,我们可视化了比例因子对缩放项输出激活的影响:
with torch.no_grad():
x = torch.arange(-5,5,0.01)
scaling_factors = [0.5, 1, 2]
sns.set()
fig, ax = plt.subplots(1, 3, figsize=(12,3))
for i, scale in enumerate(scaling_factors):
y = torch.tanh(x / scale) * scale
ax[i].plot(x.numpy(), y.numpy())
ax[i].set_title("Scaling factor: " + str(scale))
ax[i].set_ylim(-3, 3)
plt.subplots_adjust(wspace=0.4)
sns.reset_orig()
plt.show()
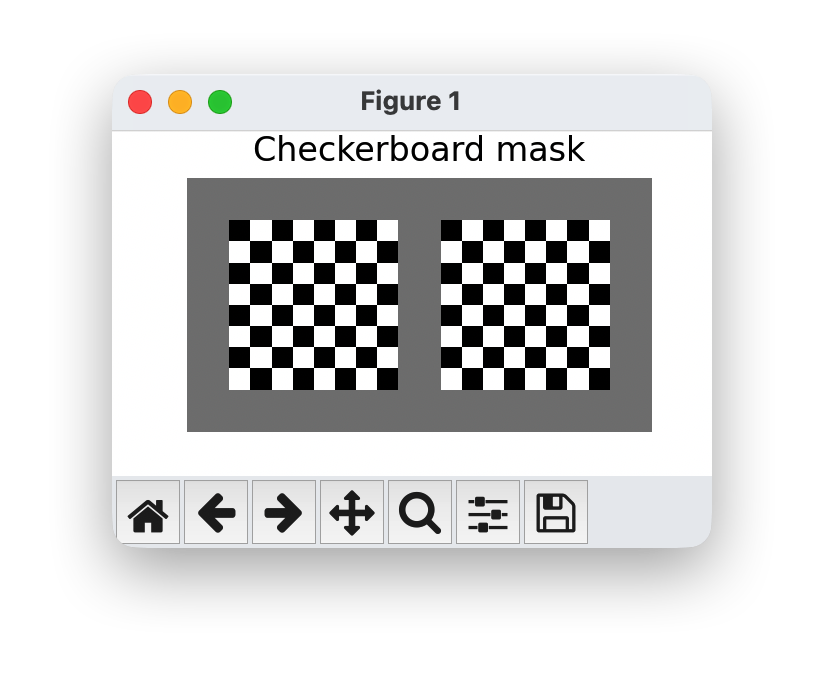
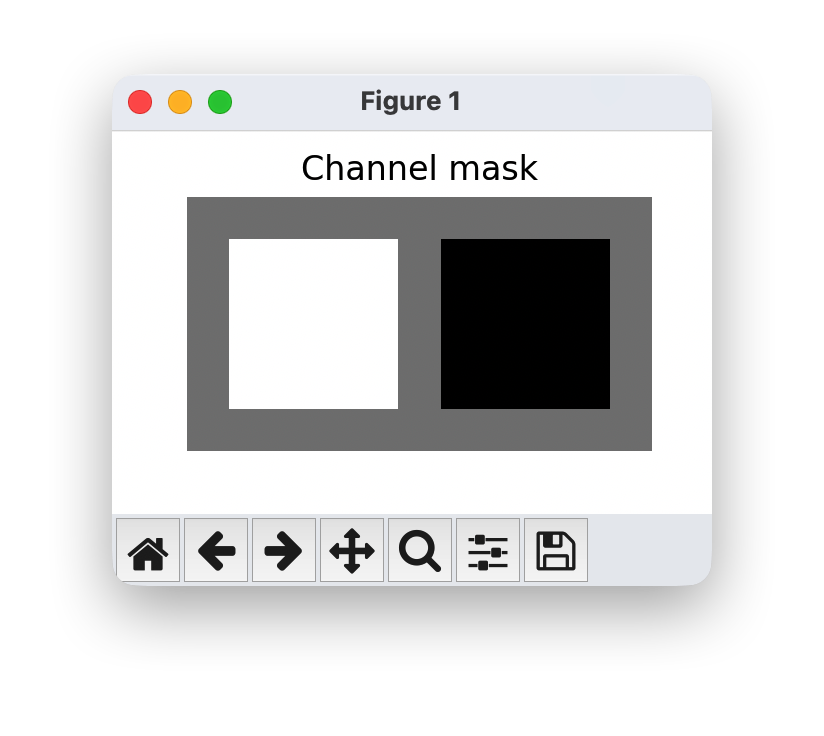
耦合层可以推广到我们能想到的任何掩码技术。但是,图像最常见的方法是使用棋盘遮罩或通道遮罩将输入 z z z 一分为二。棋盘遮罩在高度和宽度维度上拆分变量,并将每个像素分配给 z j + 1 : d z_{j+1:d} zj+1:d。因此,掩码在通道之间共享。相反,通道掩码将一半的通道 分配给 z j + 1 : d z_{j+1:d} zj+1:d ,另一半分配给 z 1 : j + 1 z_{1:j+1} z1:j+1 。请注意,当我们应用多个耦合层时,我们会反转每个其他层的掩码,以便每个变量变换相似的次数。
让我们实现一个函数,为我们创建一个棋盘面罩和一个通道掩码:
def create_checkerboard_mask(h, w, invert=False):
x, y = torch.arange(h, dtype=torch.int32), torch.arange(w, dtype=torch.int32)
xx, yy = torch.meshgrid(x, y, indexing='ij')
mask = torch.fmod(xx + yy, 2)
mask = mask.to(torch.float32).view(1, 1, h, w)
if invert:
mask = 1 - mask
return mask
def create_channel_mask(c_in, invert=False):
mask = torch.cat([torch.ones(c_in//2, dtype=torch.float32),
torch.zeros(c_in-c_in//2, dtype=torch.float32)])
mask = mask.view(1, c_in, 1, 1)
if invert:
mask = 1 - mask
return mask
我们还可以可视化一个大小为 8×8×2(2 个通道)的图像对应的掩码(masks):
checkerboard_mask = create_checkerboard_mask(h=8, w=8).expand(-1,2,-1,-1)
channel_mask = create_channel_mask(c_in=2).expand(-1,-1,8,8)
show_imgs(checkerboard_mask.transpose(0,1), "Checkerboard mask")
show_imgs(channel_mask.transpose(0,1), "Channel mask")
作为耦合层的最后一个方面,我们需要确定要在耦合层中应用的深度神经网络。层的输入是图像,因此我们坚持使用 CNN。由于转换的输入取决于之前的所有转换,因此确保通过 CNN 的良好梯度流回输入至关重要,这可以通过类似 ResNet 的架构最佳实现。具体来说,我们使用一个门控 ResNet,它向 skip 连接添加一个 σ \sigma σ-gate,类似于 LSTM 中的输入门。
class ConcatELU(nn.Module):
"""
一种在正向和反向(即正常和反转方向)都应用指数线性单元(ELU)的激活函数。它在提供非线性特性的同时,能为任意输入提供强梯度(这对最终的卷积操作很重要)。
"""
def forward(self, x):
return torch.cat([F.elu(x), F.elu(-x)], dim=1)
class LayerNormChannels(nn.Module):
def __init__(self, c_in, eps=1e-5):
"""
该模块对图像各通道应用层归一化(Layer Normalization)。
输入:
c_in:输入的通道数
eps:用于稳定标准差的小常数
"""
super().__init__()
self.gamma = nn.Parameter(torch.ones(1, c_in, 1, 1))
self.beta = nn.Parameter(torch.zeros(1, c_in, 1, 1))
self.eps = eps
def forward(self, x):
mean = x.mean(dim=1, keepdim=True)
var = x.var(dim=1, unbiased=False, keepdim=True)
y = (x - mean) / torch.sqrt(var + self.eps)
y = y * self.gamma + self.beta
return y
class GatedConv(nn.Module):
def __init__(self, c_in, c_hidden):
"""
该模块应用一个带有输入门控的两层卷积残差网络(ResNet)块。
输入:
c_in:输入的通道数
c_hidden:我们想要建模的隐藏维度数量(通常与 c_in 相近)
"""
super().__init__()
self.net = nn.Sequential(
ConcatELU(),
nn.Conv2d(2*c_in, c_hidden, kernel_size=3, padding=1),
ConcatELU(),
nn.Conv2d(2*c_hidden, 2*c_in, kernel_size=1)
)
def forward(self, x):
out = self.net(x)
val, gate = out.chunk(2, dim=1)
return x + val * torch.sigmoid(gate)
class GatedConvNet(nn.Module):
def __init__(self, c_in, c_hidden=32, c_out=-1, num_layers=3):
"""
此模块应用一个带输入门控的两层卷积残差网络(ResNet)模块。
输入:
c_in:输入的通道数
c_hidden:我们希望建模的隐藏层维度数量(通常与 c_in 相近)
"""
super().__init__()
c_out = c_out if c_out > 0 else 2 * c_in
layers = []
layers += [nn.Conv2d(c_in, c_hidden, kernel_size=3, padding=1)]
for layer_index in range(num_layers):
layers += [GatedConv(c_hidden, c_hidden),
LayerNormChannels(c_hidden)]
layers += [ConcatELU(),
nn.Conv2d(2*c_hidden, c_out, kernel_size=3, padding=1)]
self.nn = nn.Sequential(*layers)
self.nn[-1].weight.data.zero_()
self.nn[-1].bias.data.zero_()
def forward(self, x):
return self.nn(x)
1.5.2 训练循环的设计与实现
最后,我们可以将 Dequantization、Variational Dequantization 和 Coupling Layers 添加在一起,以在 MNIST 图像上构建完整的归一化流。我们在主流中应用 8 个耦合层,如果应用,则应用 4 个耦合层用于变分反量化。我们在整个网络中应用棋盘格掩码(checkerboard mask),因为单通道(黑白图像)无法应用通道掩码(channel mask)。整体架构如下所示。
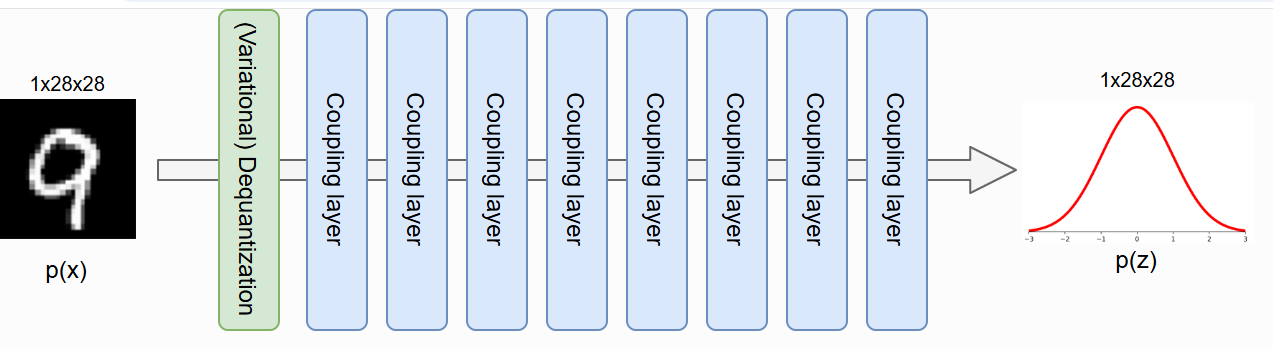
def create_simple_flow(use_vardeq=True):
flow_layers = []
if use_vardeq:
vardeq_layers = [CouplingLayer(network=GatedConvNet(c_in=2, c_out=2, c_hidden=16),
mask=create_checkerboard_mask(h=28, w=28, invert=(i%2==1)),
c_in=1) for i in range(4)]
flow_layers += [VariationalDequantization(var_flows=vardeq_layers)]
else:
flow_layers += [Dequantization()]
for i in range(8):
flow_layers += [CouplingLayer(network=GatedConvNet(c_in=1, c_hidden=32),
mask=create_checkerboard_mask(h=28, w=28, invert=(i%2==1)),
c_in=1)]
flow_model = ImageFlow(flow_layers).to(device)
return flow_model
为了实现训练循环,我们使用 PyTorch Lightning 的框架,以减少代码开销。如果有兴趣,您可以查看生成的 tensorboard 文件,特别是图表,以查看所应用的流转换的概述。请注意,我们再次提供了预训练模型,因为归一化流的训练成本特别高。我们还进行了验证和测试,因为这可能需要一些时间,并且抽样的重要性也会增加。
注意:此样例中为了快速跑完全流程进行体验,将
max_epochs设置为了50,太少得训练轮次往往不会获得太好得训练结果,您可以进行修改相关参数进行尝试,比如,您可以设置max_epochs为200,以充分训练模型。后续所有得结论都是模型得到充分训练之后进行讨论得!
def train_flow(flow, model_name="MNISTFlow"):
# 创建一个 PyTorch Lightning 训练器
trainer = pl.Trainer(default_root_dir=os.path.join(CHECKPOINT_PATH, model_name),
accelerator="npu",
devices=1,
max_epochs=50,
gradient_clip_val=1.0,
callbacks=[ModelCheckpoint(save_weights_only=True, mode="min", monitor="val_bpd"),
LearningRateMonitor("epoch")],
check_val_every_n_epoch=1)
trainer.logger._log_graph = True
trainer.logger._default_hp_metric = None # 可选的日志记录参数,我们不需要这个参数。
train_data_loader = data.DataLoader(train_set, batch_size=512, shuffle=True, drop_last=True, pin_memory=True, num_workers=8)
result = None
# 检查预训练模型是否存在。如果存在,则加载该模型并跳过训练过程。
pretrained_filename = os.path.join(CHECKPOINT_PATH, model_name + ".ckpt")
if os.path.isfile(pretrained_filename):
print("Found pretrained model, loading...")
ckpt = torch.load(pretrained_filename, map_location=device)
flow.load_state_dict(ckpt['state_dict'])
result = ckpt.get("result", None)
else:
print("Start training", model_name)
trainer.fit(flow, train_data_loader, val_loader)
# 如果尚未得到结果,则在验证集和测试集上对最优模型进行测试。由于重要性采样,测试过程可能会很耗时。
if result is None:
val_result = trainer.test(flow, val_loader, verbose=False)
start_time = time.time()
test_result = trainer.test(flow, test_loader, verbose=False)
duration = time.time() - start_time
result = {"test": test_result, "val": val_result, "time": duration / len(test_loader) / flow.import_samples}
return flow, result
1.5.3 多尺度架构
归一化流的一个缺点是它们在与输入完全相同的维度上运行。如果输入是高维的,则潜在空间也是高维的,这需要更大的计算成本来学习合适的转换。然而,特别是在图像域中,许多像素包含的信息较少,因为我们可以在不丢失图像语义信息的情况下删除它们。
基于这种直觉,图像上的深度归一化流通常应用多尺度架构。在第一次
N
N
N 流转换之后,我们拆分了一半的潜在维度,并直接在前一个维度上评估它们。另一半通过
N
N
N 更多的流转换运行,根据输入的大小,我们再次将其分成两半或在此位置整体停止。此设置中涉及的两个作是 Squeeze , Split 我们将在下面更仔细地查看和实施。
1.5.4 挤压和拆分
当我们想删除图像中的一半像素时,我们面临着决定要剪切哪些变量以及如何重新排列图像的问题。因此,通常在 split 之前使用挤压作,它将图像划分为 2 × 2 × C 2\times 2\times C 2×2×C 的子方块,并将它们重塑为 1 × 1 × 4 C 1\times 1\times 4C 1×1×4C 块。实际上,我们将图像的高度和宽度减少了 2 倍,同时将通道数缩放了 4 倍。之后,我们可以在通道维度上执行分割操作,而无需重新排列像素。较小的规模也使整体架构更加高效。从视觉上看,squeeze作应按如下方式转换输入:
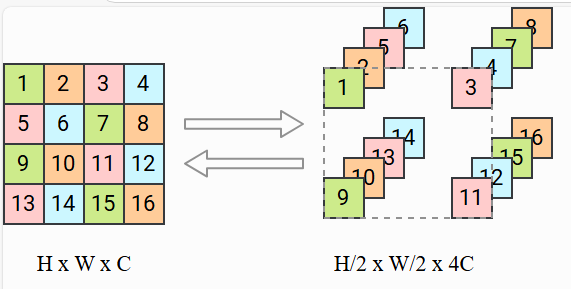
将 4 × 4 × 1 4\times 4\times 1 4×4×1 的输入按照把像素划分为 2 × 2 × 1 2\times 2\times 1 2×2×1 子方块的思路缩放为 2 × 2 × 4 2\times 2\times 4 2×2×4。接下来,让我们尝试实现这一层。
class SqueezeFlow(nn.Module):
def forward(self, z, ldj, reverse=False):
B, C, H, W = z.shape
if not reverse:
# 前向传播方向:H x W x C => H/2 x W/2 x 4C。
z = z.reshape(B, C, H//2, 2, W//2, 2)
z = z.permute(0, 1, 3, 5, 2, 4)
z = z.reshape(B, 4*C, H//2, W//2)
else:
# 反向传播方向:H/2 x W/2 x 4C => H x W x C
z = z.reshape(B, C//4, 2, 2, H, W)
z = z.permute(0, 1, 4, 2, 5, 3)
z = z.reshape(B, C//4, H*2, W*2)
return z, ldj
在继续之前,我们可以通过将我们的输出与上面的示例图进行比较来验证我们的实现:
sq_flow = SqueezeFlow()
rand_img = torch.arange(1,17).view(1, 1, 4, 4)
print("Image (before)\n", rand_img)
forward_img, _ = sq_flow(rand_img, ldj=None, reverse=False)
print("\nImage (forward)\n", forward_img.permute(0,2,3,1)) # 为了提高可读性而进行维度置换。
reconst_img, _ = sq_flow(forward_img, ldj=None, reverse=True)
print("\nImage (reverse)\n", reconst_img)
分割操作会将输入划分为两部分,并直接根据先验分布对其中一部分进行评估。为了使我们的流操作与前面各层的实现相适配,我们会将第一部分的先验概率作为该层的雅可比行列式的对数返回。这与我们在流操作结束时将所有变量分割结果合并起来,并一起根据先验分布进行评估具有相同的效果。
class SplitFlow(nn.Module):
def __init__(self):
super().__init__()
self.prior = torch.distributions.normal.Normal(loc=0.0, scale=1.0)
def forward(self, z, ldj, reverse=False):
if not reverse:
z, z_split = z.chunk(2, dim=1)
ldj += self.prior.log_prob(z_split).sum(dim=[1,2,3])
else:
z_split = self.prior.sample(sample_shape=z.shape).to(device)
z = torch.cat([z, z_split], dim=1)
ldj -= self.prior.log_prob(z_split).sum(dim=[1,2,3])
return z, ldj
1.5.5 多尺度流的构建
在定义了 squeeze 和 split作之后,我们终于能够构建自己的多尺度流。深度归一化流(如 Glow 和 Flow++)通常在压缩后直接应用拆分作。但是,对于浅流,我们需要更加仔细地考虑将 split作放置在何处,因为我们至少需要对每个变量进行最少数量的转换。我们的设置受到原始 RealNVP 架构的启发,它比其他最新的最先进的架构要浅。
因此,对于 MNIST 数据集,我们将在两个耦合层之后应用第一个 squeeze作,但暂时不应用拆分作。因为我们只使用了两个耦合层,而且每个变量只变换了一次,所以拆分作还为时过早。在最后应用分流并再次挤压之前,我们再应用两个耦合层。最后四个耦合层的尺度 为 7 × 7 × 8 7\times 7\times 8 7×7×8。全流程架构如下所示。
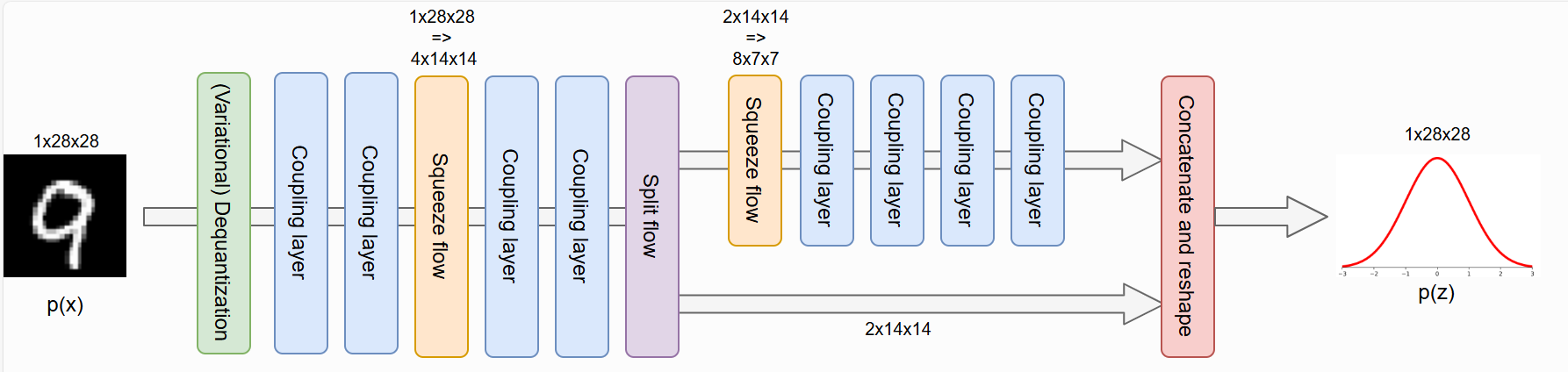
请注意,虽然耦合层内的特征图随着输入的高度和宽度而减小,但通道数的增加并没有直接考虑。为了解决这个问题,我们增加了 squeezed input 上耦合层的隐藏维度。维度通常缩放 2,因为这大约会使计算成本增加 4,而使用压缩作会取消。但是,我们将分别为三个尺度选择隐藏维度 32 , 48 , 64 32, 48, 64 32,48,64,以保持参数数量的合理性,并展示多尺度架构的效率。
def create_multiscale_flow():
flow_layers = []
vardeq_layers = [CouplingLayer(network=GatedConvNet(c_in=2, c_out=2, c_hidden=16),
mask=create_checkerboard_mask(h=28, w=28, invert=(i%2==1)),
c_in=1) for i in range(4)]
flow_layers += [VariationalDequantization(vardeq_layers)]
flow_layers += [CouplingLayer(network=GatedConvNet(c_in=1, c_hidden=32),
mask=create_checkerboard_mask(h=28, w=28, invert=(i%2==1)),
c_in=1) for i in range(2)]
flow_layers += [SqueezeFlow()]
for i in range(2):
flow_layers += [CouplingLayer(network=GatedConvNet(c_in=4, c_hidden=48),
mask=create_channel_mask(c_in=4, invert=(i%2==1)),
c_in=4)]
flow_layers += [SplitFlow(),
SqueezeFlow()]
for i in range(4):
flow_layers += [CouplingLayer(network=GatedConvNet(c_in=8, c_hidden=64),
mask=create_channel_mask(c_in=8, invert=(i%2==1)),
c_in=8)]
flow_model = ImageFlow(flow_layers).to(device)
return flow_model
我们可以在下面显示参数数量的差异:
def print_num_params(model):
num_params = sum([np.prod(p.shape) for p in model.parameters()])
print("Number of parameters: {:,}".format(num_params))
print_num_params(create_simple_flow(use_vardeq=False))
print_num_params(create_simple_flow(use_vardeq=True))
print_num_params(create_multiscale_flow())
尽管多尺度流的参数几乎是单尺度流的 3 倍,但它的计算成本不一定比同类流高。我们还将在以下实验中比较运行时间。
1.6 训练流变体
1.6.1 分析流特性及应用
在实验的最后一部分,我们将训练上面实现的所有模型,并尝试分析多尺度架构和变分反量化的效果。
在分析流模型之前,我们需要先训练它们。下面提供预训练模型,其中包含验证和测试性能以及运行时信息。
flow_dict = {"simple": {}, "vardeq": {}, "multiscale": {}}
flow_dict["simple"]["model"], flow_dict["simple"]["result"] = train_flow(create_simple_flow(use_vardeq=False), model_name="MNISTFlow_simple")
flow_dict["vardeq"]["model"], flow_dict["vardeq"]["result"] = train_flow(create_simple_flow(use_vardeq=True), model_name="MNISTFlow_vardeq")
flow_dict["multiscale"]["model"], flow_dict["multiscale"]["result"] = train_flow(create_multiscale_flow(), model_name="MNISTFlow_multiscale")
flow_dict["simple"]["result"]
Out:
{‘test’: [{‘test_bpd’: 1.816909670829773}],
‘val’: [{‘test_bpd’: 1.8728876113891602}],
‘time’: 0.038458727300167084}
1.6.2 密度建模和采样
首先,我们可以根据模型的定量结果进行比较。下表显示了所有重要的统计信息。推理时间指定确定每个模型出现一批 64 张图像的概率所需的时间,采样时间表示对一批 64 张图像进行采样所花费的持续时间。
%%html
<!-- Some HTML code to increase font size in the following table -->
<style>
th {font-size: 120%;}
td {font-size: 120%;}
</style>
import tabulate
from IPython.display import display, HTML
table = [[key,
"%4.3f bpd" % flow_dict[key]["result"]["val"][0]["test_bpd"],
"%4.3f bpd" % flow_dict[key]["result"]["test"][0]["test_bpd"],
"%2.0f ms" % (1000 * flow_dict[key]["result"]["time"]),
"%2.0f ms" % (1000 * flow_dict[key]["result"].get("samp_time", 0)),
"{:,}".format(sum([np.prod(p.shape) for p in flow_dict[key]["model"].parameters()]))]
for key in flow_dict]
display(HTML(tabulate.tabulate(table, tablefmt='html', headers=["Model", "Validation Bpd", "Test Bpd", "Inference time", "Sampling time", "Num Parameters"])))

由于只训练了50个批次,所以对比效果可能不是很明显,你可以多训练几个批次对比一下。
接下来测试模型的采样质量。注意到变分反量化和标准反量化的样本非常相似,因此我们在这里只可视化变分反量化和多尺度模型的样本。但是,您也可以随意测试该 "simple" 模型。
pl.seed_everything(44)
samples = flow_dict["vardeq"]["model"].to(device).sample(img_shape=[16,1,28,28])
show_imgs(samples.cpu())

pl.seed_everything(42)
samples = flow_dict["multiscale"]["model"].to(device).sample(img_shape=[16,8,7,7])
show_imgs(samples.cpu())

从以上我们可以看到简单模型和多尺度模型之间的明显差异。单尺度模型只学习了局部的、小的相关性,而多尺度模型能够学习形成数字的完整、全局的关系。这展示了多尺度模型的另一个好处。与 VAE 相比,VAE 的输出非常清晰,因为归一化流可以自然地模拟复杂的多模态分布,而 VAE 具有独立的解码器输出噪声。然而,该流程中的样本远非完美,因为并非所有样本都显示真实数字。
1.6.3 潜在空间中的插值
生成模型潜在空间平滑度的另一个流行测试是在两个训练示例之间进行插值。由于归一化流是严格可逆的,因此我们可以保证任何图像都在潜在空间中表示。我们再次将变分反量化模型与下面的多尺度模型进行了比较。
@torch.no_grad()
def interpolate(model, img1, img2, num_steps=8):
imgs = torch.stack([img1, img2], dim=0).to(model.device)
z, _ = model.encode(imgs)
alpha = torch.linspace(0, 1, steps=num_steps, device=z.device).view(-1, 1, 1, 1)
interpolations = z[0:1] * alpha + z[1:2] * (1 - alpha)
interp_imgs = model.sample(interpolations.shape[:1] + imgs.shape[1:], z_init=interpolations)
show_imgs(interp_imgs, row_size=8)
exmp_imgs, _ = next(iter(train_loader))
pl.seed_everything(42)
for i in range(2):
interpolate(flow_dict["vardeq"]["model"], exmp_imgs[2*i], exmp_imgs[2*i+1])

pl.seed_everything(42)
for i in range(2):
interpolate(flow_dict["multiscale"]["model"], exmp_imgs[2*i], exmp_imgs[2*i+1])

多尺度模型的插值会产生更真实的数字(第一行 7 ↔ 8 ↔ 6 7\leftrightarrow 8\leftrightarrow 6 7↔8↔6 、第二行 9 ↔ 6 9\leftrightarrow 6 9↔6 ),而变分反量化模型则侧重于全局不形成数字的局部模式。对于多尺度模型,我们实际上没有在两张图像之间进行 “真实 ”的插值,因为我们没有考虑沿流分割的变量(它们已对所有样本随机采样)。
1.6.4 多尺度潜在可视化的不同层次呈现
在这里我们将更多地关注多尺度流。这里主要想分析在早期层分割的变量中存储了哪些信息,以及最终变量存储了哪些信息。为此,我们对 8 张图像进行了采样,其中每张图像具有相同的最终潜在变量,但在潜在变量的另一部分有所不同。以下是三个示例:
pl.seed_everything(44)
for _ in range(3):
z_init = flow_dict["multiscale"]["model"].prior.sample(sample_shape=[1,8,7,7])
z_init = z_init.expand(8, -1, -1, -1)
samples = flow_dict["multiscale"]["model"].sample(img_shape=z_init.shape, z_init=z_init)
show_imgs(samples.cpu())


我们看到早期的 split 变量确实对图像的影响较小。尽管如此,当我们仔细观察数字的边界时,还是可以发现微小的差异。例如,在中间,3 的顶部对于不同的样品具有不同的厚度,尽管它们都代表相同的粗略结构。这表明 flow 确实学会了分离最终变量中的更高级别信息,而早期拆分的变量包含局部噪声模式。
1.6.5 反量化的可视化研究
最后我们将研究变分反量化的影响。我们通过尖锐的边缘/边界难以建模的问题来激发变分反量化,并且流更喜欢平滑的、类似先验的分布。为了检查变分反量化模块中的流是如何学习到什么噪声分布 q ( u ∣ x ) q(u|x) q(u∣x) 的,我们可以绘制一个来自反量化和变分反量化模块的输出值的直方图。
def visualize_dequant_distribution(model : ImageFlow, imgs : torch.Tensor, title:str=None):
"""
输入:
model:我们想要可视化其反量化分布的流模型
imgs:我们想要可视化其反量化分布的示例训练图像
"""
imgs = imgs.to(device)
ldj = torch.zeros(imgs.shape[0], dtype=torch.float32).to(device)
with torch.no_grad():
dequant_vals = []
for _ in tqdm(range(8), leave=False):
d, _ = model.flows[0](imgs, ldj, reverse=False)
dequant_vals.append(d)
dequant_vals = torch.cat(dequant_vals, dim=0)
dequant_vals = dequant_vals.view(-1).cpu().numpy()
sns.set()
plt.figure(figsize=(10,3))
plt.hist(dequant_vals, bins=256, color=to_rgb("C0")+(0.5,), edgecolor="C0", density=True)
if title is not None:
plt.title(title)
plt.show()
plt.close()
sample_imgs, _ = next(iter(train_loader))
visualize_dequant_distribution(flow_dict["vardeq"]["model"], sample_imgs, title="Variational dequantization")
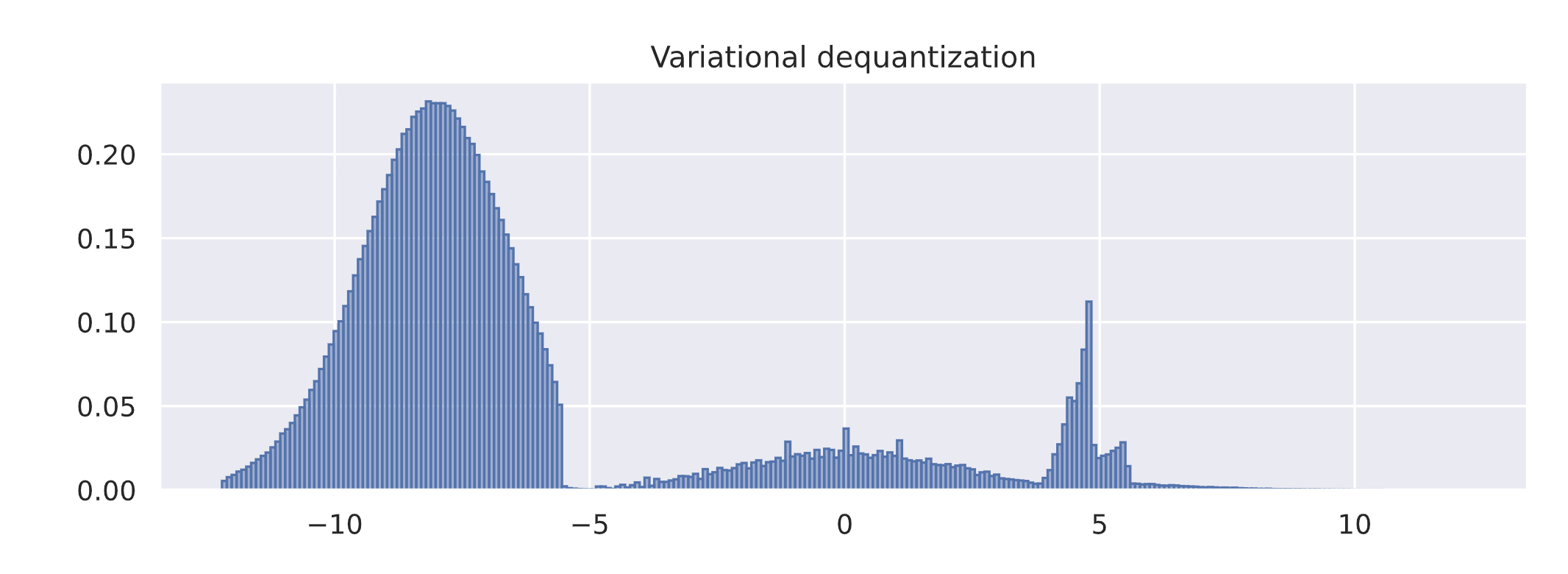
第一张图中的反量子分布表明,MNIST 图像对 0(黑色)有很强的偏差,并且如前所述,它们的分布具有明显的边界。变分反量化模块确实学习了更平滑的分布,具有类似高斯的曲线,可以更好地建模。对于其他值,我们需要在更深的层次上可视化分布 q ( u ∣ x ) q(u|x) q(u∣x),具体取决于 𝑥 𝑥 x。然而,由于所有 𝑢 𝑢 u 都相互作用并相互依赖,我们需要可视化 784 维的分布。
1.7 总结
总之,我们已经看到了如何实现我们自己的归一化流,以及如果我们想将它们应用于图像会出现哪些困难。反量子化是将离散图像映射到连续空间以防止低于 delta-peak 解的关键步骤。虽然反量化会创建具有硬边界的超立方体,但变分反量化使我们能够更好地拟合数据流。这允许我们获得较低的每维度 bits 分数,同时不影响采样速度。最常见的流元件,即耦合层,很容易实现,但很有效。此外,多尺度架构有助于捕获全局图像上下文,同时允许我们有效地扩展流。归一化流是 VAE 的一个有趣的替代方案,因为它们允许在连续空间中进行精确的似然估计,并且我们可以保证每个可能的输入 x x x 都有一个相应的潜在向量 z z z 。然而,即使在连续的输入和图像之外,也可以应用流,并允许我们利用潜在空间中的数据结构,例如在图表上完成分子生成的任务。
- PyTorch基础与异或问题实践
- 激活函数与神经网络优化
- 数据预处理与模型优化:FashionMNIST实验
- 经典CNN架构与PyTorch Lightning实践
- Transformers与多头注意力机制实战
- 深度能量模型与PyTorch实践
- 图神经网络
- 自编码器与神经网络应用
- 深度归一化流图像建模与实践
- 自回归图像建模与像素CNN实现
- Vision Transformers with PyTorch Lightning on昇腾
- ProtoNet与ProtoMAML元学习算法实践
- SimCLR与Logistic回归在自我监督学习中的应用





















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








