线性回归与高级回归模型实践：Robust Linear Regression 稳健线性回归

原创于 2025-10-29 16:44:11 发布 · 921 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#回归 #python #RobustLinear

Robust Linear Regression 稳健线性回归

学习目标

稳健线性回归（Robust Linear Regression）是一种改进型的线性回归分析方法，在这个实验中，我们使用了 scikit-learn 库中的 HuberRegressor 类来实现稳健线性回归。

学习内容

1 Robust Linear Regression算法进行线性回归

稳健线性回归（Robust Linear Regression）是一种改进型的线性回归分析方法，旨在处理数据中的异常值或离群点对模型的影响。传统最小二乘法对异常值非常敏感，可能导致估计结果偏差。稳健线性回归通过赋予不同数据点不同的权重来减轻这一问题，使得模型更加稳定可靠。稳健线性回归广泛应用于金融、经济学、社会科学等领域，在存在数据污染的情况下，它能够提供更准确的预测和参数估计，有助于构建更具解释力和实用性的统计模型。
稳健线性回归广泛应用于金融、经济学、社会科学等领域，在存在数据污染的情况下，它能够提供更准确的预测和参数估计，有助于构建更具解释力和实用性的统计模型。

1.1 导入包和数据集

import numpy as np
from sklearn.linear_model import HuberRegressor, LinearRegression
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

生成数据集

使用 make_regression 方法创建一个用于回归分析的合成数据集

make_regression 是 scikit-learn 提供的一个用于生成人工回归数据集的实用函数，能够快速创建可用于算法测试和教学演示的模拟数据。该函数允许用户自定义多个关键参数，包括样本数量（n_samples）、特征数量（n_features）、有效特征数（n_informative）以及目标值中的噪声水平（noise），从而灵活控制生成数据的复杂度。通过设置 bias 参数可以调整目标值的基线偏移，而 coef=True 时还能返回真实的回归系数用于结果验证。此外，random_state 参数确保每次生成的数据可复现。例如，调用 make_regression(n_samples=100, n_features=5) 会生成一个包含 100 个样本和 5 个特征的标准回归数据集，其中默认包含 10 个有效特征（若特征总数不足 10 则全部有效）。该函数特别适用于回归算法的基准测试、参数调优练习以及教学场景中的模型行为演示。

rng = np.random.RandomState(0)

X, y, coef = make_regression(
    n_samples=200, n_features=2, noise=4.0, 
    coef=True, random_state=0
)

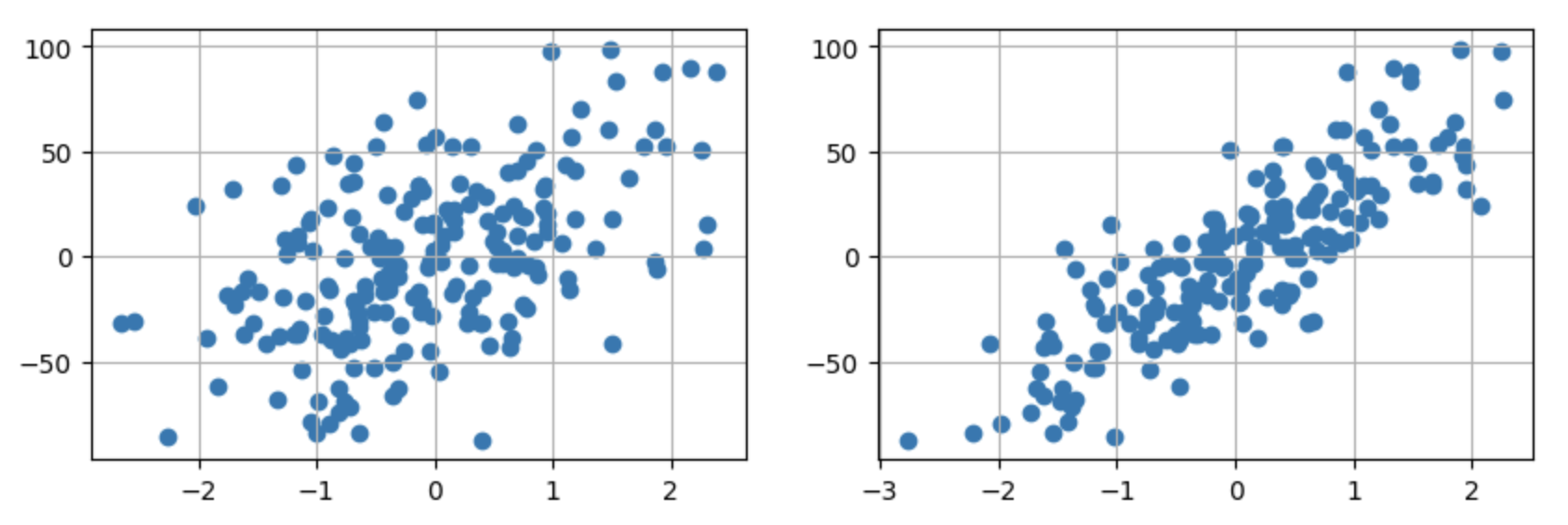
通过Plot图表展示数据

fix, ax = plt.subplots(1,2,figsize=(10,3))
ax[0].scatter(X[:,0],y)
ax[0].grid(True)
ax[1].scatter(X[:,1],y)
ax[1].grid(True)
plt.show()

在这里插入图片描述
插入随机值

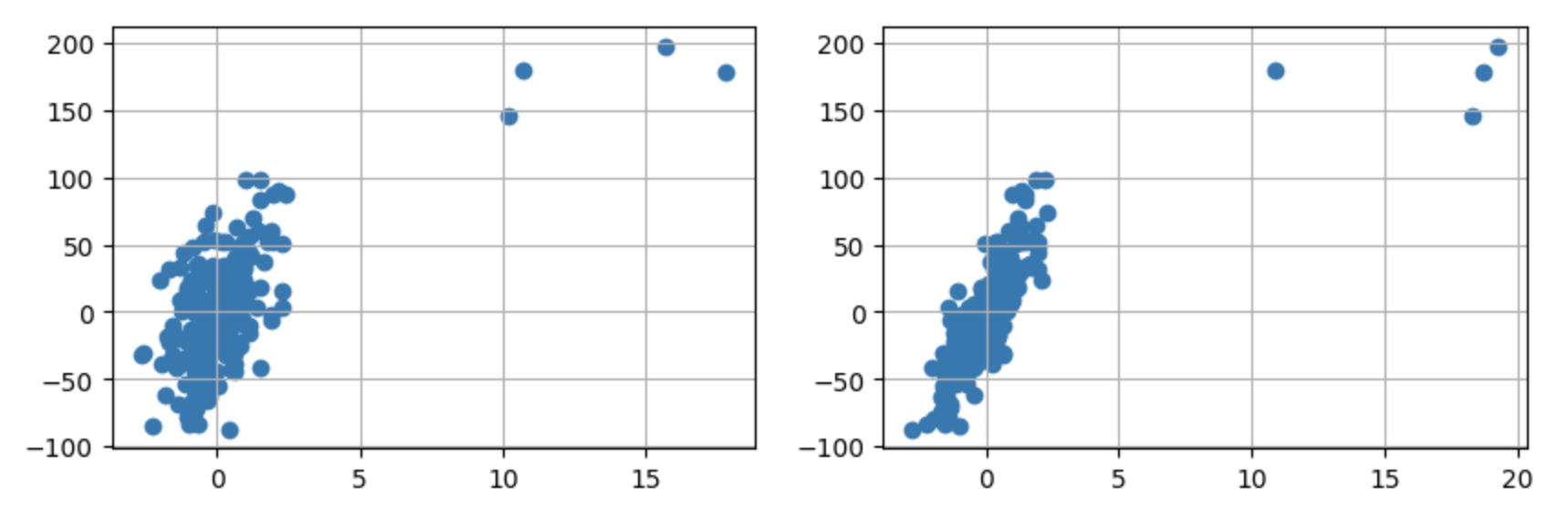
在数据中插入随机异常值

X[:4] = rng.uniform(10, 20, (4, 2))
y[:4] = rng.uniform(100, 200, 4)

绘制图表以显示插入的异常值

fix, ax = plt.subplots(1,2,figsize=(10,3))
ax[0].scatter(X[:,0],y)
ax[0].grid(True)
ax[1].scatter(X[:,1],y)
ax[1].grid(True)
plt.show()

在这里插入图片描述

1.2 数据拟合

Huber Regressor

Huber 回归器对满足 $∣y−X′wσ∣<ϵ|\frac{y - X'w}{\sigma}| < \epsilon$ 条件的样本优化平方损失，对满足 $∣y−X′wσ∣<ϵ|\frac{y - X'w}{\sigma}| < \epsilon$ 的样本则优化绝对值损失，其中 $w$ 和 $σ\sigma$ 是待优化的参数。

参数 $σ\sigma$ 确保即使因变量 $y$ 按一定比例放大或缩小，也不需要重新调整 epsilon 来维持相同的鲁棒性。需要注意的是，这种机制没有考虑自变量矩阵 $X$ 中的不同特征可能具有不同的尺度。

huber = HuberRegressor()
huber.fit(X,y)
X[1].reshape(1,-1)
huber.predict(X[1].reshape(1,-1))

线性回归

linear = LinearRegression()
linear.fit(X, y)

1.3 结果对比

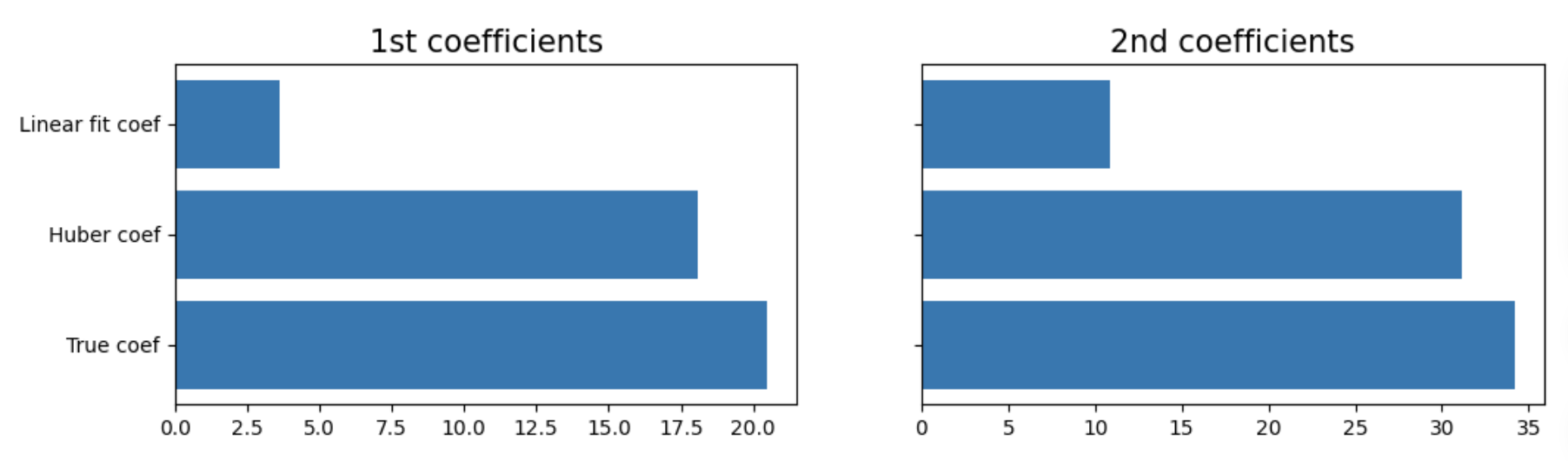
如下所示，Huber 回归器在存在异常值的情况下，估计的系数远比简单线性模型更准确（更接近真实值）。

print("True coefficients:", coef)
print("Huber coefficients:", huber.coef_)
print("Linear Regression coefficients:", linear.coef_)

Result：
True coefficients: [20.4923687 34.16981149]
Huber coefficients: [18.10608481 31.16559039]
Linear Regression coefficients: [ 3.63326689 10.82594129]

fix, ax = plt.subplots(1,2,figsize=(12,3),sharey=True)
ax[0].barh(['True coef','Huber coef', 'Linear fit coef'],width=[coef[0],huber.coef_[0],linear.coef_[0]])
ax[0].set_title("1st coefficients",fontsize=15)
ax[1].barh(['True coef','Huber coef', 'Linear fit coef'],width=[coef[1],huber.coef_[1],linear.coef_[1]])
ax[1].set_title("2nd coefficients",fontsize=15)
plt.show()