线性回归与高级回归模型实践：支持向量回归的实现方法-优快云博客

支持向量回归的实现方法

学习目标

通过本课程，我们了解支持向量回归的建模流程，包括数据预处理、模型训练与参数优化等关键环节，从而深入理解其在解决回归问题中的应用效果。

学习内容

1. 支持向量回归的实现方法

1.1 导入相关库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

1.2 创建数据

以下是一个简单的非线性函数，用于生成不适合线性回归模型的合成数据。我们将通过该数据集展示支持向量回归器在提升预测性能方面的优势。

def nonlinear(array):
    return (10*array[:,0]-np.exp(0.01*array[:,1]+np.log(1+array[:,2]**2)))/(array[:,3]**2+5)

1.2.1 生成回归的特征和目标数据

n_samples：表示数据集中样本的数量，每个样本可以是一个观测值、一个实例或一个记录，具体取决于应用场景。
n_features：表示每个样本的特征数量，特征可以是数值型或分类型变量，具体取决于数据的性质。
生成一个形状为 (n_samples, n_features) 的随机矩阵 X，其元素服从 [0, 1) 均匀分布，并通过线性变换将数值范围调整至 [0, 5) 区间。
构造目标变量 y 作为特征矩阵 X 的非线性变换 nonlinear(X) 与随机噪声的叠加：

n_samples = 200
n_features = 4

x = 5*np.random.rand(n_samples,n_features)

y = nonlinear(x)+np.random.randn(n_samples)
y=y.reshape(n_samples,1)
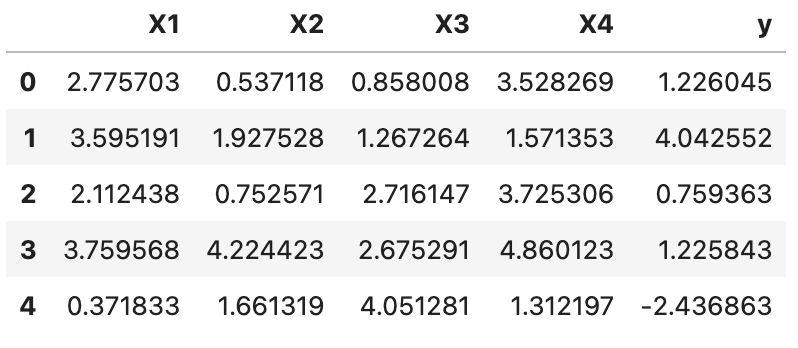
df = pd.DataFrame(data=np.hstack((x,y)),columns=['X1','X2','X3','X4','y'])
df.head()

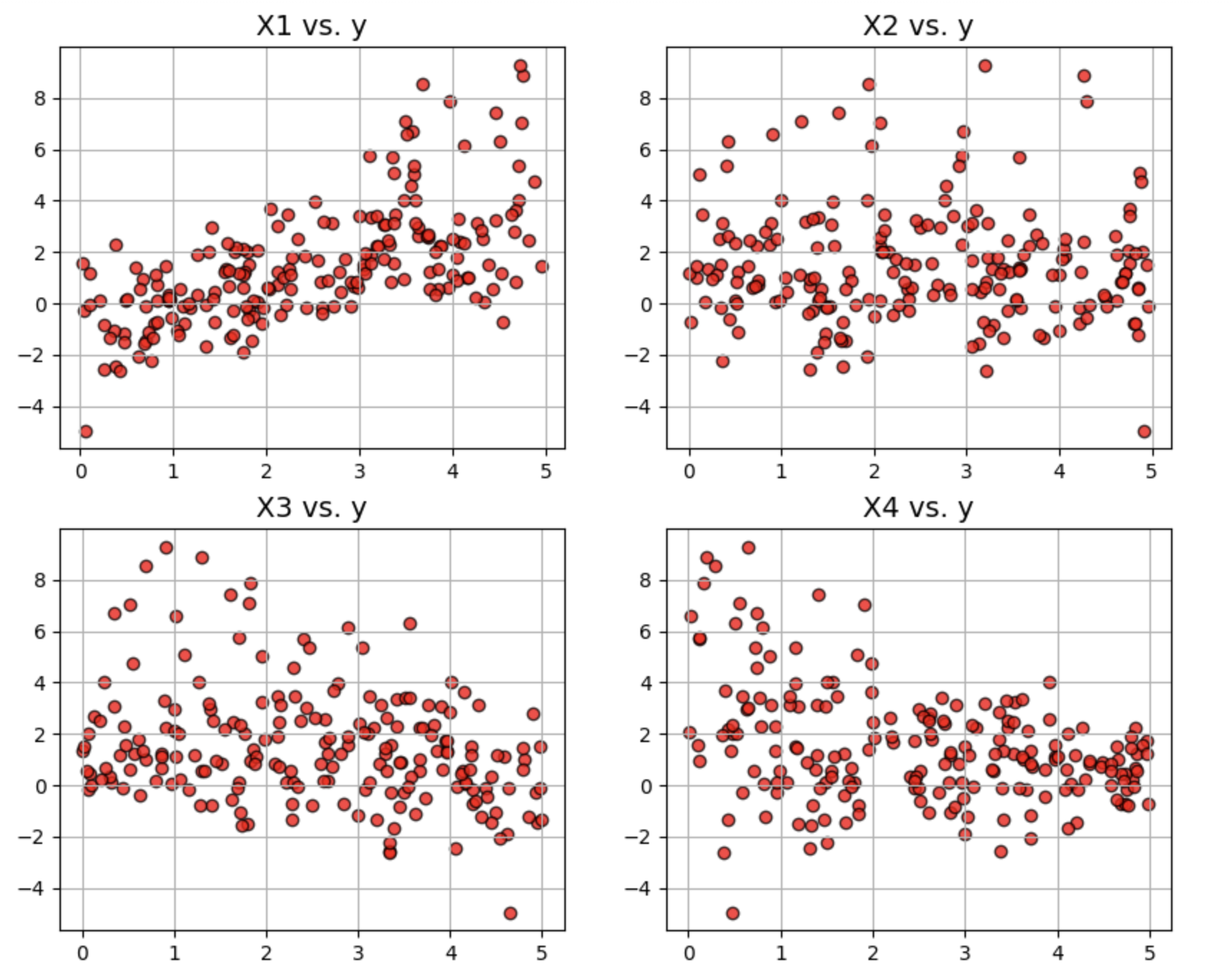
在这里插入图片描述

1.3 绘制数据

fig,ax = plt.subplots(2,2,figsize=(10,8))
ax = ax.ravel()
for i in range(4):
    ax[i].scatter(df[df.columns[i]],df['y'],edgecolor='k',color='red',alpha=0.75)
    ax[i].set_title(f"{df.columns[i]} vs. y",fontsize=14)
    ax[i].grid(True)
plt.show()

在这里插入图片描述

1.4 模型训练

1.4.1 测试/训练数据拆分

训练集和测试集的比例2：1

from sklearn.model_selection import train_test_split

X = df[['X1','X2','X3','X4']]
y = df['y']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

1.4.2 模型拟合

使用线性内核的支持向量回归器（SVR）。

from sklearn.svm import SVR
svr_linear = SVR(kernel='linear',gamma='scale', C=1.0, epsilon=0.1)
svr_linear.fit(X_train, y_train)

1.4.3 模型测试

测试分数的计算结果：

svr_linear.score(X_test,y_test)

以线性回归模型作为基准进行比较。

from sklearn.linear_model import LinearRegression

linear = LinearRegression()
linear.fit(X_train,y_train)
linear.score(X_test,y_test)

支持高斯（径向基函数，RBF）内核的向量回归器。

svr_rbf = SVR(kernel='rbf',gamma='scale', C=1.0, epsilon=0.1)
svr_rbf.fit(X_train, y_train) 

svr_rbf.score(X_test,y_test)

Output：
0.6569634611276103
结果表明，RBF 内核在测试集上显示出更高的准确性。

from sklearn.metrics import mean_squared_error
print("RMSE for linear SVR:",np.sqrt(mean_squared_error(y_test,svr_linear.predict(X_test))))
print("RMSE for RBF kernelized SVR:",np.sqrt(mean_squared_error(y_test,svr_rbf.predict(X_test))))

Result：
RMSE for linear SVR: 1.443714899500632
RMSE for RBF kernelized SVR: 1.242833491827153

1.5 模型调优

网格搜索

网格搜索（Grid Search）是一种用于机器学习模型超参数优化的方法，通过系统地遍历预定义的参数组合，结合交叉验证来评估每个参数组合的性能，从而找到最优的超参数设置。这种方法的核心在于穷举搜索，即对所有可能的参数组合进行评估，以确保找到最佳的模型配置。
在实际应用中，网格搜索通常与交叉验证结合使用，以提高模型评估的稳健性。具体步骤包括：定义参数网格、设置交叉验证策略、初始化模型、遍历参数组合并评估模型性能，最终选择表现最好的参数组合。虽然网格搜索能够系统地找到最优参数，但其计算成本较高，尤其是当参数空间较大时。因此，对于大规模问题，可能会考虑使用随机搜索等替代方法。

我们可以对超参数进行网格搜索（使用 5 倍交叉验证）以查看测试 / 验证分数是否有所提高

from sklearn.model_selection import GridSearchCV

params = {'C':[0.01,0.05,0.1,0.5,1,2,5],'epsilon':[0.1,0.2,0.5,1]}
grid = GridSearchCV(svr_rbf,param_grid=params,cv=5,scoring='r2',verbose=1,return_train_score=True)

grid.fit(X_train,y_train)

Output：
Fitting 5 folds for each of 28 candidates, totalling 140 fits
在这里插入图片描述
检查网格搜索认为的最佳估计器：可以通过 best_estimator_ 属性获取。

grid.best_estimator_

使用训练数据拟合估计器参数，然后通过测试集评估模型表现

svr_best=SVR(kernel='rbf',gamma='scale', C=5.0, epsilon=0.5)
svr_best.fit(X_train, y_train)

svr_best.score(X_test,y_test)

out：
0.7157250700707216

print("RMSE for RBF kernelized SVR:",np.sqrt(mean_squared_error(y_test,svr_best.predict(X_test))))

Out：
RMSE for RBF kernelized SVR: 1.1313892235060616