模拟下变频与采样 通俗讲解 一图搞懂

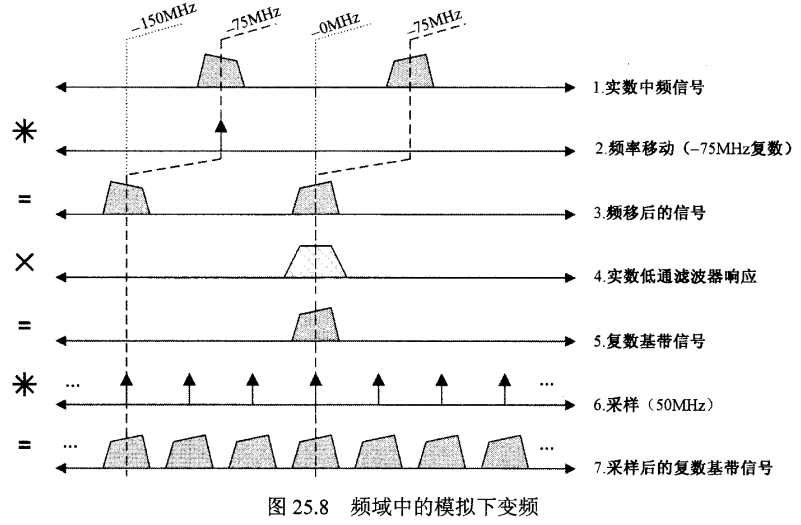
        如图25.8中频域所示，数字下变频的一般方法源自模拟下变频和采样。第1行和“=”
行上的频谱表示系统中不同节点上的信号，“*”行和“x”行上的频谱分别表示把那些把信
号相关起来的频谱卷积以及逐点频谱相乘运算。
        图中第1行画出了一个实数中频（IF）信号示意图，这个信号的单边带宽和双边带宽分
别为40MHz和80MHz，正频率分量和负频率分量的中心分别位于75MHz和-75MHz。图25.8
中的第二行用一个-75MHz的本振频率通过频谱卷积将中频信号频移（很快我们将看到这是
如何用硬件实现的）。第3行上的结果的频率分量中心位于0Hz和-150MHz。与第4行中的
低通滤波器频率响应相乘，于是去除了-150MHz的分量，只留下第5行的复数基带信号，这
个信号有一个双边带宽和40MHz的奈奎斯特频率。第6行上的频率卷积对应于在时域上将
第5行表示的信号与一个以50MHz采样频率采样的均匀脉冲序列相乘。在时域中，结果就是
一个50MHz的采样脉冲序列，其值是第5行信号在采样时刻的采样值（我们忽略比例因子)。
当然，我们在硬件中不会生成第7行中的脉冲，而是在寄存器中以数来数字地实现脉冲区域。

通俗解释就是：

第 1 行 — 实数中频（IF）信号：两个对称的频谱包

• 图 1 行画的是一个实值中频信号的频谱。实信号在频域总是成对出现：正频率分量和负频率分量是对称的。

• 在图中，这两个“包”各自围绕 +75 MHz 和 −75 MHz 展开（两侧合起来是“总带宽”）。

• 比喻：就像频谱在 +75 和 −75 两个地方各站了一群人（能量），每群人占一定宽度（带宽）。

---

第 2 行 — 用本振（LO）把频谱“搬走”（频率变移 / 混频）

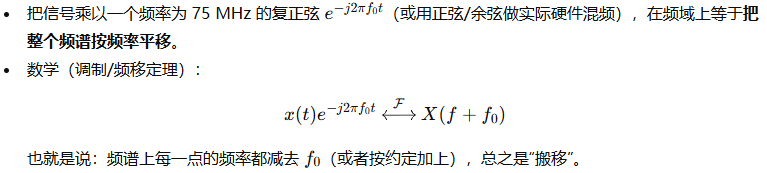
• 在图里把中心在 +75MHz 的那一群移动到 0Hz（基带），而原来在 −75MHz 的那一群被移动到 −150MHz。于是频谱变成了两个新的“包”：一个在 0Hz，另一个在 −150MHz（第 3 行所示结果）。

---

第 3 → 第 4 行 — 用低通滤波器去掉远处的“镜像”

• 现在你有两个“包”：靠近 0 的包（有价值）和远在 −150MHz 的包（镜像 / 图像成分）。

• 把信号通过低通滤波器（LPF），可以把靠近 0 的包保留下来，去掉远处的 −150MHz 包。
  这是经典的去除混频后“镜像频谱”的做法。

• 结果是第 5 行：只剩下靠近 0Hz 的那部分 —— 这就是复数基带信号（complex baseband）。

---

第 5 行 — 复数基带信号（把频谱移到 0 附近）

• 剩下的信号称为复数基带，它在中心 0 附近对称展开（即双边带围绕 0）。

• 复数基带的好处：带通信息被“搬到”低频（便于数字处理），而且 I/Q 能区分正负频率信息（防止二义性）。

---

第 6 行 — 采样在频域就是把频谱“复制”成很多份

---

第 7 行 — 在时域上看采样：用脉冲“挑取”取样点

• 

• 在实际数字系统中，我们不会物理上产生窄脉冲把模拟信号“打孔”，而是用 ADC（模数转换器）在时刻把值读入寄存器；数学上等价于乘以冲激列。

• 第 7 行就是展示了被采样后的离散脉冲序列的频谱（每个脉冲代表一个采样值），以及在寄存器中以数字形式保存的效果。

---

为什么要先下变频再采样？

1. 把高频信息搬到低频，便于用较低速率的 ADC 采样（节省硬件资源）或降低后续数字处理的计算量。

2. 用低通滤波去掉镜像，可以得到干净的基带（避免 aliasing）。

3. IQ（复数基带）能保留相位信息，这是很多通信 / 雷达处理不可或缺的（例如相位解调、方位信息等）。

---

常见的两种实现方式（硬件上）

• 直接射频复数下变频（IQ 混频）→ 低通 → ADC 采样基带：这是现代接收机常见形式，能得到复数基带直接供数字处理。

• 先用实 LO 混频成低频再用 LPF → ADC：如果仅用实余弦作 LO，会产生对称镜像，必须滤掉；适用于只需要功率或幅值的场合。

---

小结

1. 图中先把 IF 的频谱“搬移”（混频）使有用部分落到 0 附近；

2. 再用低通滤波把不需要的镜像去掉，得到复数基带；

3. 最后用采样（ADC）把连续时间基带变成离散时间序列——在频域上采样会把基带频谱周期性复制（所以设计采样率和滤波器时要注意避免频谱重叠 / 折叠）。

代码实现及可视化

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

"""
IF -> IQ 混频 -> LPF -> 采样 仿真（中文注释与绘图）
保存图像为 PNG 并在终端打印参数说明（中文）。

依赖：
    pip install numpy matplotlib

用法：
    python if_iq_sim_chinese.py

注意：
    - 脚本会尝试在系统字体中选择常见中文字体（SimHei、Noto Sans CJK、WenQuanYi 等）。
      如果系统没有中文字体，matplotlib 可能无法正确显示中文文字；脚本会打印提示并继续运行。
    - 可修改脚本顶部的参数来改变采样率、带宽、SNR 等。
"""

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import font_manager
import os

# ------------------ 参数区（可调整） ------------------
# 内部“模拟”采样率（用于离散化连续时间以做 FFT / 仿真）
fs_cont = 500e6       # Hz
duration = 1e-4       # 秒
N = int(np.round(fs_cont * duration))
t = np.arange(N) / fs_cont

f_center = 75e6       # 中频中心频率 +75 MHz
bandwidth = 40e6      # 信号带宽（双边带总宽度），Hz
half_bw = bandwidth / 2

Fs = 50e6             # ADC 采样率（最终采样率），Hz
decim = int(np.round(fs_cont / Fs))
if decim < 1:
    decim = 1

SNR_dB = 20.0         # 添加噪声的目标 SNR (dB)

# LPF 截止频率（单位：Hz），建议 <= Fs/2（留有过渡带）
lpf_cutoff = 25e6

# 输出图像保存目录
out_dir = "sim_plots"
os.makedirs(out_dir, exist_ok=True)

# ------------------ 自动选择中文字体 ------------------
def choose_chinese_font():
    # 常见中文字体候选（名称或文件名中匹配）
    candidates = [
        "SimHei", "SimSun", "Noto Sans CJK", "NotoSansCJK", "WenQuanYi", "AR PL", "Microsoft YaHei",
        "PingFang", "Heiti SC", "STHeiti", "Source Han Sans", "SourceHanSans", "Noto Sans CJK SC",
        "Arial Unicode MS"
    ]
    sys_fonts = font_manager.findSystemFonts(fontpaths=None, fontext='ttf')
    sys_names = [font_manager.FontProperties(fname=f).get_name() for f in sys_fonts]
    # 尝试按优先候选匹配系统字体名称
    for cand in candidates:
        for idx, name in enumerate(sys_names):
            if cand.lower() in name.lower():
                return sys_fonts[idx], name
    # 如果没有候选，尝试返回第一个系统字体
    if sys_fonts:
        return sys_fonts[0], font_manager.FontProperties(fname=sys_fonts[0]).get_name()
    return None, None

font_path, font_name = choose_chinese_font()
if font_path:
    try:
        matplotlib.rcParams['font.sans-serif'] = [font_name]
        matplotlib.rcParams['font.family'] = 'sans-serif'
        matplotlib.rcParams['axes.unicode_minus'] = False
        font_notice = f"已选用系统字体：{font_name}（文件：{os.path.basename(font_path)}）"
    except Exception:
        font_notice = "尝试设置中文字体失败，仍使用 matplotlib 默认字体显示。"
else:
    font_notice = ("未在系统中找到可识别的字体。若中文不能正常显示，"
                   "请在系统中安装常见中文字体（例如 SimHei、Noto Sans CJK、WenQuanYi 或 Microsoft YaHei）。")
print(font_notice)

# ------------------ 构造实值 IF 信号（在频域直接造谱以便控制形状） ------------------
freqs = np.fft.fftshift(np.fft.fftfreq(N, d=1/fs_cont))
Spec = np.zeros(N, dtype=complex)

# 在 +75 MHz 附近创建一个宽带平顶谱（示意）
mask_plus = np.logical_and(freqs >= (f_center - half_bw), freqs <= (f_center + half_bw))
# 由实信号对称，负频谱为共轭镜像
np.random.seed(2)
Spec[mask_plus] = np.exp(1j*2*np.pi*np.random.rand(mask_plus.sum()))
Spec[np.logical_and(freqs <= (-f_center + half_bw), freqs >= (-f_center - half_bw))] = np.conj(Spec[mask_plus])

# 变回时域（确保为实信号）
sig_if = np.real(np.fft.ifft(np.fft.ifftshift(Spec))) * N
sig_if = sig_if / np.std(sig_if)  # 归一化信号功率为 1

# ------------------ IQ 混频（复数 LO） ------------------
lo = np.exp(-1j * 2 * np.pi * f_center * t)  # 复数 LO：把 +f_center 下移到 0
sig_mixed = sig_if * lo  # 结果为复数（I + jQ）

# ------------------ 加 AWGN（根据指定 SNR） ------------------
power_sig = np.mean(np.abs(sig_mixed)**2)
SNR_linear = 10**(SNR_dB / 10.0)
noise_power = power_sig / SNR_linear
noise = np.sqrt(noise_power/2) * (np.random.randn(N) + 1j*np.random.randn(N))
sig_mixed_noisy = sig_mixed + noise

# ------------------ 低通滤波器（FIR 窗口化 sinc） ------------------
num_taps = 801  # 滤波器 taps（越大过渡带越窄，但计算量增大）
m = np.arange(num_taps) - (num_taps - 1) / 2
fc_norm = lpf_cutoff / fs_cont  # 截止频率相对于采样率
h = 2 * fc_norm * np.sinc(2 * fc_norm * m)
h *= np.hamming(num_taps)
h /= np.sum(h)

# 卷积滤波（same 长度）
sig_filtered = np.convolve(sig_mixed_noisy, h, mode='same')

# ------------------ 采样（降采样 / 抽取） ------------------
sig_sampled = sig_filtered[::decim]
fs_sampled = fs_cont / decim
t_sampled = np.arange(len(sig_sampled)) / fs_sampled

# ------------------ 频谱绘图辅助函数（中文注释） ------------------
def plot_spectrum_save(x, fs, title, filename, xlim_mhz=300, ref_max_db=0):
    """
    绘制并保存频谱图
    - x: 信号（可以为复数）
    - fs: 采样率（Hz）
    - title: 图标题（中文）
    - filename: 保存文件路径
    """
    Nfft = len(x)
    X = np.fft.fftshift(np.fft.fft(x))
    mag = 20 * np.log10(np.abs(X) + 1e-12)
    mag = mag - np.max(mag) + ref_max_db  # 以峰值为参考
    freqs_mhz = np.fft.fftshift(np.fft.fftfreq(Nfft, d=1.0/fs)) / 1e6

    plt.figure(figsize=(10,4))
    plt.plot(freqs_mhz, mag, linewidth=1)
    plt.xlim(-xlim_mhz, xlim_mhz)
    plt.ylim(-80, 5)
    plt.grid(True, linestyle=':')
    plt.xlabel("频率 / MHz")
    plt.ylabel("幅度 / dB（相对于峰值）")
    plt.title(title)
    # 添加图中文字体说明（若字体可用）
    plt.tight_layout()
    plt.savefig(filename, dpi=200)
    plt.close()

def plot_time_save(t_axis, x, title, filename, samples_to_plot=800):
    plt.figure(figsize=(10,3))
    n = min(samples_to_plot, len(x))
    # 若是复数，绘制实部与虚部
    if np.iscomplexobj(x):
        plt.plot(t_axis[:n]*1e6, x[:n].real, label='实部')
        plt.plot(t_axis[:n]*1e6, x[:n].imag, label='虚部', alpha=0.8)
    else:
        plt.plot(t_axis[:n]*1e6, x[:n], label='波形')
    plt.xlabel("时间 / 微秒")
    plt.ylabel("幅度")
    plt.title(title)
    plt.legend()
    plt.grid(True, linestyle=':')
    plt.tight_layout()
    plt.savefig(filename, dpi=200)
    plt.close()

# ------------------ 保存图像 ------------------
# 1) 原始 IF 频谱（连续模拟仿真）
plot_spectrum_save(sig_if, fs_cont, "1) 原始实值 IF 频谱（±75 MHz）", os.path.join(out_dir, "01_if_spectrum.png"), xlim_mhz=300)

# 2) IQ 混频后（+75 MHz → 0Hz）
plot_spectrum_save(sig_mixed, fs_cont, "2) IQ 混频后（将 +75 MHz 下移到 0 Hz）", os.path.join(out_dir, "02_mixed_spectrum.png"), xlim_mhz=300)

# 3) 混频并加噪
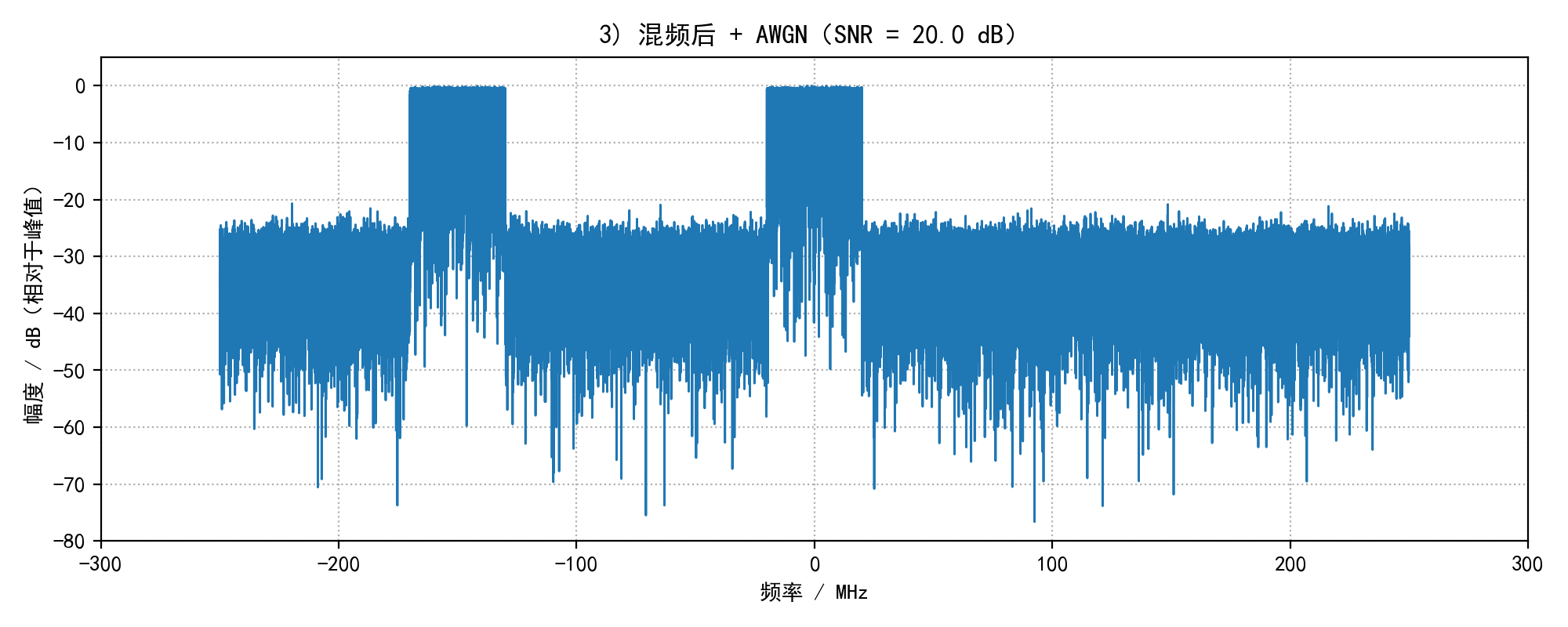
plot_spectrum_save(sig_mixed_noisy, fs_cont, f"3) 混频后 + AWGN（SNR = {SNR_dB} dB）", os.path.join(out_dir, "03_mixed_noisy_spectrum.png"), xlim_mhz=300)

# 4) 低通滤波后（复基带）
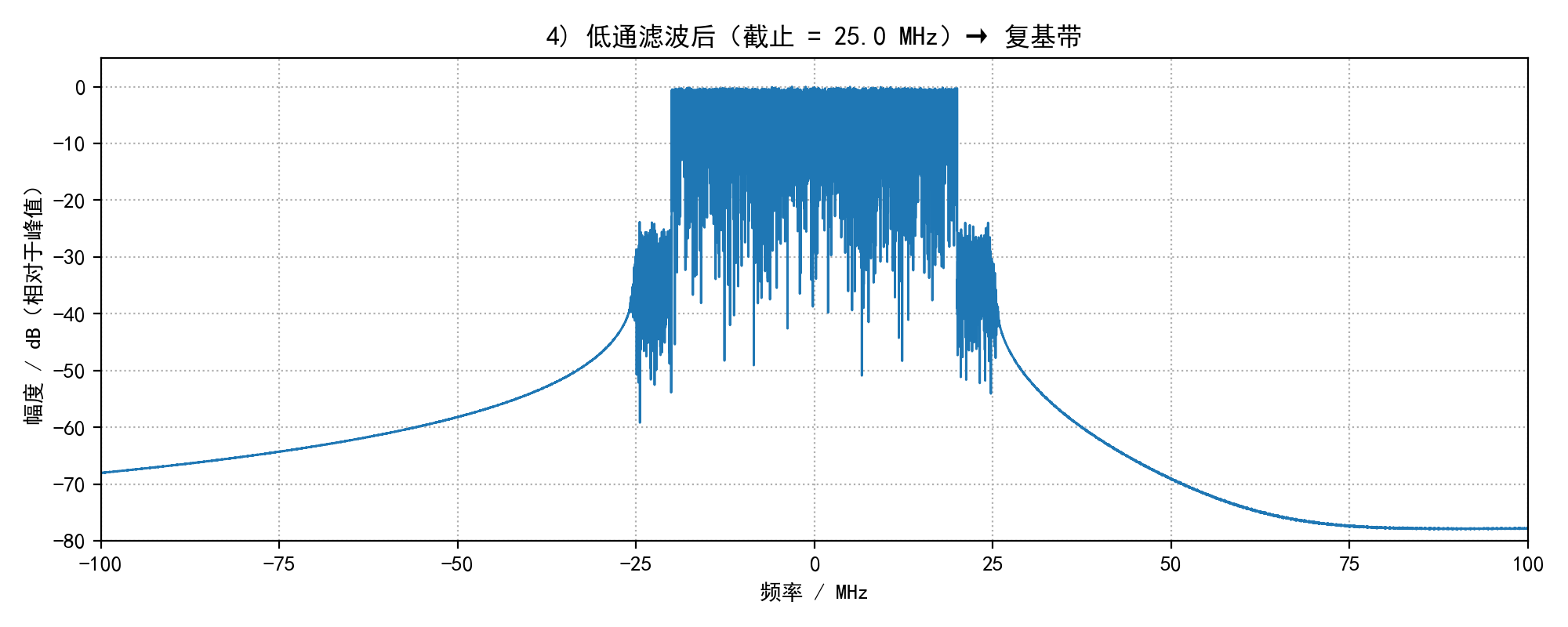
plot_spectrum_save(sig_filtered, fs_cont, f"4) 低通滤波后（截止 = {lpf_cutoff/1e6:.1f} MHz）→ 复基带", os.path.join(out_dir, "04_filtered_spectrum.png"), xlim_mhz=100)

# 5) 采样后（显示重复谱）
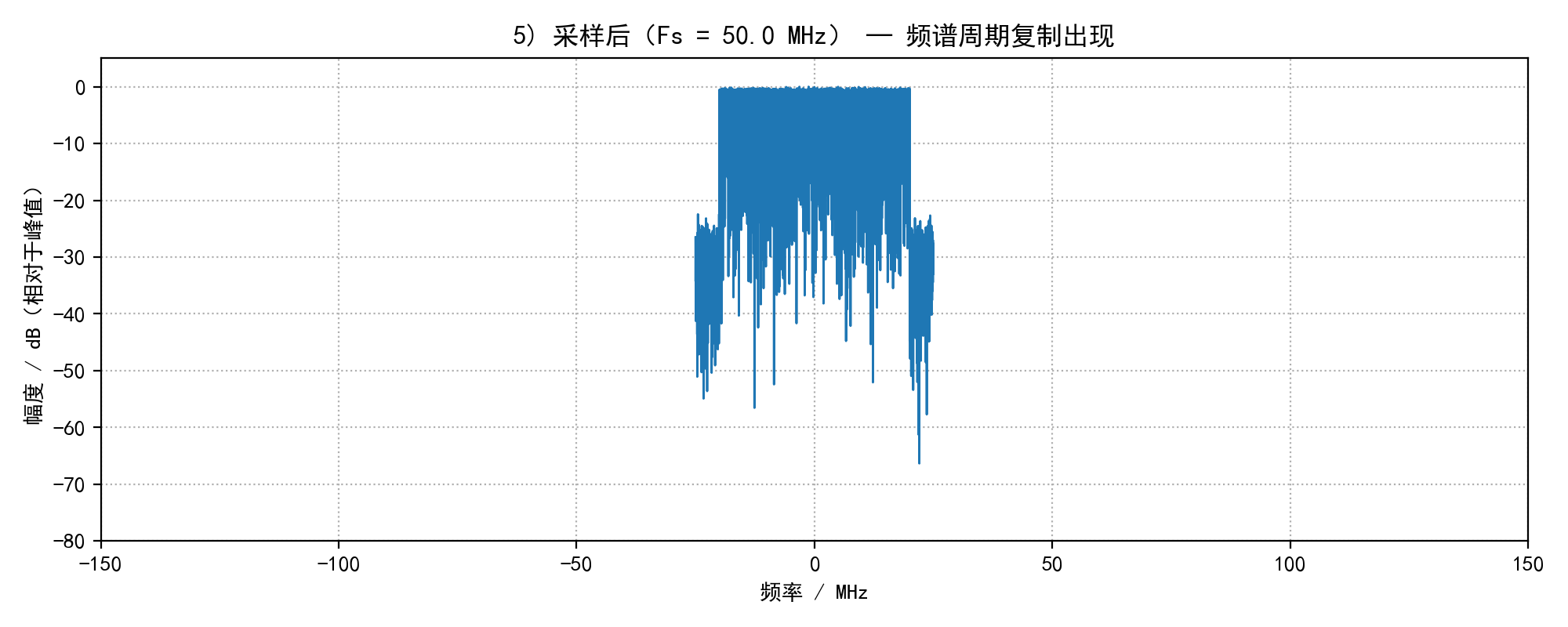
plot_spectrum_save(sig_sampled, fs_sampled, f"5) 采样后（Fs = {fs_sampled/1e6:.1f} MHz） — 频谱周期复制出现", os.path.join(out_dir, "05_sampled_spectrum.png"), xlim_mhz=150)

# 6) 时域波形快照：原始 IF、混频后、采样后
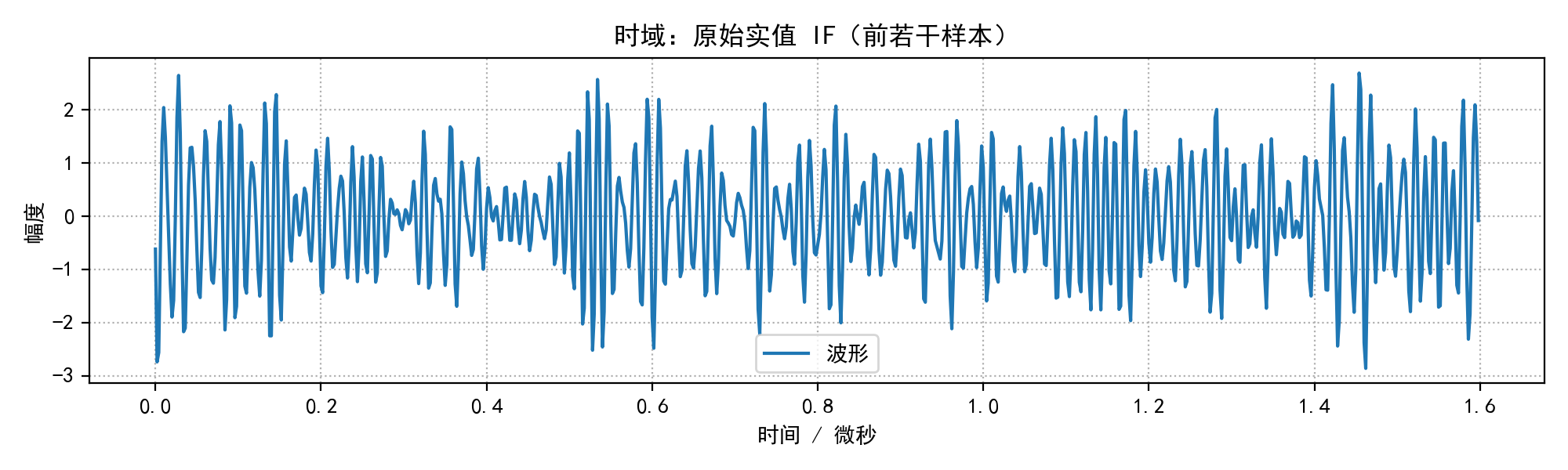
plot_time_save(t, sig_if, "时域：原始实值 IF（前若干样本）", os.path.join(out_dir, "time_if.png"))
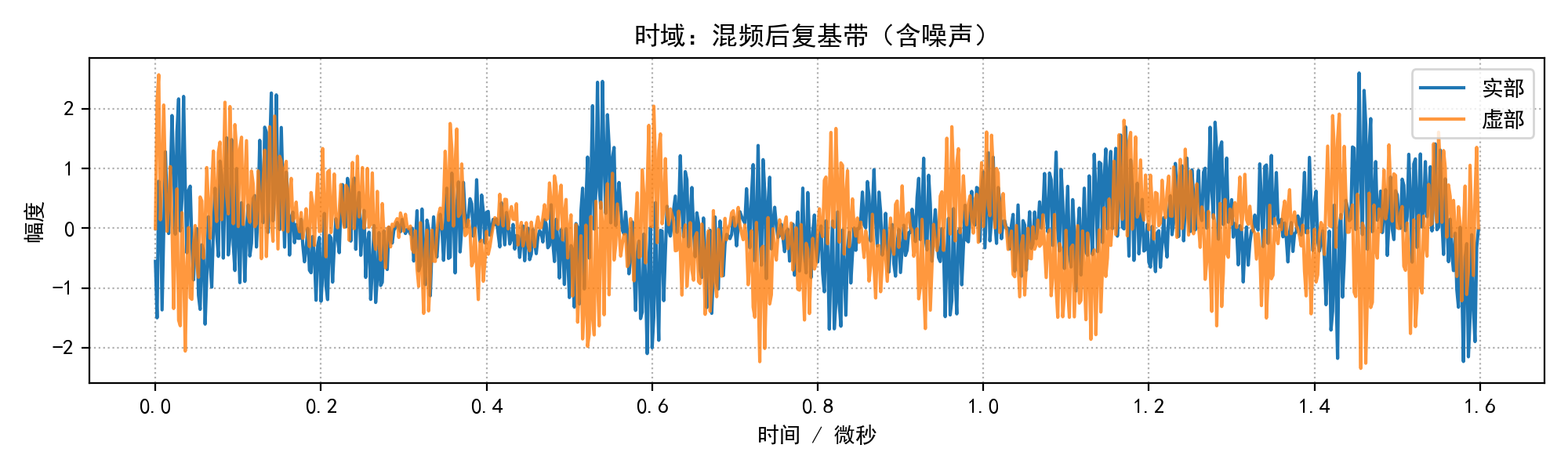
plot_time_save(t, sig_mixed_noisy, "时域：混频后复基带（含噪声）", os.path.join(out_dir, "time_mixed_noisy.png"))
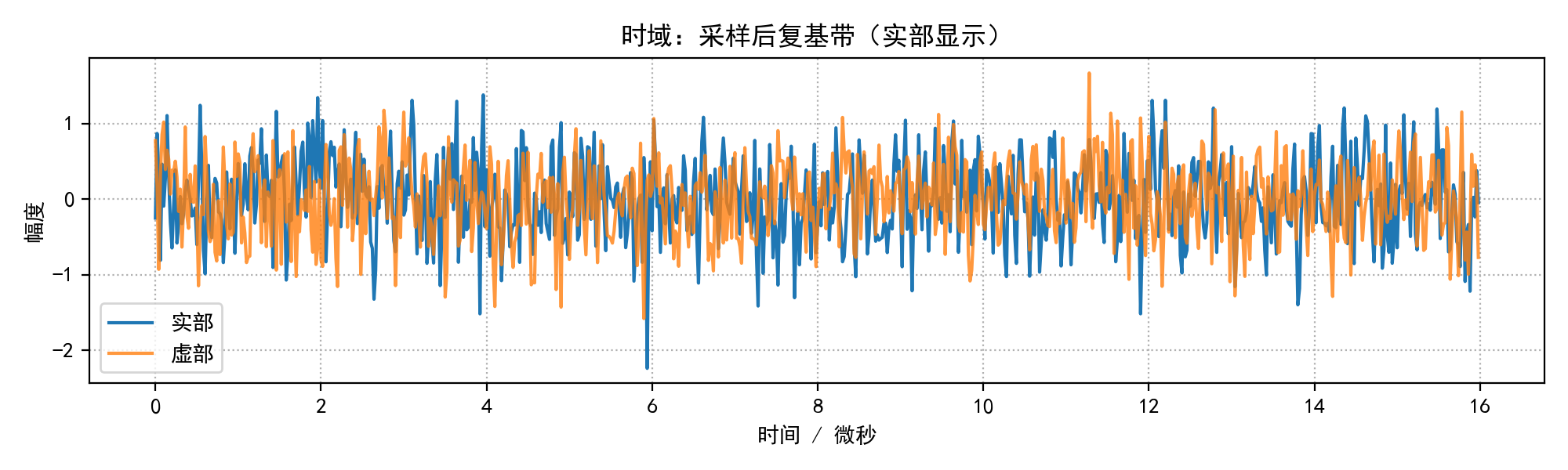
plot_time_save(t_sampled, sig_sampled, "时域：采样后复基带（实部显示）", os.path.join(out_dir, "time_sampled.png"))

# ------------------ 打印参数与说明（中文） ------------------
print("仿真参数（中文说明）：")
print("--------------------------------------------")
print(f"内部等效采样 fs_cont = {fs_cont/1e6:.1f} MHz，仿真样本数 N = {N}")
print(f"IF 中心频率 f_center = {f_center/1e6:.1f} MHz，信号带宽 = {bandwidth/1e6:.1f} MHz（双边带）")
print(f"目标 ADC 采样率 Fs = {Fs/1e6:.1f} MHz，抽取因子 decim = {decim}，实际采样率 fs_sampled = {fs_sampled/1e6:.3f} MHz")
print(f"LPF 截止频率 = {lpf_cutoff/1e6:.1f} MHz，FIR taps = {num_taps}")
print(f"添加噪声的 SNR = {SNR_dB:.1f} dB（参考混频后信号功率）")
print("")
print(f"图像已保存到目录：{os.path.abspath(out_dir)}")
print("主要图像文件：")
for fn in sorted(os.listdir(out_dir)):
    print("  -", fn)
print("")
print("说明：")
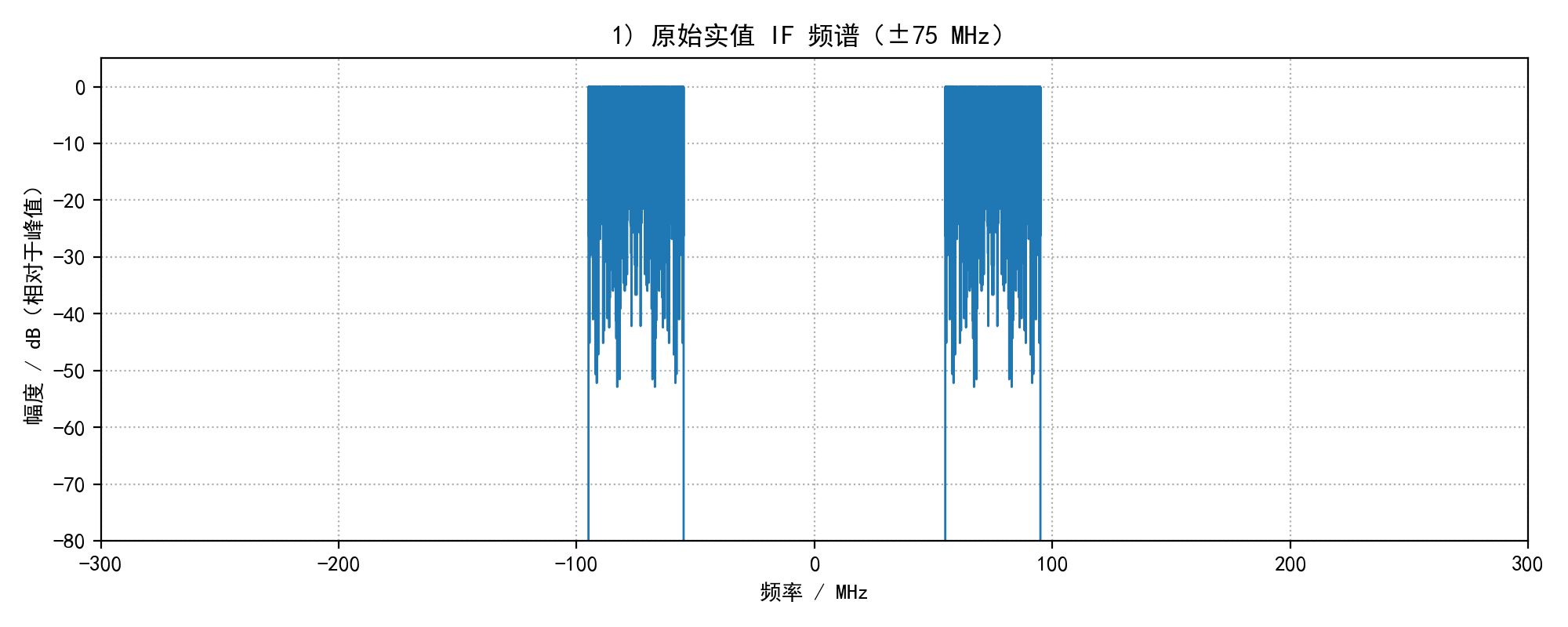
print("  1) 原始 IF（实值）在频域表现为 ±75 MHz 对称的两个带（对应书中第 1 行）。")
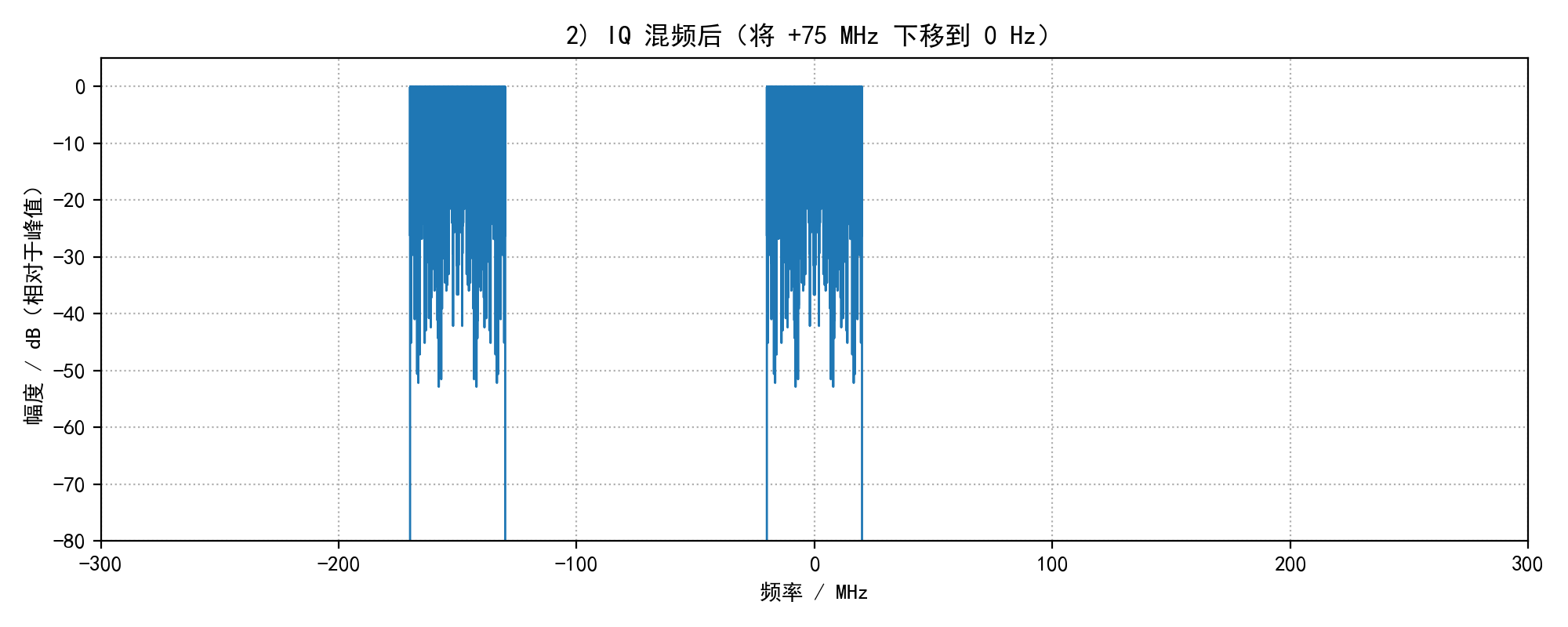
print("  2) IQ 混频相当于把 +75 MHz 带下移到 0 Hz，负频谱部分会被移到 -150 MHz（对应书中第 2、3 行）。")
print("  3) 低通滤波会保留靠近 0 的基带，去掉远处的镜像（对应书中第 4、5 行）。")
print("  4) 采样会在频域产生每 Fs 周期的谱复制（对应书中第 6、7 行）；若 LPF 过宽或 Fs 过低会造成频谱重叠（混叠）。")
print("")
print("如果需要：")
print("  - 我可以把脚本改为在绘图窗口直接弹出显示（交互式），或把每张图的分辨率 / 轴范围 / LPF 参数进一步调优。")
print("  - 或者我可以把脚本改为 Jupyter + ipywidgets 交互版，实时调整 SNR、Fs、LPF 截止等参数。")

运行结果

仿真参数（中文说明）：
--------------------------------------------
内部等效采样 fs_cont = 500.0 MHz，仿真样本数 N = 50000
IF 中心频率 f_center = 75.0 MHz，信号带宽 = 40.0 MHz（双边带）
目标 ADC 采样率 Fs = 50.0 MHz，抽取因子 decim = 10，实际采样率 fs_sampled = 50.000 MHz
LPF 截止频率 = 25.0 MHz，FIR taps = 801
添加噪声的 SNR = 20.0 dB（参考混频后信号功率）

图像已保存到目录：D:\workplace\LLM\sim_plots
主要图像文件：
  - 01_if_spectrum.png
  - 02_mixed_spectrum.png
  - 03_mixed_noisy_spectrum.png
  - 04_filtered_spectrum.png
  - 05_sampled_spectrum.png
  - time_if.png
  - time_mixed_noisy.png
  - time_sampled.png

说明：
  1) 原始 IF（实值）在频域表现为 ±75 MHz 对称的两个带（对应书中第 1 行）。
  2) IQ 混频相当于把 +75 MHz 带下移到 0 Hz，负频谱部分会被移到 -150 MHz（对应书中第 2、3 行）。
  3) 低通滤波会保留靠近 0 的基带，去掉远处的镜像（对应书中第 4、5 行）。
  4) 采样会在频域产生每 Fs 周期的谱复制（对应书中第 6、7 行）；若 LPF 过宽或 Fs 过低会造成频谱重叠（混叠）。

运行可视化