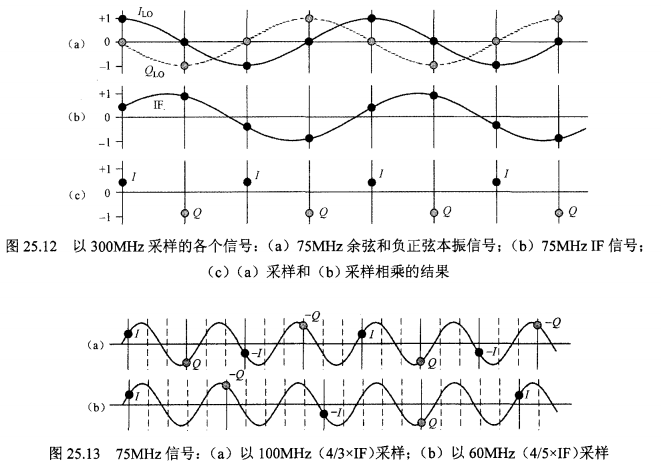
第一步:图 25.12 & 25.13 —— 寻找“完美的采样点”
这两张图是在教我们怎么“偷懒”。
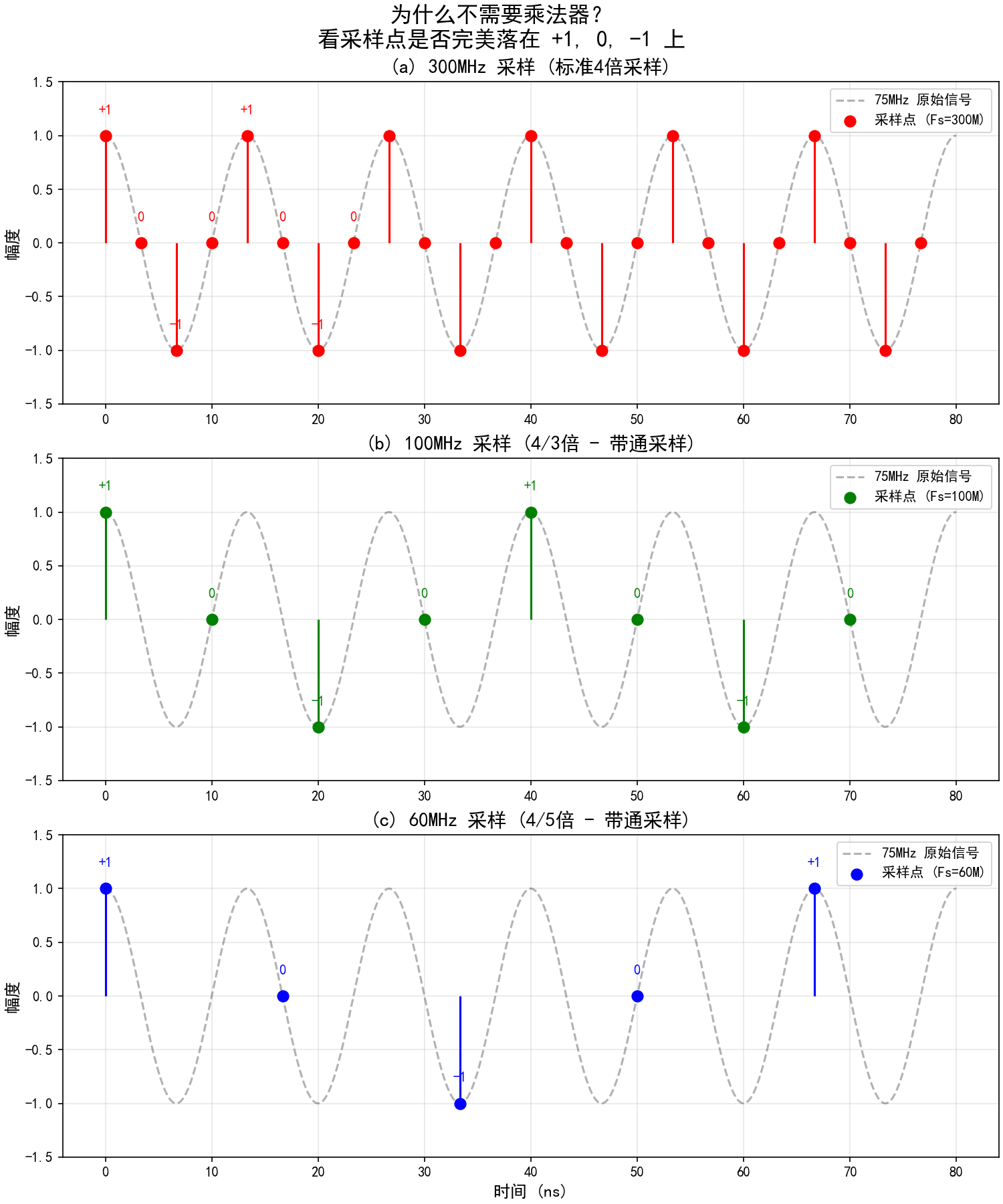
1. 笨办法但很完美(图 25.12)

2. 聪明的偷懒(图 25.13)


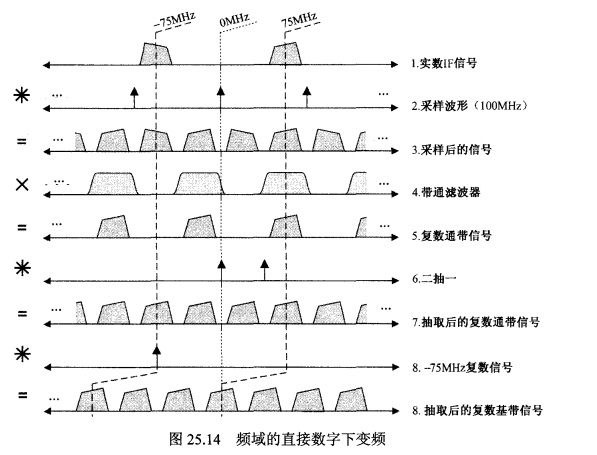
第二步:图 25.14 —— 频域里的“乾坤大挪移”
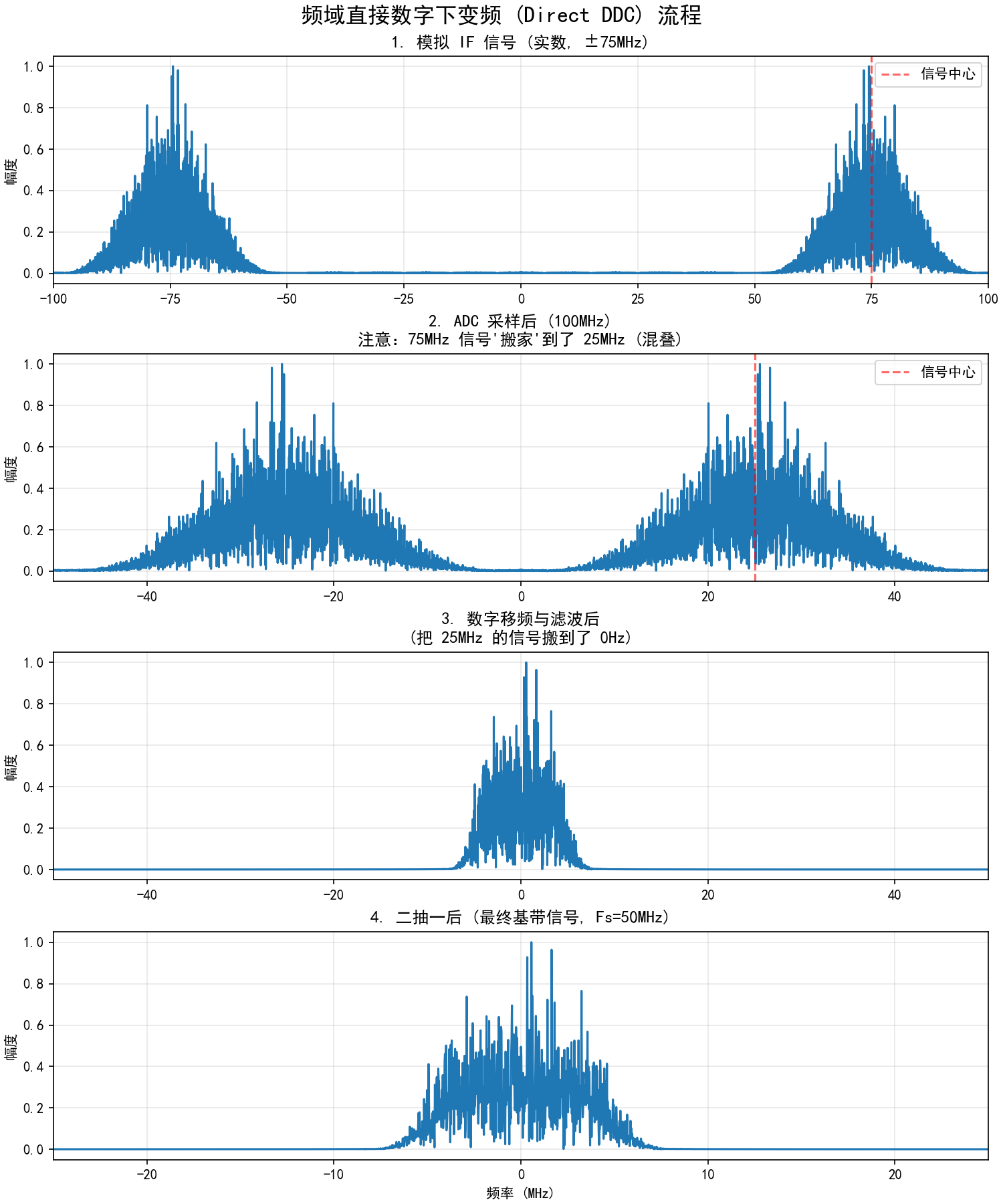
这张图解释了在上述的“聪明采样”下,信号在频率轴上发生了什么。这叫 直接数字下变频 (Direct DDC)。

第三步:文字图片 (图 25.15/16 的文字解释) —— 极致的省钱技巧
这部分文字主要解释了为什么图 25.14 第 4 行那个带通滤波器特别好做。
文中提到:“除中心以外的所有奇数号系数都为零”。
这是什么意思?

总结:这部分内容的“核心套路”
这几页书其实就在教你如何设计一个**“极其高效、极低成本”**的雷达或通信接收机:
-
不蛮干: 不用超高速 ADC 去硬采 75MHz,而是用 100MHz 或 60MHz 去“智取”(带通采样)。
-
利用巧合: 让采样点刚好落在波峰波谷,把乘法运算变成简单的开关切换。
-
利用混叠: 不去对抗混叠,而是利用混叠把高频信号“免费”搬运到低频处理。
-
精简算法: 使用系数有一半是 0 的特殊滤波器,让计算量再减半。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import firwin, lfilter, freqz
# =================配置区域=================
# 自动选择中文字体,确保中文能正常显示
import platform
system_name = platform.system()
if system_name == "Windows":
plt.rcParams['font.sans-serif'] = ['SimHei']
elif system_name == "Darwin": # Mac
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
else: # Linux 等
plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei']
plt.rcParams['axes.unicode_minus'] = False
print("🚀 === 直接数字下变频 (Direct DDC) 深度仿真开始 ===\n")
# ================= 第一部分:时域采样原理 (复刻图 25.12/25.13) =================
# 目标:展示不同采样率下,采样点是否能落在波峰/波谷/零点上
def plot_time_sampling():
f_if = 75e6 # 中频信号 75 MHz
period_if = 1 / f_if
# 模拟连续信号 (为了画出光滑的余弦波)
t_analog = np.linspace(0, 6 * period_if, 1000)
sig_analog = np.cos(2 * np.pi * f_if * t_analog) # 也就是 I路波形
fig, axes = plt.subplots(3, 1, figsize=(10, 12), constrained_layout=True)
# 定义三种采样率
# 定义三种采样率
# 修改:颜色改为单字母代码 ('r', 'g', 'b') 以兼容 markerfmt 格式
scenarios = [
{"fs": 300e6, "title": "(a) 300MHz 采样 (标准4倍采样)", "color": "r"}, # red -> r
{"fs": 100e6, "title": "(b) 100MHz 采样 (4/3倍 - 带通采样)", "color": "g"}, # green -> g
{"fs": 60e6, "title": "(c) 60MHz 采样 (4/5倍 - 带通采样)", "color": "b"} # blue -> b
]
for i, scen in enumerate(scenarios):
fs = scen["fs"]
# 计算采样点时间
# 我们取足够多的点来覆盖模拟时间段
ts = np.arange(0, t_analog[-1], 1 / fs)
# 计算这些时间点上的信号值
samples = np.cos(2 * np.pi * f_if * ts)
ax = axes[i]
# 画背景的模拟波形
ax.plot(t_analog * 1e9, sig_analog, 'k--', alpha=0.3, label='75MHz 原始信号')
# 画采样点
ax.scatter(ts * 1e9, samples, color=scen["color"], s=60, zorder=5, label=f'采样点 (Fs={fs / 1e6:.0f}M)')
ax.stem(ts * 1e9, samples, linefmt=scen["color"], markerfmt=scen["color"] + 'o', basefmt=" ")
# 装饰
ax.set_title(scen["title"], fontsize=14, fontweight='bold')
ax.set_ylabel("幅度", fontsize=12)
ax.set_ylim(-1.5, 1.5)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper right')
# 标注特殊序列
# 我们检查前几个点,看看是不是 1, 0, -1, 0
txt_y = 1.2
for j, val in enumerate(samples[:8]): # 标注前8个点
# 判断接近整数的值
if np.isclose(val, 1, atol=0.1):
lbl = "+1"
elif np.isclose(val, -1, atol=0.1):
lbl = "-1"
elif np.isclose(val, 0, atol=0.1):
lbl = "0"
else:
lbl = f"{val:.1f}"
ax.text(ts[j] * 1e9, val + 0.2, lbl, ha='center', fontsize=10, color=scen["color"], fontweight='bold')
axes[2].set_xlabel("时间 (ns)", fontsize=12)
plt.suptitle("为什么不需要乘法器?\n看采样点是否完美落在 +1, 0, -1 上", fontsize=16)
save_path = "DDC_Time_Domain.png"
plt.savefig(save_path, dpi=150)
print(f"[图1保存成功] {save_path} - 展示了时域上的'完美采样点'")
# ================= 第二部分:频域处理流程 (复刻图 25.14) =================
# 目标:展示 75MHz 信号如何通过 100MHz 采样和滤波变成基带
def plot_freq_process():
# 参数设置
fs_analog = 1000e6 # 模拟域
fs_adc = 100e6 # ADC 采样率
f_sig = 75e6 # 信号中心频率
bw = 10e6 # 信号带宽
duration = 50e-6 # 仿真时长
t = np.arange(0, duration, 1 / fs_analog)
# 1. 生成带通信号 (75MHz)
np.random.seed(0)
noise = np.random.randn(len(t))
b_bp = firwin(101, [f_sig - bw / 2, f_sig + bw / 2], fs=fs_analog, pass_zero=False)
sig_analog = lfilter(b_bp, 1, noise)
# 2. ADC 采样 (100MHz)
decim = int(fs_analog / fs_adc)
sig_adc = sig_analog[::decim] # 只有实数部分!
# 3. 构造复数带通信号 (模仿图25.14第4-5行)
# 在 100MHz 采样下,75MHz 混叠到 -25MHz (和 +25MHz,因为是实数)
# 我们用一个带通滤波器保留 +25MHz 的部分,滤掉 -25MHz 的部分
# 这一步把实数变成了复数 (Hilbert 变换也是类似原理)
# 设计一个复数带通滤波器 (只通正频率 25MHz)
# 这里的 25MHz 对应 normalized freq = 25/(100/2) = 0.5
# 为了演示简单,我们直接用移频法来模拟这个"提取正频率"的过程
# 实际上是用 Hilbert 变换或者复数滤波器
# 为了严格对应文中流程:先带通滤波(25MHz),再移频。
# 在数字域,混叠后的中心频率是 25MHz。
t_adc = np.arange(0, duration, 1 / fs_adc)
# 方法:数字混频把 +25MHz 搬到 0Hz
# 乘以 exp(-j * 2pi * 25M * t)
# 文中第8行说乘以 -75MHz,其实 -75 和 +25 在 100M 采样下是一回事 (差100M)
# 我们这里用 -25MHz 来移频,更直观
nco = np.exp(-1j * 2 * np.pi * 25e6 * t_adc)
sig_baseband = sig_adc * nco
# 4. 低通滤波 (滤除倍频分量)
b_lp = firwin(61, 5e6, fs=fs_adc)
sig_filtered = lfilter(b_lp, 1, sig_baseband)
# 5. 二抽一 (100M -> 50M)
sig_final = sig_filtered[::2]
fs_final = 50e6
# === 绘图 ===
fig, axes = plt.subplots(4, 1, figsize=(10, 12), constrained_layout=True)
# 辅助绘图函数
def plot_spec(ax, sig, fs, title, center_mark=None, xlim=100):
n = len(sig)
f = np.fft.fftshift(np.fft.fftfreq(n, 1 / fs)) / 1e6 # MHz
mag = np.fft.fftshift(np.abs(np.fft.fft(sig)))
mag = mag / np.max(mag)
ax.plot(f, mag, color='tab:blue')
ax.set_title(title, fontsize=12, fontweight='bold')
ax.set_ylabel("幅度")
ax.set_xlim(-xlim, xlim)
ax.grid(True, alpha=0.3)
if center_mark:
ax.axvline(center_mark, color='red', linestyle='--', alpha=0.6, label='信号中心')
ax.legend()
# 图1: 原始模拟信号
plot_spec(axes[0], sig_analog, fs_analog, "1. 模拟 IF 信号 (实数, ±75MHz)", center_mark=75)
# 图2: ADC采样后
# 解释:75MHz 信号在 100MHz 采样下,混叠频率 = |75 - 100| = 25MHz
plot_spec(axes[1], sig_adc, fs_adc, "2. ADC 采样后 (100MHz)\n注意:75MHz 信号'搬家'到了 25MHz (混叠)",
center_mark=25, xlim=50)
# 图3: 混频+滤波后 (变成复数基带)
plot_spec(axes[2], sig_filtered, fs_adc, "3. 数字移频与滤波后\n(把 25MHz 的信号搬到了 0Hz)", center_mark=0, xlim=50)
# 图4: 抽取后
plot_spec(axes[3], sig_final, fs_final, "4. 二抽一后 (最终基带信号, Fs=50MHz)", center_mark=0, xlim=25)
axes[3].set_xlabel("频率 (MHz)")
plt.suptitle("频域直接数字下变频 (Direct DDC) 流程", fontsize=16)
save_path = "DDC_Freq_Domain.png"
plt.savefig(save_path, dpi=150)
print(f"[图2保存成功] {save_path} - 展示了利用混叠进行搬移的过程")
if __name__ == "__main__":
plot_time_sampling()
plot_freq_process()
print("\n✅ 所有仿真完成!请查看生成的 .png 图片。")






















 241
241

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








