ADC的有效位数（ENOB）、信噪比（SNR）和无杂散动态范围（SFDR）——详细分析

这一部分（图25.20及其相关文本）是继续讨论ADC（模数转换器）实际性能的章节，主要焦点是有效位数（ENOB）、**信噪比（SNR）与输入频率的关系，以及无杂散动态范围（SFDR）**的概念。这些是评估ADC在真实应用中性能的关键指标，尤其在高频信号下。既然你的信号基础不太好，我会从最基础的概念开始，一步步解释，包括每个术语的含义、为什么会出现这些现象、相关公式，以及图25.20的分析。最后，我会用一些视觉图例来辅助理解。

1. 基础回顾：ADC的理想 vs 实际性能

• 理想ADC：一个n位ADC的理论SNR约为 6.02n + 1.76 dB（这是量化噪声限定的）。例如，12位ADC的理想SNR ≈ 74 dB。
• 实际ADC：由于各种噪声和失真（如热噪声、抖动、非线性失真），实际SNR会低于理想值。高频信号时，这些问题更严重，导致ADC的“有效性能”下降。
• 这部分文本强调：ADC的输入频率必须远低于其3dB截止频率（带宽上限），否则SNR会急剧下降。图25.20就是展示抖动如何限制SNR的典型例子。

2. 有效位数（ENOB）——ADC的“真实位数”

• 什么是ENOB？ ENOB（Effective Number of Bits）是衡量ADC实际分辨率的指标。它回答：“这个ADC在实际条件下，相当于一个理想的几位ADC？” 例如，一个标称12位ADC，如果实际ENOB=10位，意味着它的噪声和失真让它只相当于理想10位ADC的性能。
• 为什么需要ENOB？ 因为实际ADC有多种噪声源（如抖动、热噪声、非线性），这些会“吃掉”部分分辨率。文本中提到：由于ADC内部的噪声源（如抖动），实际SNR低于理想，导致ENOB < 标称位数。
  • 低频信号：ENOB接近标称位数（量化噪声主导）。
  • 高频信号：抖动等噪声主导，ENOB下降明显。
• ENOB的计算公式（文本中隐含，标准公式）：
• 
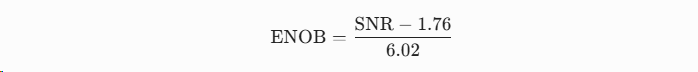
  • 这里SNR是实际测量的dB值。
  • 为什么是这个公式？因为理想n位ADC的SNR = 6.02n + 1.76 dB，反推n（即ENOB）就是这个。
  • 示例：如果实际SNR=68 dB，则ENOB ≈ (68 - 1.76)/6.02 ≈ 11位（标称12位ADC损失了1位）。 文本中说“ENOB (=SNR/6dB)”，这是近似（忽略1.76 dB，因为它小），实际精确公式如上。
• 文本中的关键点： ENOB是小信号时的指标（信号幅度小，噪声主导）。对于大信号，非线性失真更重要，这时用SFDR评估。

3. 无杂散动态范围（SFDR）——衡量ADC的线性度

• 什么是SFDR？ SFDR（Spurious-Free Dynamic Range）是ADC的动态性能指标，定义为：输入信号功率 与 最大杂散（spurious）信号功率 的比值（dB）。
  • 杂散信号：ADC输出中不应出现的频率成分（如谐波失真、互调失真），不是噪声，而是失真产物。
  • 示例：输入一个纯正弦波（单频f），理想输出只有f，但实际输出有2f、3f等谐波，这些就是杂散。 SFDR越高，说明ADC线性度越好，能处理更大动态范围的信号而不产生明显失真。
• SFDR vs SNR：
  • SNR关注总噪声（随机噪声，如抖动、热噪声）。
  • SFDR关注特定杂散（确定性失真）。
  • 文本中强调：典型ADC的SFDR > SNR（因为杂散通常比总噪声小）。例如，SNR=70 dB，SFDR可能=80 dB。
  • 但在高频下，抖动会让SNR下降更快，而SFDR可能受非线性影响。
  • 为什么重要？在通信、雷达等应用中，杂散会干扰其他信号通道，所以SFDR是关键规格。
• 测量SFDR： 通常输入满幅度单频信号，观察FFT谱，找最大杂散峰值。
• 文本中的关键点：
  • ADC的数据手册中会给出SFDR vs 输入频率的图。
  • SFDR比SNR高，不等于说可以用SFDR代替SNR设计。
  • 如果前面提到过，通过滤波或校准可以改善SFDR。
  • 在设计中，要查看厂家数据手册；实际测试时，用比较采样技术测量抖动规模。

4. 图25.20的详细分析：抖动对SNR/ENOB的影响

• 图的描述：
  • X轴：输入频率（MHz），从1到100 MHz。
  • Y轴左侧：SNR (dB)，从0到120 dB。
  • Y轴右侧：ENOB（位），从4到14位（因为ENOB ≈ SNR/6 dB）。
  • 多条曲线：对应不同RMS抖动水平（t_j），如0.5ps、1ps、2ps、10ps、50ps、250ps、1000ps。
  • 趋势：所有曲线都随频率增加而下降（斜率≈-20 dB/十倍频）。
• 为什么这样？（回顾抖动公式） 从上一节，抖动限定的SNR：
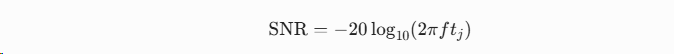
  • f（频率）增加，SNR线性下降（对数轴上呈直线）。
  • t_j（抖动）越大，曲线越低（SNR越差）。
  • 示例：对于t_j=1ps，f=10 MHz时SNR≈100 dB（ENOB≈16位）；f=100 MHz时SNR≈80 dB（ENOB≈13位）。
  • 实际中，低抖动（如<1ps）对高频ADC（如GHz采样）至关重要。
• 文本与图的联系：
  • 图展示不同抖动下的SNR下降曲线，证明高频时抖动是主导因素。
  • 结合ENOB：右轴直接显示ENOB损失（例如，抖动大时，高频ENOB可能降到6-8位）。
  • 3dB截止：输入频率应<< ADC带宽，否则SNR进一步下降。

下面是一些类似图25.20的参考图像，展示抖动对SNR的影响（这些是网络搜索到的示例图，帮助可视化）：

5. 实际应用与总结

• 设计提示（从文本）：
  • 选择ADC时，看数据手册的SNR、ENOB、SFDR vs 频率图。
  • 减小抖动：用低抖动时钟、优化PCB、电源滤波。
  • 对于大信号：关注SFDR（失真）；小信号：关注SNR/ENOB（噪声）。
  • 如果ENOB不足，用过采样或多ADC并行提升（但增加复杂度）。
• 为什么这段重要？ 它解释了为什么高速ADC（如用于5G、雷达）的规格那么贵：抖动和失真限制了高频性能。理解这些，能帮你避免设计陷阱。

代码实现

import numpy as np
import matplotlib.pyplot as plt

# 参数设置（与书中的图25.20一致）
frequencies = np.logspace(0, 2, 500)  # 1 MHz 到 100 MHz（对数轴）
frequencies = frequencies * 1e6  # 转换为 Hz

# 不同的 RMS 抖动值（单位：秒），对应书中的曲线
jitter_values_ps = [0.5, 1, 2, 10, 50, 250, 1000]  # ps
jitter_values_s = np.array(jitter_values_ps) * 1e-12  # 转换为秒

# 计算抖动限制下的 SNR（dB）
# SNR = -20 * log10(2 * π * f * t_j)
snr_db = []
for tj in jitter_values_s:
    snr = -20 * np.log10(2 * np.pi * frequencies * tj)
    snr_db.append(snr)

snr_db = np.array(snr_db)

# 计算对应的 ENOB（有效位数）
# ENOB = (SNR - 1.76) / 6.02   （精确公式）
# 书上用近似 ENOB ≈ SNR / 6
enob_precise = (snr_db - 1.76) / 6.02
enob_approx = snr_db / 6.02  # 书上常用近似值（略高一点）

# 绘图
plt.figure(figsize=(10, 7))

# 主坐标轴：SNR (dB)
for i, tj_ps in enumerate(jitter_values_ps):
    plt.plot(frequencies / 1e6, snr_db[i], label=f't_j = {tj_ps} ps', linewidth=2)

plt.xlabel('输入信号频率 (MHz)', fontsize=12)
plt.ylabel('SNR (dB)', fontsize=12)
plt.xscale('log')
plt.grid(True, which="both", ls="--", linewidth=0.5)
plt.title('不同时钟抖动下的 ADC 信噪比 SNR 与输入频率的关系', fontsize=14)
plt.legend()
plt.xlim(1, 100)
plt.ylim(0, 120)

# 副坐标轴：ENOB（位数）
ax2 = plt.twinx()
# 这里用近似值画 ENOB（与书上右轴一致）
for i, tj_ps in enumerate(jitter_values_ps):
    ax2.plot(frequencies / 1e6, snr_db[i] / 6.02, linewidth=2)  # 不显示第二次，避免图例重复

ax2.set_ylabel('ENOB (bits)', fontsize=12)
ax2.set_ylim(0, 120 / 6.02)
ax2.set_yticks(np.arange(4, 15, 2))

plt.tight_layout()
plt.show()