第一步:理解问题——我们要找什么?
我们想知道:一个雷达发射信号后,从一个目标反射回来的信号,在雷达接收机处有多强?

第二步:发射端——功率是如何辐射出去的?
-
理想点源(各向同性天线):

-
实际天线(有方向性):

至此,我们得到了照射到目标上的功率密度。
第三步:目标——目标如何“反射”信号?

第四步:回波传播——信号如何返回雷达?

至此,我们得到了到达雷达天线口面处的回波功率密度。
第五步:接收端——雷达如何“收集”回波?
雷达不能直接利用功率密度,它需要一个接收天线来收集这部分能量。

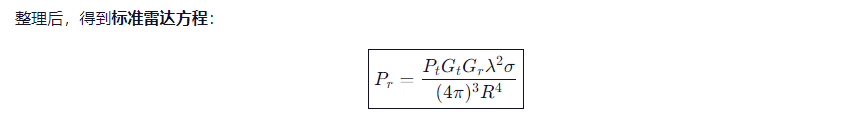
第六步:特殊情况——单基地雷达
在绝大多数雷达系统中,发射和接收使用的是同一个天线(称为单基地雷达)。这意味着:
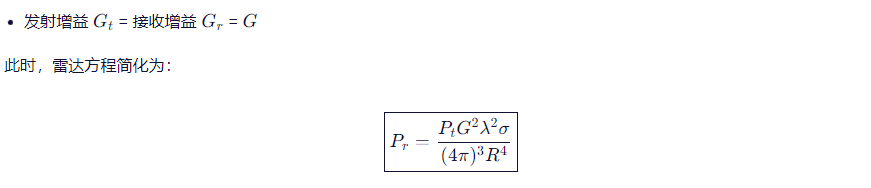
这个形式就是我们在《雷达手册》第1.4节开头看到的式 (1.2) 的核心。
总结与关键点

通过以上六步,我们从最基本的物理图像出发,完整地推导出了雷达方程。初学者可以按照这个逻辑,自己在纸上一步步重现整个过程。
Python实现
import numpy as np
import matplotlib.pyplot as plt
# ==============================
# 配置:自动处理中文字体
# ==============================
import matplotlib
zh_fonts = ['SimHei', 'Microsoft YaHei', 'STSong', 'PingFang SC', 'Noto Sans CJK SC']
found_font = None
for font in zh_fonts:
if font in [f.name for f in matplotlib.font_manager.fontManager.ttflist]:
found_font = font
break
if found_font:
plt.rcParams['font.sans-serif'] = [found_font]
plt.rcParams['axes.unicode_minus'] = False
USE_CHINESE = True
else:
USE_CHINESE = False
print("⚠️ 未检测到中文字体,界面将使用英文")
# ==============================
# 物理常数
# ==============================
c = 3e8 # 光速 (m/s)
k_B = 1.380649e-23 # 玻尔兹曼常数 (J/K)
T0 = 290 # 标准室温 (K)
# ==============================
# 雷达方程核心函数
# ==============================
def compute_radar_performance(Pt, f0, G_dB, sigma, B, F_dB, L_dB, R):
"""
计算雷达性能:SNR(dB) 和 接收功率 Pr(W)
返回:
SNR_dB: 信噪比 (dB)
Pr: 接收功率 (W)
N: 噪声功率 (W)
"""
wavelength = c / f0
G = 10**(G_dB / 10) # dB -> 线性
F = 10**(F_dB / 10)
L = 10**(L_dB / 10)
# --- 接收功率 Pr (线性域) ---
Pr = (Pt * G**2 * wavelength**2 * sigma) / ((4 * np.pi)**3 * R**4 * L)
# --- 噪声功率 N = kTB*F ---
N = k_B * T0 * B * F
# --- 信噪比 SNR (dB) ---
SNR_dB = 10 * np.log10(Pr / N)
return SNR_dB, Pr, N
# ==============================
# 主程序
# ==============================
if __name__ == "__main__":
# ------------------------------
# 雷达参数设置(可修改!)
# ------------------------------
Pt = 150 # 峰值功率 [W]
f0 = 10e9 # 载频 [Hz] → X波段
G_dB = 30 # 天线增益 [dB]
sigma_list = [0.01, 1, 5] # RCS [m²]: 小鸟/无人机、汽车、战斗机
B = 20e6 # 带宽 [Hz]
F_dB = 3 # 噪声系数 [dB]
L_dB = 6 # 系统损耗 [dB]
R_min, R_max = 2000, 10000 # 距离范围 [m]
R = np.linspace(R_min, R_max, 500)
# ------------------------------
# 计算所有曲线
# ------------------------------
results = {}
for sigma in sigma_list:
SNR, Pr, N = compute_radar_performance(Pt, f0, G_dB, sigma, B, F_dB, L_dB, R)
results[sigma] = {'SNR': SNR, 'Pr': Pr}
noise_power = k_B * T0 * B * (10**(F_dB/10)) # 固定噪声功率
# ------------------------------
# 找到 SNR=0 dB 的距离(Pr = N)
# ------------------------------
R_SNR0 = {}
for sigma in sigma_list:
snr = results[sigma]['SNR']
# 找到最接近 0 dB 的点
idx = np.argmin(np.abs(snr))
R_SNR0[sigma] = R[idx]
# ------------------------------
# 绘图
# ------------------------------
fig, axs = plt.subplots(1, 2, figsize=(14, 6))
# --- 左图:SNR vs 距离 ---
colors = ['tab:red', 'tab:blue', 'tab:purple']
for i, sigma in enumerate(sigma_list):
axs[0].plot(R/1000, results[sigma]['SNR'], color=colors[i],
label=f'RCS = {sigma} m²')
# 标注 SNR=0 点
axs[0].scatter(R_SNR0[sigma]/1000, 0, color=colors[i], s=50, zorder=5)
axs[0].axhline(0, color='black', linestyle='--', linewidth=0.8, alpha=0.7)
axs[0].set_xlabel('距离 (km)' if USE_CHINESE else 'Range (km)')
axs[0].set_ylabel('信噪比 SNR (dB)' if USE_CHINESE else 'SNR (dB)')
axs[0].set_title('SNR 随距离变化' if USE_CHINESE else 'SNR vs Range')
axs[0].grid(True, linestyle='--', alpha=0.6)
axs[0].legend()
# --- 右图:接收功率 Pr vs 距离(对数坐标)---
for i, sigma in enumerate(sigma_list):
axs[1].semilogy(R/1000, results[sigma]['Pr'], color=colors[i],
label=f'RCS = {sigma} m²')
# 标注 Pr = N 的点
axs[1].scatter(R_SNR0[sigma]/1000, noise_power, color=colors[i], s=50, zorder=5)
axs[1].axhline(noise_power, color='black', linestyle='--', linewidth=0.8, alpha=0.7,
label='噪声功率 $N = kTB F$')
axs[1].set_xlabel('距离 (km)' if USE_CHINESE else 'Range (km)')
axs[1].set_ylabel('接收功率 $P_r$ (W)' if USE_CHINESE else 'Received Power $P_r$ (W)')
axs[1].set_title('接收功率 vs 距离' if USE_CHINESE else 'Received Power vs Range')
axs[1].grid(True, which="both", linestyle='--', alpha=0.6)
axs[1].legend()
plt.tight_layout()
plt.show()
# ------------------------------
# 打印详细结果摘要
# ------------------------------
print("\n" + "="*60)
if USE_CHINESE:
print("📡 雷达方程分析报告")
else:
print("📡 Radar Equation Analysis Report")
print("="*60)
print(f"发射功率 Pt : {Pt} W")
print(f"工作频率 f0 : {f0/1e9:.1f} GHz (λ = {c/f0:.3f} m)")
print(f"天线增益 G : {G_dB} dB")
print(f"信号带宽 B : {B/1e6:.1f} MHz")
print(f"噪声系数 F : {F_dB} dB")
print(f"系统损耗 L : {L_dB} dB")
print(f"噪声功率 N : {noise_power:.3e} W ({10*np.log10(noise_power):.1f} dBm)")
print("-"*60)
for sigma in sigma_list:
r0 = R_SNR0[sigma] / 1000 # km
if USE_CHINESE:
print(f"• RCS = {sigma:>5} m² 时,SNR=0 dB 的距离 ≈ {r0:.2f} km")
else:
print(f"• At RCS = {sigma:>5} m², range where SNR=0 dB ≈ {r0:.2f} km")
print("\n💡 说明:")
if USE_CHINESE:
print(" - SNR > 0 dB 表示信号强于噪声,目标可能被检测到")
print(" - 接收功率随距离呈 1/R⁴ 衰减(图中为对数坐标下的直线)")
print(" - 更大的 RCS 或更高的增益可显著提升探测距离")
else:
print(" - SNR > 0 dB means signal is stronger than noise (detectable)")
print(" - Received power decays as 1/R⁴ (straight line on log-log plot)")
print(" - Larger RCS or higher gain significantly extends detection range")
运行结果
============================================================
📡 雷达方程分析报告
============================================================
发射功率 Pt : 150 W
工作频率 f0 : 10.0 GHz (λ = 0.030 m)
天线增益 G : 30 dB
信号带宽 B : 20.0 MHz
噪声系数 F : 3 dB
系统损耗 L : 6 dB
噪声功率 N : 1.598e-13 W (-128.0 dBm)
------------------------------------------------------------
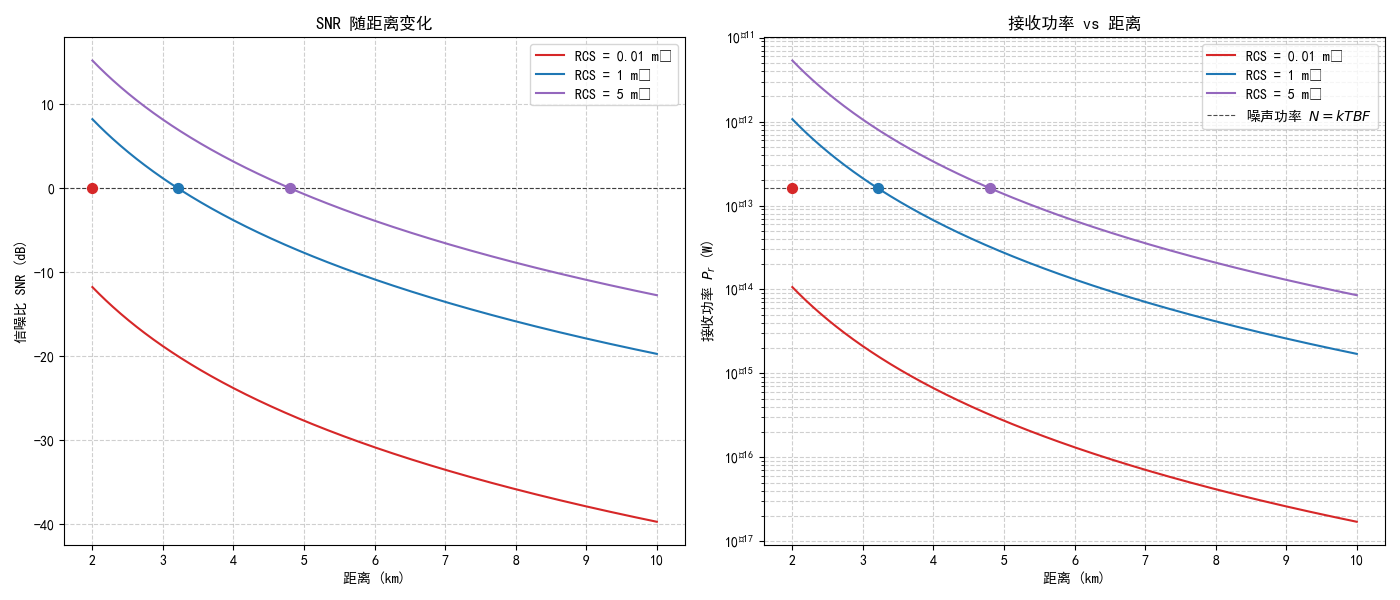
• RCS = 0.01 m² 时,SNR=0 dB 的距离 ≈ 2.00 km
• RCS = 1 m² 时,SNR=0 dB 的距离 ≈ 3.22 km
• RCS = 5 m² 时,SNR=0 dB 的距离 ≈ 4.81 km
💡 说明:
- SNR > 0 dB 表示信号强于噪声,目标可能被检测到
- 接收功率随距离呈 1/R⁴ 衰减(图中为对数坐标下的直线)
- 更大的 RCS 或更高的增益可显著提升探测距离






















 1808
1808

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








