数据结构_02_线性结构

原创 于 2019-06-26 08:31:04 发布 · 341 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文详细介绍了数据结构中的线性结构，包括线性表、栈、队列和串的相关概念、存储结构和操作。重点讲解了顺序表与链表的比较，以及线性表的顺序存储和链式存储实现。同时，提到了栈和队列的性质、操作及应用，如中缀表达式转后缀表达式。此外，还讨论了串的模式匹配算法，如简单的匹配和KMP算法。

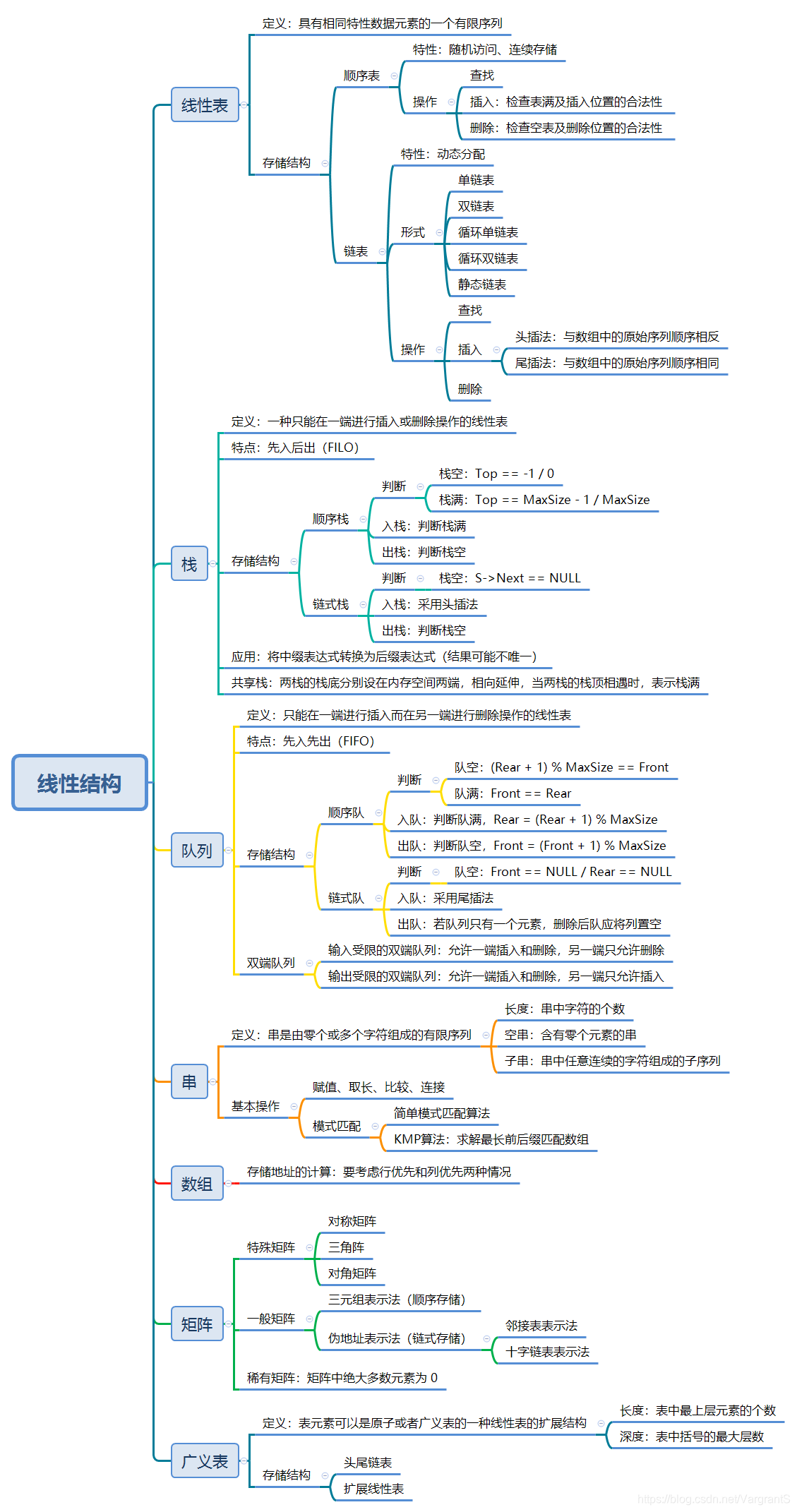
在这里插入图片描述

一、线性表

1. 相关概念
  1. 定义：线性表是具有相同特性数据元素的一个有限序列。序列中所含元素的个数叫做线性表的长度，用 n n n 表示。当 n = 0 n=0 n=0 时，即表示该表为空表。
  2. 表头、表尾、前驱、后继；
  3. 存储结构：顺序存储结构（顺序表）、链式存储结构（链表）；
  4. 链表的形式：单链表、双链表、循环单链表、循环双链表、静态链表（结构体数组）；
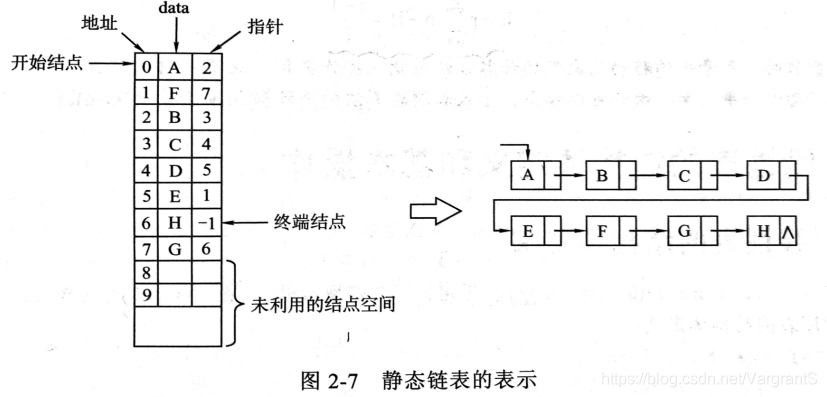
    在这里插入图片描述
    注意：静态链表中的指针是指存储数组下标的整形变量；
2. 顺序表和链表的比较
  • 顺序表：具有随机访问特性，要求占用连续的存储空间（静态分配）；
  • 链表：不支持随机访问，存储空间利用率较顺序表稍低，支持动态分配；
  1. 基于空间的比较
    1）存储分配的方式：
    顺序表的存储空间是一次性分配的，链表的存储空间是多次分配的；
    2）存储密度（ 存储密度 = 站点值域所占的存储量 / 站点结构所占的存储总量）
    顺序表的存储密度 = 1，链表的存储密度<1（结点中有指针域）；
  2. 基于时间的比较
    1）存取方式：
    顺序表可以随机存取，也可以顺序存取；链表只能顺序存取；
    【所谓顺序存取，以读取为例，要读取某个元素必须遍历其之前的所有元素才能找到它并读取之】
    2）插入/删除时移动元素的个数：
    顺序表平均需要移动近一半元素；链表不需要移动元素，只需要修改指针。
    具有 n n n 个元素的顺序表，插入一个元素所进行的平均移动个数为：
    E = p ∑ i = 1 n ( n − i ) = n − 1 2 E=p\sum_{i=1}^n(n-i)=\frac{n-1}{2} E=pi=1∑n​(n−i)=2n−1​
3. 顺序表
  1. 结构体定义：
// 链表--顺序存储结构
typedef int ElementType;
typedef int Position;

#define MAXSIZE 10000
typedef struct LNode *List;
struct LNode {
	ElementType Data[MAXSIZE];
	Position Last;	// 也可表示链表的长度	
};
  1. 基本操作
/* 初始化 */
List MakeEmpty()
{
	List L;
	L = (List)malloc(sizeof(struct LNode));
	L->Last = -1;	// = 0，视情况而定
	return L;
}

/* 查找 */
#define ERROR -1
Position Find(List L, ElementType X)
{
	Position i = 0;
	while (i <= L->Last && L->Data[i] != X)
		i++;
	if (i > L->Last)  return ERROR; /* 如果没找到，返回错误信息 */
	else  return i;  /* 找到后返回的是存储位置 */
}

/* 插入 */
bool Insert(List L, ElementType X, Position P)
{ /* 在L的指定位置P前插入一个新元素X */
	Position i;
	if (L->Last == MAXSIZE - 1) {
		/* 表空间已满，不能插入 */
		printf("表满");
		return false;
	}
	if (P<0 || P>L->Last + 1) { /* 检查插入位置的合法性 */
		printf("位置不合法");
		return false;
	}

	for (i = L->Last; i >= P; i--)
		L->Data[i + 1] = L->Data[i]; /* 将位置P及以后的元素顺序向后移动 */
	L->Data[P] = X;  /* 新元素插入 */
	L->Last++;       /* Last仍指向最后元素 */
	return true;
}

/* 删除 */
bool Delete(List L, Position P)
{ /* 从L中删除指定位置P的元素 */
	Position i;
	if (P<0 || P>L->Last) { /* 检查空表及删除位置的合法性 */
		printf("位置%d不存在元素", P);
		return false;
	}

	for (i = P + 1; i <= L->Last; i++)
		L->Data[i - 1] = L->Data[i]; /* 将位置P+1及以后的元素顺序向前移动 */
	L->Last--; /* Last仍指向最后元素 */
	return true;
}
4. 单链表（含头结点）
  1. 基本定义
// 链表 -- 链式存储
// 注意链表 是否包含头结点
typedef int ElementType;
typedef struct LNode *PtrToLNode;
struct LNode {
	ElementType Data;
	PtrToLNode Next;
//	PtrToLNode Prior;	// 双链表
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
  1. 基本操作
/* 建立链表 */
List CreatList(ElementType a[], int n)
{
	List L = (List)malloc(sizeof(LNode));
	L->Next = NULL;
	Position P,tmp;
	P = L;
	for(int i=0; i<n; i++){
		tmp = (Position)malloc(sizeof(LNode));
		tmp->Data = a[i];
		// 尾插法：与数组中的原始序列顺序相同
		P->Next = tmp;
		P = P-Next;
		/* 头插法：与数组中的原始序列顺序相反
		tmp->Next = L->Next;
		L->Next = tmp;
		*/
	}
	P->Next = NULL;
}

/* 查找 */
#define ERROR NULL
Position Find(List L, ElementType X)
{
	Position p = L; /* p指向L的第1个结点 */
	while (p && p->Data != X)
		p = p->Next;

	/* 下列语句可以用 return p; 替换 */
	if (p)
		return p;
	else
		return ERROR;
}

/* 带头结点的插入 */
bool Insert(List L, ElementType X, Position P)
{ /* 这里默认L有头结点 */
	Position tmp, pre;
	/* 查找P的前一个结点 */
	for (pre = L; pre&&pre->Next != P; pre = pre->Next);

	if (pre == NULL) { /* P所指的结点不在L中 */
		printf("插入位置参数错误\n");
		return false;
	}
	else { /* 找到了P的前一个结点pre */
		/* 在P前插入新结点 */
		tmp = (Position)malloc(sizeof(struct LNode)); /* 申请、填装结点 */
		tmp->Data = X;
		tmp->Next = P;
		pre->Next = tmp;
		return true;
	}
}

/* 带头结点的删除 */
bool Delete(List L, Position P)
{ /* 这里默认L有头结点 */
	Position tmp, pre;

	/* 查找P的前一个结点 */
	for (pre = L; pre&&pre->Next != P; pre = pre->Next);

	if (pre == NULL || P == NULL) { /* P所指的结点不在L中 */
		printf("删除位置参数错误\n");
		return false;
	}
	else { /* 找到了P的前一个结点pre */
		/* 将P位置的结点删除 */
		pre->Next = P->Next;
		free(P);
		return true;
	}
}

Ps：

  1. 关于双链表与循环链表，根据单链表进行类推即可，需要注意的是，双链表中判断 指针 p 走到表尾的条件是：
	p->Next == head
典型例题
  1. 数组循环左/右移
  2. 多项式的加法和乘法

二、栈

1. 相关概念
  1. 定义：栈是一种只能在一端进行插入或删除操作的线性表；
  2. 特点：先入后出（FILO）
  3. 存储结构：顺序栈、链式栈；
  4. 数学性质：当 n n n 个元素以某种顺序进栈，且可以在任意时刻出栈时，所获得的元素排列的数目 N N N 满足函数 C a t a l a n ( ) Catalan() Catalan() 的计算，即：
    N = 1 n + 1 C 2 n n N = \frac{1}{n+1}C^{n}_{2n} N=n+11​C2nn​
2. 顺序栈
  1. 结构体定义
// 栈 -- 顺序存储
typedef int ElementType;
typedef int Position;
struct SNode {
	ElementType *Data; /* 存储元素的数组 */
	Position Top;      /* 栈顶指针 */
	int MaxSize;       /* 堆栈最大容量 */
};
typedef struct SNode *Stack;
  1. 基本操作
Stack CreateStack(int MaxSize)
{
	Stack S = (Stack)malloc(sizeof(struct SNode));
	S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
	S->Top = -1;
	S->MaxSize = MaxSize;
	return S;
}

bool IsFull(Stack S)
{
	return (S->Top == S->MaxSize - 1);
}

bool Push(Stack S, ElementType X)
{ /* 将元素X压入堆栈S */
	if (IsFull(S)) {
		printf("堆栈满");
		return false;
	}
	else {
		S->Data[++(S->Top)] = X;
		return true;
	}
}

bool IsEmpty(Stack S)
{ /* 判断堆栈S是否为空，若是返回true；否则返回false */
	return (S->Top == -1);
}

#define ERROR -1
ElementType Pop(Stack S)
{ /* 删除并返回堆栈S的栈顶元素 */
	if (IsEmpty(S)) {
		printf("堆栈空");
		return ERROR; /* ERROR是ElementType的特殊值，标志错误 */
	}
	else
		return (S->Data[(S->Top)--]);
}
3. 链栈
// 栈 -- 链式存储
typedef int ElementType;
typedef struct SNode *PtrToSNode;
struct SNode {
	ElementType Data;
	PtrToSNode Next;
};
typedef PtrToSNode Stack;

Stack CreateStack()
{ /* 构建一个堆栈的头结点，返回该结点指针 */
	Stack S;
	S = (Stack)malloc(sizeof(struct SNode));
	S->Next = NULL;		// 始终指向栈顶
	return S;
}

bool IsEmpty(Stack S)
{ /* 判断堆栈S是否为空，若是返回true；否则返回false */
	return (S->Next == NULL);
}

bool Push(Stack S, ElementType X)
{ /* 将元素X压入堆栈S */
	PtrToSNode TmpCell;
	TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
	TmpCell->Data = X;
	TmpCell->Next = S->Next;	//采用头插法
	S->Next = TmpCell;
	return true;
}

#define ERROR -1
ElementType Pop(Stack S)
{ /* 删除并返回堆栈S的栈顶元素 */
	PtrToSNode FirstCell;
	ElementType TopElem;
	if (IsEmpty(S)) {
		printf("堆栈空");
		return ERROR;
	}
	else {
		FirstCell = S->Next;
		TopElem = FirstCell->Data;
		S->Next = FirstCell->Next;
		free(FirstCell);
		return TopElem;
	}
}
4. 相关应用
  1. 将中缀表达式转换为后缀表达式（结果不一定唯一）
5. 补充说明
  1. 共享栈：当两个栈共享一片连续的内存空间时，应将两栈的栈底分别设在这片内存空间的两端，而当两个栈的栈顶在栈空间的某一位置相遇时，则表示栈满。

三、队列

1. 相关概念
  1. 定义：只能在一端进行插入而在另一端进行删除操作的线性表；
  2. 特点：先入先出（FIFO）
  3. 存储结构：顺序队、链队；
2. 顺序队（循环队列）
  1. 结构体定义
// 队列 -- 顺序存储
typedef int ElementType;
typedef int Position;
struct QNode {
	ElementType *Data;     /* 存储元素的数组 */
	Position Front, Rear;  /* 队列的头、尾指针 */
	int MaxSize;           /* 队列最大容量 */
};
typedef struct QNode *Queue;
  1. 基本操作
Queue CreateQueue(int MaxSize)
{
	Queue Q = (Queue)malloc(sizeof(struct QNode));
	Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
	Q->Front = Q->Rear = 0;
	Q->MaxSize = MaxSize;
	return Q;
}

bool IsFull(Queue Q)
{	// 队空
	return ((Q->Rear + 1) % Q->MaxSize == Q->Front);
}

bool IsEmpty(Queue Q)
{	// 队满
	return (Q->Front == Q->Rear);
}

bool AddQ(Queue Q, ElementType X)
{
	if (IsFull(Q)) {
		printf("队列满");
		return false;
	}
	else {
		Q->Rear = (Q->Rear + 1) % Q->MaxSize;
		Q->Data[Q->Rear] = X;
		return true;
	}
}

#define ERROR -1
ElementType DeleteQ(Queue Q)
{
	if (IsEmpty(Q)) {
		printf("队列空");
		return ERROR;
	}
	else {
		Q->Front = (Q->Front + 1) % Q->MaxSize;
		return  Q->Data[Q->Front];
	}
}
3. 链队
  1. 结构体定义
// 队列 -- 链式存储
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node { /* 队列中的结点 */
	ElementType Data;
	PtrToNode Next;
};
typedef PtrToNode Position;

struct QNode {
	Position Front, Rear;  /* 队列的头、尾指针 */
	int MaxSize;           /* 队列最大容量 */
};
typedef struct QNode *Queue;
  1. 基本操作
bool IsEmpty(Queue Q)
{
	return (Q->Front == NULL);
}

bool AddQ(Queue Q, ElementType X)
{
	if (IsFull(Q)) {
		printf("队列满");
		return false;
	}
	else {
		PtrToNode TmpCell;
		TmpCell = (PtrToNode)malloc(sizeof(struct Node));
		TmpCell->Data = X;
		Q->Rear->Next = TmpCell;	//采用尾插法
		S->Rear = TmpCell;
	}
}

#define ERROR -1
ElementType DeleteQ(Queue Q)
{
	Position FrontCell;
	ElementType FrontElem;

	if (IsEmpty(Q)) {
		printf("队列空");
		return ERROR;
	}
	else {
		FrontCell = Q->Front;
		if (Q->Front == Q->Rear) /* 若队列只有一个元素 */
			Q->Front = Q->Rear = NULL; /* 删除后队列置为空 */
		else
			Q->Front = Q->Front->Next;
		FrontElem = FrontCell->Data;
		free(FrontCell);  /* 释放被删除结点空间  */
		return  FrontElem;
	}
}
5. 补充说明
  1. 双端队列：一种插入和删除在两端均可进行的线性表，可以将其看作栈底相连的两个栈，且栈顶向两端延伸。允许在一端进行插入和删除，另一端只允许删除的双端队列称为输入受限的双端队列；允许在一端进行插入和删除，另一端只允许插入的双端队列称为输出受限的双端队列；
    图自百度

四、串

1. 相关概念
  1. 串是由零个或多个字符组成的有限序列。串中字符的个数称为串的长度，含有零个元素的串叫做空串；
  2. 串中任意连续的字符组成的子序列称为该串的子串，包含子串的串称为主串，对于一个长度为 n n n 的字符串，其子串的个数为： n ( n + 1 ) 2 + 1 \frac{n(n+1)}{2}+1 2n(n+1)​+1；
  3. 对一个串中某子串的定位操作称为串的模式匹配，其中待定位的子串成为模式串；
2. 模式匹配算法
  1. 简单模式匹配算法： O ( n 2 ) O(n^2) O(n2)
int index(char* str, char* substr)
{
	int i = 0, j = 0, k = i;
	while(i <= str.length && j <= substr.length){
		if(str[i] == substr[j]){
			i++;j++;
		}
		else{
			j = 0;
			i = ++k;
		}
	}
	if(j >substr.length)
		return k;
	else
		return 0;
}
  1. KMP 算法： O ( n + m ) O(n+m) O(n+m)
typedef int Position;
#define NotFound -1

void BuildMatch(char *pattern, int *match)
{
	Position i, j;
	int m = strlen(pattern);
	match[0] = -1;

	for (j = 1; j < m; j++) {
		i = match[j - 1];
		while ((i >= 0) && (pattern[i + 1] != pattern[j]))
			i = match[i];
		if (pattern[i + 1] == pattern[j])
			match[j] = i + 1;
		else match[j] = -1;
	}
}

Position KMP(char *string, char *pattern)
{
	int n = strlen(string);
	int m = strlen(pattern);
	Position s, p, *match;

	if (n < m) return NotFound;
	match = (Position *)malloc(sizeof(Position) * m);
	BuildMatch(pattern, match);
	s = p = 0;
	while (s < n && p < m) {
		if (string[s] == pattern[p]) {
			s++; p++;
		}
		else if (p > 0) p = match[p - 1] + 1;
		else s++;
	}
	return (p == m) ? (s - m) : NotFound;
}

注意：在 KMP 算法中，由于主串不需要回溯，所以对于规模较大的外存中的模式匹配问题，可以分段进行，即先将部分内容读入内存，完成之后再写回外存，确保发生不匹配时不需要将之前写回外存的部分再次读入。减少了 I/O 操作，提高了效率。

五、数组、矩阵和广义表

1. 数组
  1. 对于数组的存储地址的计算，要考虑行优先和列优先两种情况；
2. 矩阵
  • 矩阵，一般采用二维数组表示；
  • 特殊矩阵（矩阵中相同元素的分布存在一定规律）和稀疏矩阵（矩阵中绝大多数元素为 0）；
2.1 特殊矩阵
  1. 对称矩阵：矩阵中的元素满足 a i , j = a j , i a_{i,j}=a_{j,i} ai,j​=aj,i​ ，对称矩阵在一维数组中的表示如下：
a 0 , 0 a_{0,0} a0,0​ a 0 , 0 a_{0,0} a0,0​… a n − 1 , 0 a_{n-1,0} an−1,0​ a n − 1 , 1 a_{n-1,1} an−1,1​… a n − 1 , n − 1 a_{n-1,n-1} an−1,n−1​
01… n × ( n − 1 ) 2 \frac{n\times(n-1)}2 2n×(n−1)​ n × ( n − 1 ) 2 + 1 \frac{n\times(n-1)}2+1 2n×(n−1)​+1… ( 1 + n ) × n 2 − 1 \frac{(1+n)\times n}2-1 2(1+n)×n​−1
  1. 三角阵：上三角阵（矩阵下三角（不包括对角线）元素全为 c c c）、下三角阵（矩阵上三角（不包括对角线）元素全为 c c c（ c c c 可以为 0 0 0 ）），其中下三角阵在一维数组中的表示为：
a 0 , 0 a_{0,0} a0,0​ a 0 , 0 a_{0,0} a0,0​… a n − 1 , 0 a_{n-1,0} an−1,0​ a n − 1 , 1 a_{n-1,1} an−1,1​… a n − 1 , n − 1 a_{n-1,n-1} an−1,n−1​c
01… n × ( n − 1 ) 2 \frac{n\times(n-1)}2 2n×(n−1)​ n × ( n − 1 ) 2 + 1 \frac{n\times(n-1)}2+1 2n×(n−1)​+1… ( 1 + n ) × n 2 − 1 \frac{(1+n)\times n}2-1 2(1+n)×n​−1 ( 1 + n ) × n 2 \frac{(1+n)\times n}2 2(1+n)×n​
  1. 对角矩阵：除主对角线以及其上下两条带状区域内的元素外，其余元素皆为 c c c（ c c c 可以为 0 0 0 ）
2.2 一般矩阵的表示方法
  1. 三元组表示法（顺序存储）：行优先
struct matrix{
	ElementType val;
	int i,j;
}
  1. 伪地址表示法（链式存储）：邻接表表示法、十字链表表示法
    在这里插入图片描述
3. 广义表
  1. 广义表：表元素可以是原子或者广义表的一种线性表的扩展结构，其中广义表的长度为表中最上层元素的个数，深度为表中括号的最大层数。当表非空时，第一个元素为表头，其余元素组成的表示广义表的表尾，举例：
    A = ( ) A=() A=() —— 空表
    B = ( d , e ) B=(d,e) B=(d,e) —— 长度为 2，深度为 1
    C = ( b , ( c , d ) ) C=(b,(c,d)) C=(b,(c,d)) —— 长度为 2，深度为 2
    D = ( B , C ) D=(B,C) D=(B,C) —— 长度为 2，深度为 3
  2. 头尾链表存储结构：原子结点（标记域、数据域）和广义表结点（标记域、头指针域、尾指针域），标记域用来区分当前结点是原子还是广义表，头指针域指向原子或广义表结点，尾指针域为空或者指向本层中的下一个广义表结点；
    在这里插入图片描述
  3. 扩展线性表存储结构：原子结点（标记域、数据域、尾指针域）和广义表结点（标记域、头指针域、尾指针域），类似于带头结点的单链表；
    在这里插入图片描述
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值