代码随想录算法训练营第 4 天 | 24. 两两交换链表中的节点、19. 删除链表的倒数第 N 个结点、面试题 02.07. 链表相交、142. 环形链表 II-优快云博客

24. 两两交换链表中的节点

重点：

cur 指向接下来要交换的两个节点的前一个节点
用 temp 和 temp1 两个临时变量保存第 1 和 3 号节点

易错点：
循环跳出条件为 cur.next != null && cur.next.next != null

在这里插入图片描述

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummyHead = new ListNode(0);
        dummyHead.next = head;
        ListNode cur = dummyHead;
        for (; cur.next != null && cur.next.next != null;) {
            ListNode temp = cur.next;
            ListNode temp1 = temp.next.next;
            cur.next = temp.next;
            cur.next.next = temp;
            temp.next = temp1;
            cur = temp;
        }
        return dummyHead.next;
    }
}

// TODO：难理解的递归

class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = head.next;
        head.next = swapPairs(newHead.next);
        newHead.next = head;
        return newHead;
    }
}

评论区的好的理解：

递归题目的要领，只需要分析一组数据，找出递归终止条件即可，后面的节点都看作一个整体（节点）。
比如，这个题目中 1，2，3，4 数据。我们分析 1 与 2 的交换过程。首先，找到终止条件，即当前节点为 null 或者节点的 next 为 null。
然后看 1 与 2，因为我们要断开 2 节点与后面节点的关系。所以需要一个节点暂存一下节点 2 即，ListNode newHead = head.next;。然后将 1 节点指向后面的节点，即 head.next = newHead.next，然后将 2 节点的 next 指向 1 节点。newHead.next = head; 我们返回 newHead 即可。因为，我们需要将这个过程重复执行，所以需要对 newHead.next 执行同样的操作，即 head.next = swapPairs (newHead.next);

19. 删除链表的倒数第 N 个结点

题目链接

难想到的点：
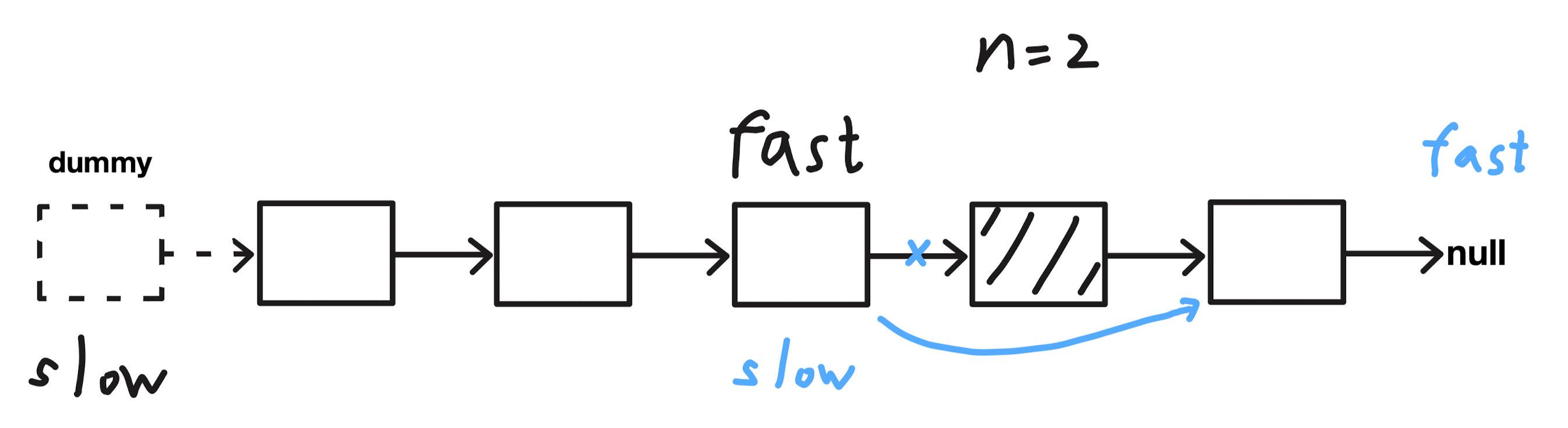
用快慢指针。让快指针先走 n 步，然后快慢指针再一起移动，这样当快指针走到 null 的时候，慢指针就停在了要删除的位置。

用快慢指针的好处：不用计算链表长度

当然，深究一下，因为慢指针需要停在要删除的节点的前一个节点。所以需要让上面的快指针先走 n + 1 步。

19. 删除链表的倒数第 N 个结点

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummyHead = new ListNode(0);
        dummyHead.next = head;
        ListNode slow = dummyHead, fast = dummyHead;

        // 让快指针先走 n + 1 步
        for (int i = 0; i <= n && fast != null; i++) {
            fast = fast.next;
        }
        
        // 快慢指针同时走
        for (; fast != null;) {
            slow = slow.next;
            fast = fast.next;
        }
        slow.next = slow.next.next;
        return dummyHead.next;
    }
}

面试题 02.07. 链表相交

题目链接

关键点：
两根链表不可能在某个结点相遇之后又分开或者相遇一段时间再分开，一旦相遇，就会一直在一起[浪漫]

因为是链表！！！链表都是单个指针，不可能有两个孩子（不是树）。一个结点确定那么后续的结点全部确定。所以一旦一个结点归两个链表共同拥有，那么它们后续的结点也完全一致！

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // 0 <= m, n <= 3 * 10^4
        int sizeA = getSize(headA);
        int sizeB = getSize(headB);

        // 计算两链表长度之差 n，将来让长的链表先移动 n 个单位
        int n = Math.abs(sizeA - sizeB);

        ListNode curA = headA, curB = headB;
        while (n-- > 0) {
            if (sizeA > sizeB) {
                curA = curA.next;
            } else {
                curB = curB.next;
            }
        }
        for (; curA != null;) {
            if (curA == curB) {
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
    }

    public int getSize(ListNode head) {
        int size = 0;
        for (; head != null; head = head.next) {
            size++;
        }
        return size;
    }
}

哈希集合法：
代码实现更加方便。但是空间复杂度是 O(n)，双指针法为 O(1)

神一样的方法：
链接

142. 环形链表 II

题目链接

其实是两个问题：

如何判断有环？
如果有环，在哪个结点开始入环？

第1 个问题是第 2 个问题的基础。

对于是否有环，只需设快慢指针，快指针每次移动 2，慢指针每次移动 1。如果快慢指针能相遇，则说明有环。

对于在哪个结点开始入环，只需分别在相遇点和链表头部设置一个指针，让它们同时移动（每次移动 1），相遇的地方就是开始入环的结点。

涉及到的数学证明：

为什么如果有环，快慢指针一定能相遇？
快指针比慢指针快 1，当慢指针进入环时，快指针相当于以 1 的速度在环里追慢指针，则一定能遇上
为什么一个从起点出发，一个从相遇点出发，当相遇时，相遇点就是入环点？

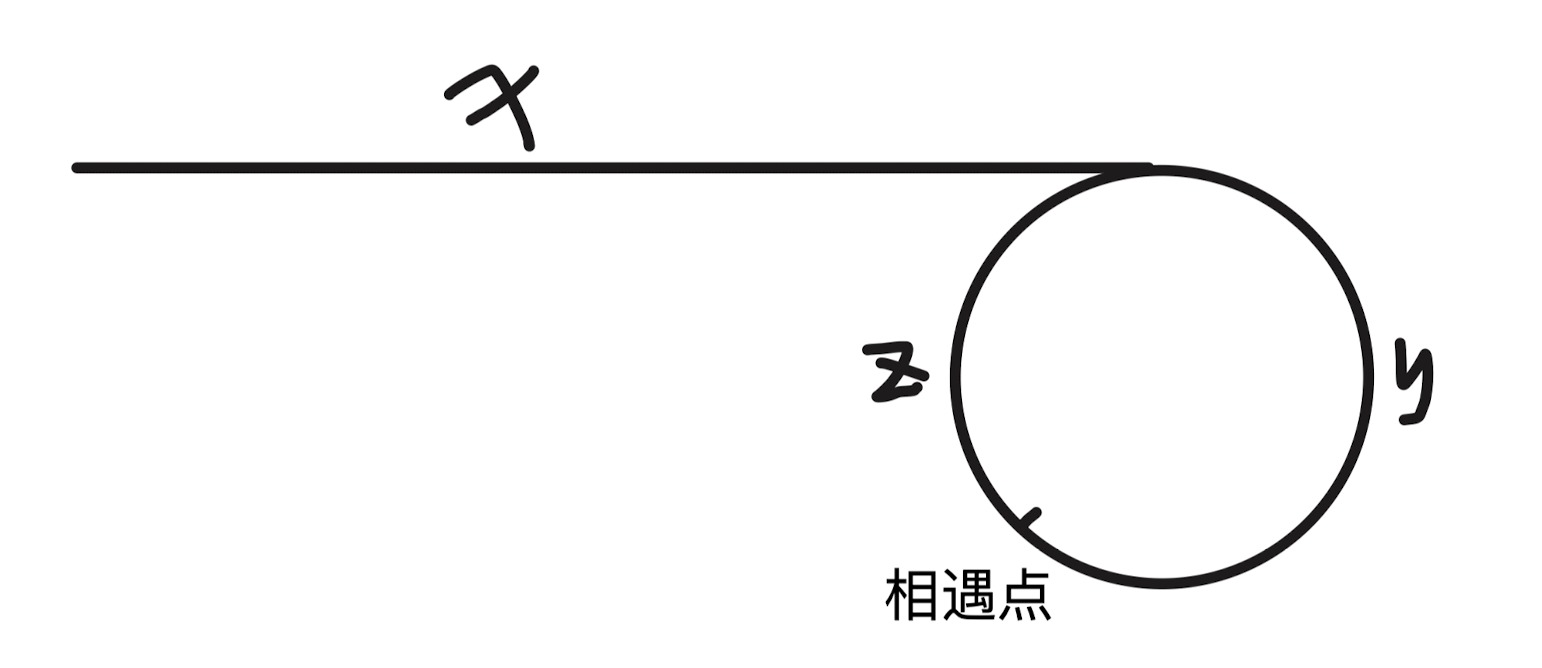
在这里插入图片描述

假设 n 为相遇前，快指针在环里转的圈数

相遇时走过的距离
对于慢指针：x + y
对于快指针：x + n * (y + z) + y

因为相遇时，循环次数是一样的，所以 x + y = [x + n * (y + z) + y] / 2
化简得 x = n * (y + z) - y
即 x = (n - 1) * (y + z) + z

所以当 index1 和 index2 同时从起点和相遇点出发，index2 在经过 n 圈后一定能和 index1 在入环点相遇

为什么慢指针在环里走不满一圈，就一定会被快指针追上？
假设极限情况，慢指针进入环时，快指针就在它前面一点点处。这种情况要追的距离最远。因为快指针的速度是慢指针的 2 倍，这样当慢指针要走完一圈时，快指针快走完两圈了，刚好比慢指针多一圈，也就是刚好能在入环点追上。此时慢指针还未走完一圈

双指针法代码：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;
        for (; fast != null && fast.next != null;) {
            slow = slow.next;
            fast = fast.next.next;

            // 存在环，则下面开始找入环处
            if (slow == fast) {
                ListNode index1 = head;
                ListNode index2 = slow;
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
             }
        }
        return null;
    }
}

也可以用哈希表法，巨简单，只是空间复杂度为 O(n)

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode pos = head;
        Set<ListNode> visited = new HashSet<ListNode>();
        while (pos != null) {
            if (visited.contains(pos)) {
                return pos;
            } else {
                visited.add(pos);
            }
            pos = pos.next;
        }
        return null;
    }
}