【三维点云的格式】1.2 PCA

初识

直观

PCA，pricipal components analysis，主成分分析

主成分(pricipal components)是一系列互相正交(orthogonality)的单位向量(unit vectors)，组成了正交基(orthonormal basis)。
PCA就是改变数据的正交基。

这些单位向量的方向通常是使得数据到该直线的的距离最小(minimize b)，或者数据到该原点的投影距离最大(maximize a)，即$minSS=a_1^2+a_2^2+...+a_n^2$。

确定好拟合直线，对该向量进行单位化，得到第一个主成分单位向量。然后根据该直线找到其正交的另一条直线，即可得到第二个主成分单位向量。

将这个正交基旋转合适的角度，重新画图，得到PCA后的数据。

专业术语 Terminology

• 数据在主成分
• $SS=Eigenvalue$
• $\sqrt{Eigenvalue}=Singular$
• unit vector = singular vector = eigenvector
• 单位向量的分量，如0.6、0.8，叫做 loading scores
• $\frac{SS}{(n-1)}=Variation，n为维数$
• 展示Variation的图，叫做 scree plot
• 
  
  扩展到三维数据，拟合得到红色的线，根据红色的线得到正交的蓝色、黑色，最终得到正交基。最终的结果是，两两相交得到一个正交基，在此基础上可以画图。

PCA的应用(Applications)

• Dimensionality reduction 降维
• Surface normal estimation 表面法向量估计
• Canonical orientation 规范方向
• Keypoint detection 关键点检测
• Feature description 特征描述

理解

Vector Dot Product 内积：

基变换：数据与基做内积运算，结果作为新的坐标分量。

Matrix-Vector Multiplication : Linear combination

$$\begin{array}{c}\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right)\left(\begin{array}{ccc}{x}_1& x_2& x_3\\ y_1& y_2& y_3\\ z_1& z_2& z_3\end{array}\right)=\left(\begin{array}{cc}{v}_{11}& v_{12}\\ v_{21}& v_{22}\end{array}\right)\end{array}$$
其中$a_{ij}$表示第$i$个主成分；$x_i{y}_i{z}_i$表示第$i$个原数据；$v_{ij}$表示第$j$个原数据投影到第$i$个主成分下的值
得到值的过程$v_{ij}=a_{i1}\ast x_j+a_{i2}\ast y_j+a_{i3}\ast z_j$是内积运算，即得到的值就是原始数据到主成分向量的投影

为什么选择距离最近<->投影距离最远
( the variance of the projected data points on that direction is maximal)

为了尽可能多的保存数据的原始信息，即使得数据变换后尽可能分散，如果数据过于集中，那么得到的数据单一而缺少意义

为社么后续主成分直接由垂直得到

在得到转变后的第一组和第二组数据之间，我们希望他们是线性不相关的(linearly uncorrelated)
如果二者有线性关系，数据过于相似，则是无效的
衡量两个数据之间的相关性是用的协方差，即为了使得协方差为0，尽可能保证原始数据的信息，减少信息丢失，主成分选择与前一个主成分正交的向量

公式

预备

covariance Cov 协方差：

Multivariate random variable 协方差矩阵：

Singular Value Decompositionm SVD 奇异值分解:

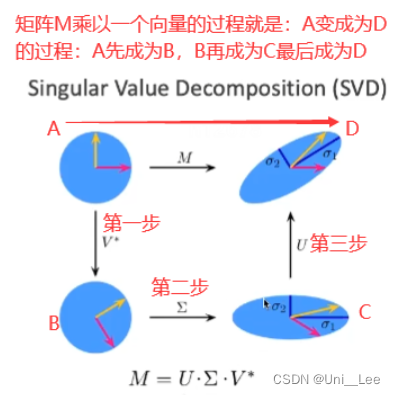
从SVD的角度去理解物理意义：比如说上图中的矩阵$M$，他可以被分解成$U\sum V^{\ast }$其中$U$和$V$都是一个正交矩阵(类似于旋转矩阵的东西)，$\sum$就是一个对角阵，他的对角线上储存了$M$的特征值，如果我把$M$乘以一个向量，第一步其实就是应用$V$在高维空间对这个向量做一个旋转，第一步这个圆被旋转了一下；第二步$\sum$就是对这个旋转后的向量在每一个维度上做一个缩放，所以这个圆就变成了一个椭圆；第三步：再应用$U$，也是高维空间上的旋转矩阵，所以我就把这个椭圆给旋转了一下。所以最后$M$乘以一个向量就是把这个圆变成了椭圆。

eigenvalue decomposition EVD 特征值分解:

$U$的每一列都是相互正交的特征向量，且是单位向量，满足$U^{T}U=I$ ，$\Lambda$对角线上的元素是从大到小排列的特征值，非对角线上的元素均为0。
旋转矩阵一定是对称的正交矩阵，单位正交矩阵，且行列式为1，即是旋转矩阵。

Rayleigh Quotients 瑞利熵：

所以瑞利熵说的就是我这个$A$最终能够拉长或者缩短我这个向量$x$多少倍，就是${\lambda }_{min}$和${\lambda }_{max}$是A的最小和最大特征值。
证明：

推导

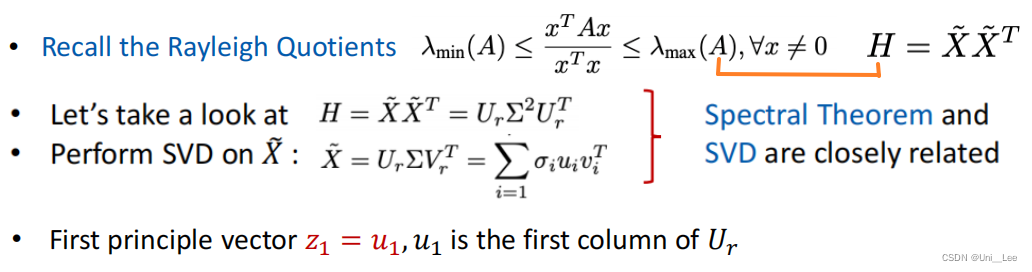
U是正交矩阵，所以u2正交与u1，即上述所说的确定好第一个主成分后，后面的主成分选择和他正交的

Kernel PCA

上述普通的PCA其实是一个线性的PCA，因为所谓的矩阵乘法也是一个线性操作而已，因为矩阵乘以向量其实是对矩阵列的线性组合。当遇到的数据不是线性时，可以选择先升到高维(high dimension)，再PCA。将原来二维空间的数据，升到三维空间，再做以划分。这个升维操作就叫做Kernel PCA。

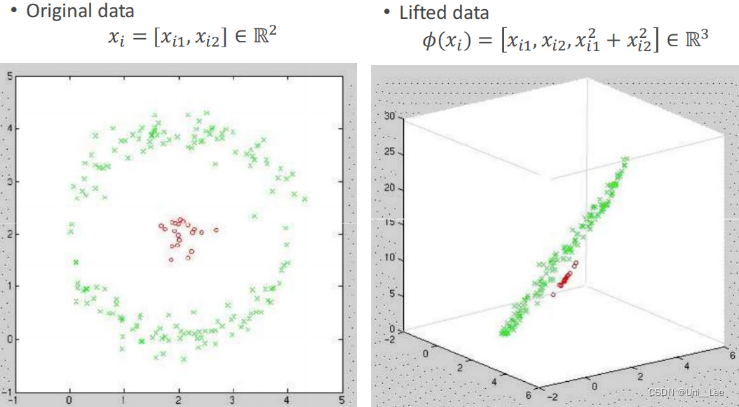
具体定义：

参考链接

1. StatQuest: Principal Component Analysis (PCA), Step-by-Step：https://www.youtube.com/watch?v=FgakZw6K1QQ
2. https://blog.youkuaiyun.com/m0_37957160/article/details/115350430
3. https://zhuanlan.zhihu.com/p/37609917
4. http://www.ams.org/publicoutreach/feature-column/fcarc-svd
5. https://blog.youkuaiyun.com/qq_40824311/article/details/102607966
6. https://zhuanlan.zhihu.com/p/59775730