【机器学习】之梯度下降算法（GradientDescent）

前言

关于梯度的前世今生问题我已经在这篇文章中探讨了 => 【机器学习】之梯度的探究
现在我们已经知道，一个函数在其梯度方向上变化率最大！

本篇是对黑猿大叔TensorFlow从0到1 - 6 - 解锁梯度下降算法的理解。

推导

因为函数C沿梯度方向变化率最高，我们不妨令

则此时ΔV的方向是梯度方向或者梯度反方向（为什么ΔV方向既可以是梯度方向也可以是梯度反方向呢）

我们的目标是：损失函数找到最小值！在函数C上从高往低走，自然有ΔC<0，故λ应取负值。
所以ΔV的方向与梯度方向相反！

回头再来看“最陡峭的一小步”的数学解释，那就是沿着梯度的反方向上走一小步。只要一小步一小步朝着正确的方向移动，迟早可以走到C(v1, v2, …, vn)的最小值处。“梯度下降”，名副其实。

令η = -λ，称η为学习率（learning rate）

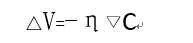
梯度下降的具体操作方法如下

随机选取自变量的初始位置v（以后会专门讨论初始化的技巧）；
v → v’ = v - η▽Cv（v移动到v’，▽Cv是v处的梯度，η保持不变）;
v’ → v’’ = v’ - η▽Cv’（v’移动到v’’，▽Cv’是v’处的梯度，η保持不变）;
…
v移动的次数，即训练的步数steps
v是各个自变量(v1, v2, …, vn)的向量表示，那具体到每个自变量该如何移动呢？以v1，v2为例：

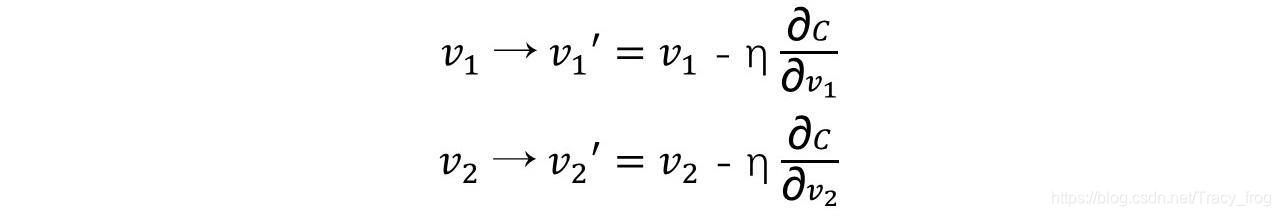
随机梯度下降算法

tensorflow实战训练

https://www.jianshu.com/p/042bb8d167d4

其他

• 为什么ΔV方向既可以是梯度方向也可以是梯度反方向呢？

梯度方向变化率最大可以理解，可是梯度反方向也是变化率最大吗？
此处不严谨地证一下，帮助理解。
前面我们已经推导出

梯度方向与向量l方向相同，则梯度反方向与向量l的方向也是相反的
cos[-gradf(x,y),e] = -1
则所求方向导数的值为梯度的模的相反数！
斜率的绝对值越大函数越陡峭 => 梯度方向和梯度反方向一样陡峭！

【参考资料】
TensorFlow从0到1 - 6 - 解锁梯度下降算法
tensorflow-梯度下降,有这一篇就足够了