Radar Installation

最新推荐文章于 2022-01-16 20:03:50 发布

原创最新推荐文章于 2022-01-16 20:03:50 发布 · 390 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种基于贪心算法的雷达覆盖优化方案，用于在海岛上安装最少数量的雷达装置，确保所有岛屿都能被有效覆盖。算法通过笛卡尔坐标系定位岛屿，考虑雷达覆盖距离，实现了最小化雷达数量的目标。

描述

假设滑行是无限直线。土地位于海岸线的一侧，另一侧是海洋。每个小岛都位于海边。并且位于滑行的任何雷达装置只能覆盖d距离，因此如果它们之间的距离最多为d，则可以通过半径装置覆盖海中的岛屿。

我们使用笛卡尔坐标系，定义滑行是x轴。海侧在x轴上方，陆侧在下方。考虑到每个岛屿在海中的位置，并考虑到雷达装置覆盖范围的距离，您的任务是编写一个程序，以找到覆盖所有岛屿的最小数量的雷达装置。注意，岛的位置由其xy坐标表示。

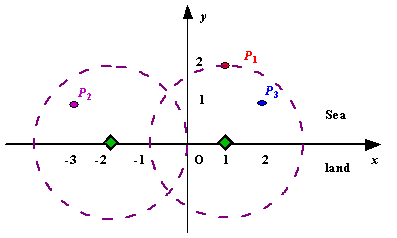
图A雷达装置的示例输入

输入

输入包含几个测试用例。每种情况的第一行包含两个整数n（1 <= n <= 1000）和d，其中n是海中岛屿的数量，d是雷达装置的覆盖距离。接下来是n行，每行包含两个整数，表示每个岛的位置坐标。然后是一个空白行来分隔案例。

输入由包含零对的行终止

产量

对于每个测试用例输出，一行包含测试用例编号，然后是所需的最少数量的雷达安装。“-1”安装意味着没有解决方案。

样本输入

<span style="color:#000000">3 2 
1 2 
-3 1 
2 1 

1 2 
0 2 

0 0
</span>

样本输出

Case 1: 2
Case 2: 1

想法：贪心题目，雷达在x轴上的话，把每个小岛的坐标按x从小到大的顺序排好，

遍历每个点的时候把点看做圆的左边界，得出雷达X的值，每次圈不住小岛的坐标的时候

更新X的值为那个点为左边界圆心的值。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1009;
int d,n;
struct point
{
    int x,y;
};
point p[N];

bool cmp( point a, point b){
    return a.x<b.x;
}

double getx(point a){
    return a.x+sqrt(1.0*d*d-1.0*a.y*a.y);
}
int main()
{
    int cas=0;
    while(~scanf("%d%d",&n,&d)&&(n+d)){  //输入n，d  ，0 0 的时候结束
        bool flag=0;
        for(int i=0;i<n;i++){
            scanf("%d%d",&p[i].x,&p[i].y);
            if(p[i].y>d)flag=1;     //直接淘汰：y>d的时候
        }
        if(flag){
            printf("Case %d: -1\n",++cas);
            continue;
        }
        sort(p,p+n,cmp);
        double x=getx(p[0]);   // x 是贪心出的雷达的坐标
        int ans=1;
        for(int i=1;i<n;i++){
            double tmp=getx(p[i]);
            if(p[i].x<x&&x>tmp){
                x=tmp;
                continue;
            }
            if(p[i].y*p[i].y+(p[i].x-x)*(p[i].x-x)<=d*d)
                continue;
            x = getx(p[i]);
            ans++;
        }
        printf("Case %d: %d\n",++cas,ans);
    }
    return 0;
}