本文介绍了二维图形变换，包括缩放、反射、切变、旋转及其矩阵表示。讲解了线性变换、齐次坐标的概念，并探讨了平移、仿射变换以及逆变换。还讨论了变换的组合、分解以及旋转矩阵的性质。
二维变换
缩放
在等比例缩放情况下
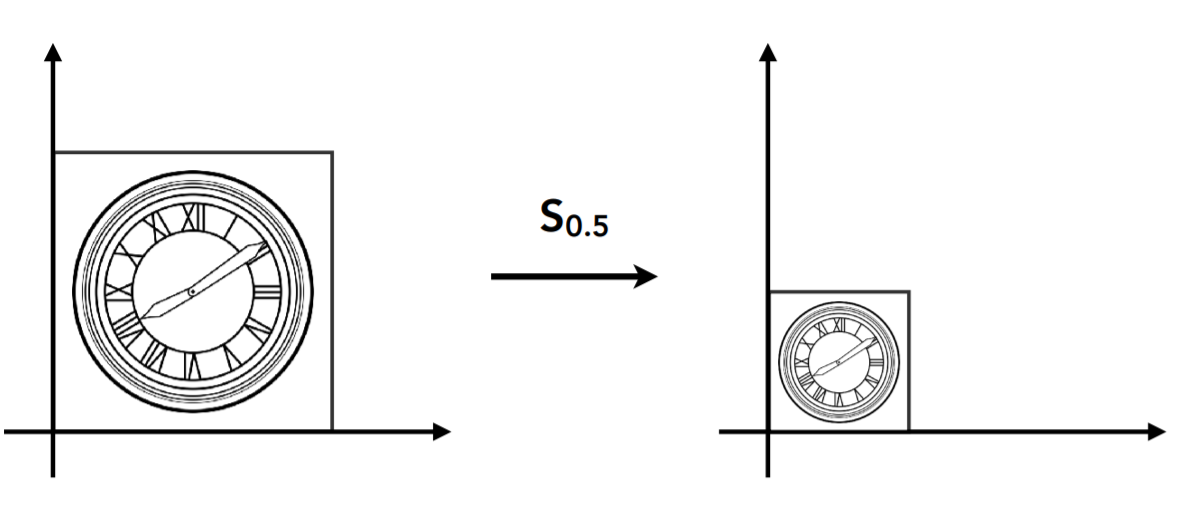
如上图所示，若将图片缩小两倍，则坐标 x , y x,y x,y的变换为
x ′ = s x y ′ = s y x'=sx \\ y'=sy x′=sxy′=sy
表示为矩阵形式
[ x ′ y ′ ] = [ s 0 0 s ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} s & 0 \\ 0 & s \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[s00s][xy]
非等比例缩放情况下
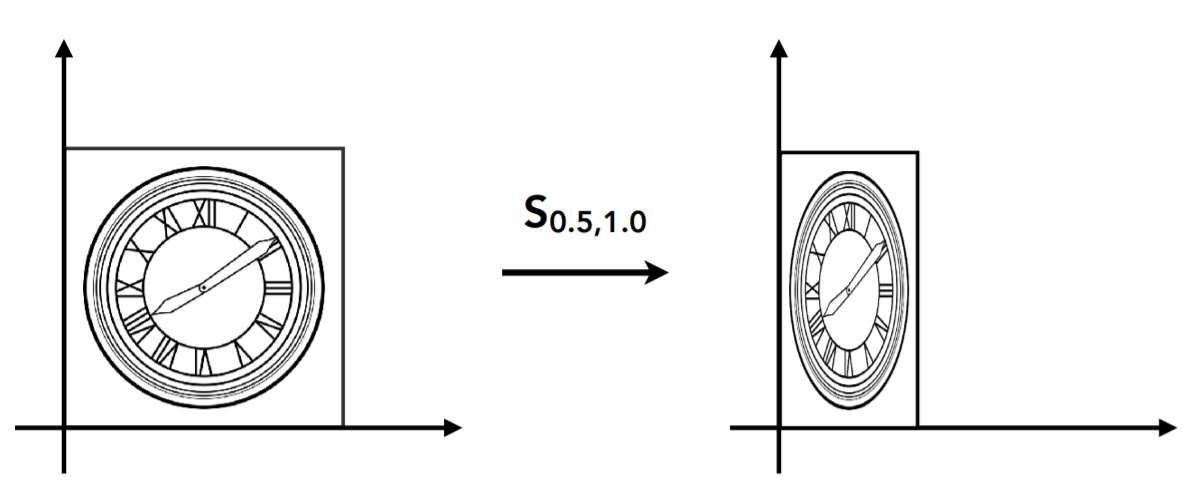
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} s_x & 0 \\ 0 & s_y \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[sx00sy][xy]
反射
水平翻转情况
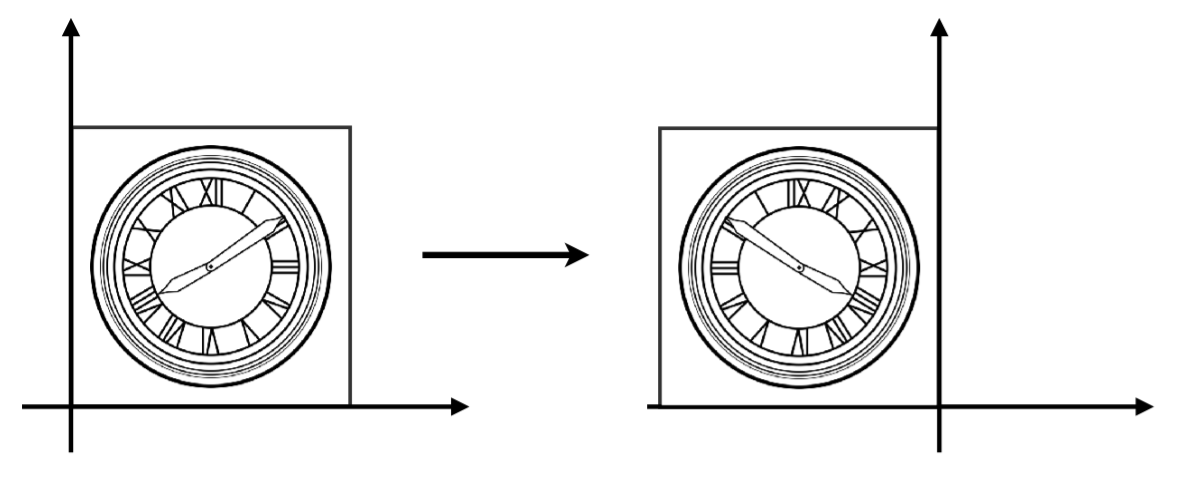
坐标关系
x ′ = − x y ′ = y x'=-x\\ y'=y x′=−xy′=y
写成矩阵形式
[ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} -1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[−1001][xy]
切变
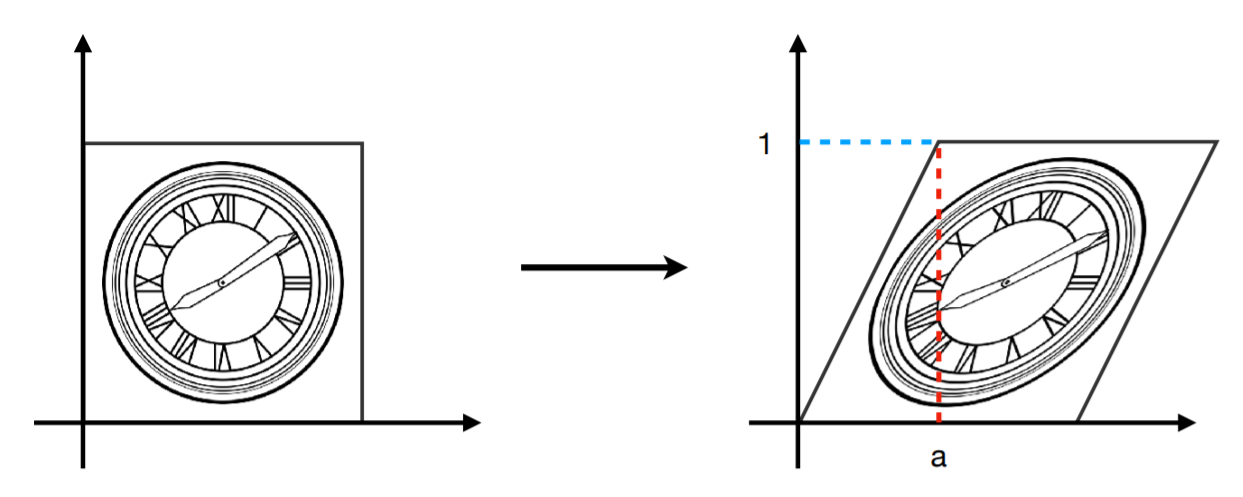
根据观察可发现坐标关系：
- 垂直方向上的坐标一直都没有发生变化
- 当 y = 0 y=0 y=0时， x , y x,y x,y坐标都无变化
- 当 y = 1 y=1 y=1时， x x x坐标都平移了 a a a
写成矩阵形式
[ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[10a1][xy]
旋转
默认情况下，旋转都是绕着圆点旋转，旋转方向为逆时针。
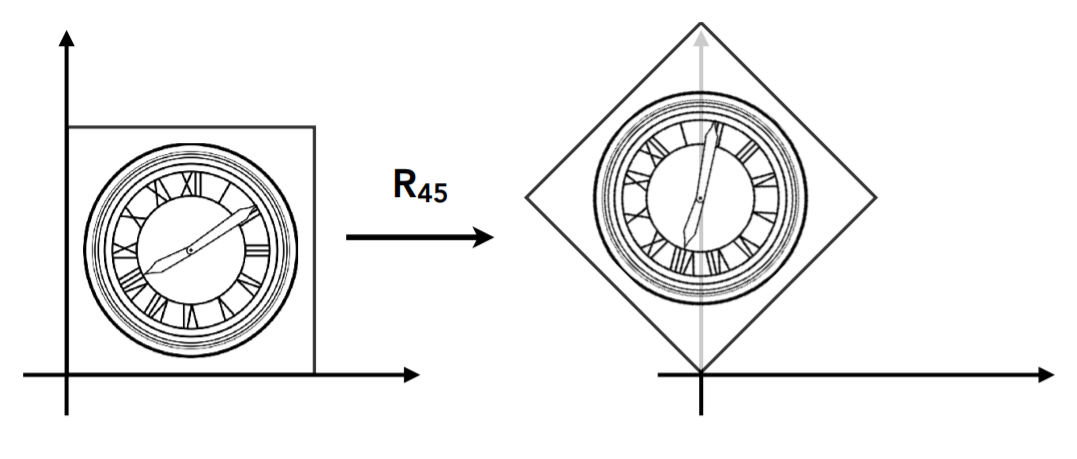
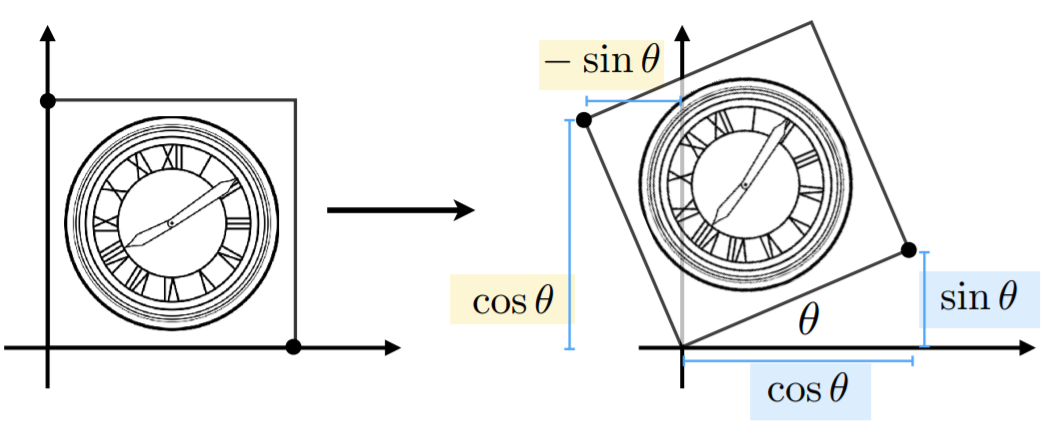
旋转矩阵
R θ = [ cos θ − sin θ sin θ cos θ ] R_{\theta}=\left[\begin{array}{ll} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right] Rθ=
最低0.47元/天 解锁文章
扫一扫
703
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
