一:运动学建模
根据四足机器人的机械模型,测量出机械腿的关节间距,根据关节间距建立D-H模刑。
D-H模型主要应用于机器人运动学,在每个连杆上建立一个坐标系,通过齐次坐标变换,便可建立首末坐标系的关系。
记舵机1到舵机2的轴间距为L1,舵机2到舵机 3的轴间距为L2,舵机3到腿末端的轴间距为L3,关节夹角1为01,关节夹角2为02,关节夹角3为03,建立D-H参数表。

二:正运动学解算
建立D-H表后,进行正运动学解算,建立关节夹角与足端坐标的方程。首先根据D-H表得出齐次变换矩阵。随后将矩阵相乘,取矩阵的第四列,完成正运动解算计算结果如下所示。
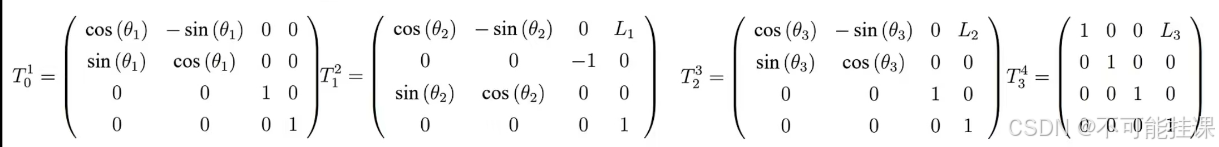
![]()
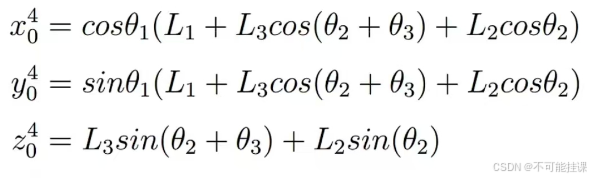
三:逆运动学解算

四:机身姿态解算
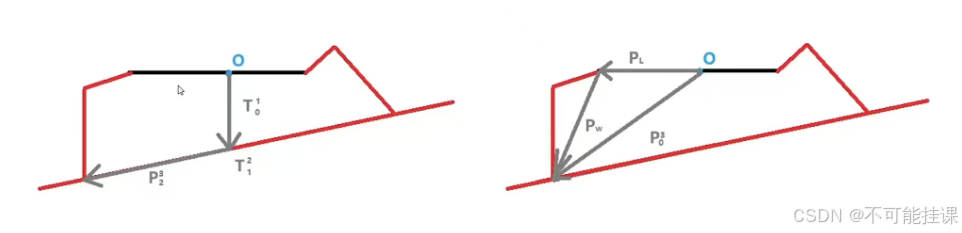
记PL为机身中心到腿起始端的向量,Pw是腿起始端到足端的向量,P是机身中心O到足端的向量Ps为站立状态下的腿起始端到足端的向量.
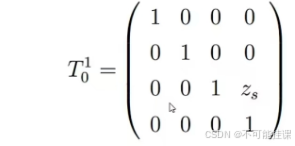
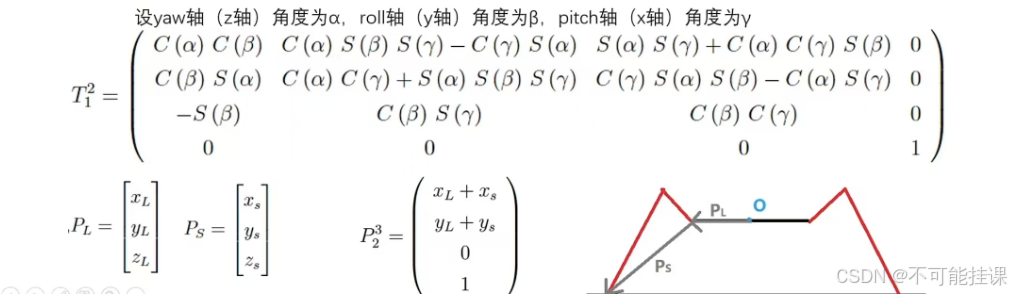
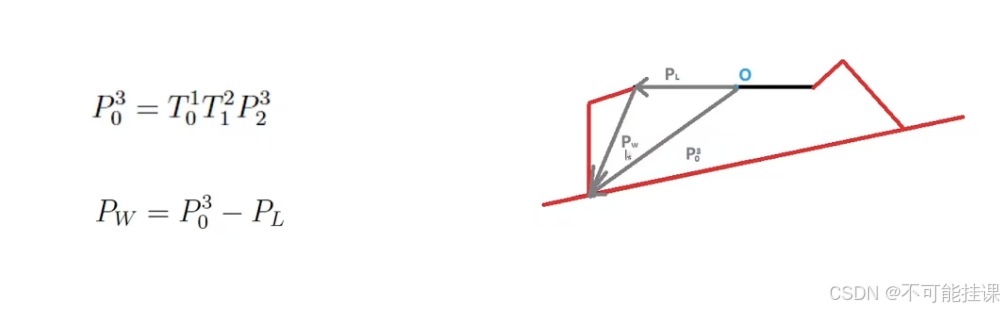
五:机身位置控制
记机身位置为PB,Pw是腿起始端到足端的向量,Ps为站立状态下的腿起始端到足端的向量
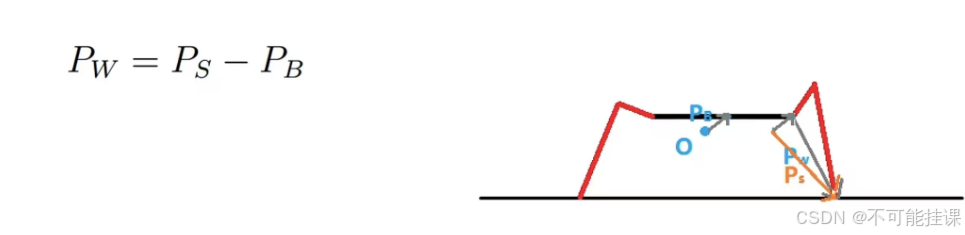
六:步态
四足机器人在四脚着地时是消极稳定的状态,走路时则不一定。如果每次只动一只脚,让其他三只脚仍稳稳地踩在地上,即是消极稳定状态,然而四足机器人也可以放弃此状态,进入积极稳定状态,这样可以动得比较快。这两种步态分别被称作爬行与快步。
这里我们使用爬行作为四足机器人运动的步态,运动过程中必须保证每次移动的时候都有三只脚踩在地面上,且重心放在这三只脚形成的三角形内,如果重心离开这个三角形太久,机器人就会跌倒。如下图所示:
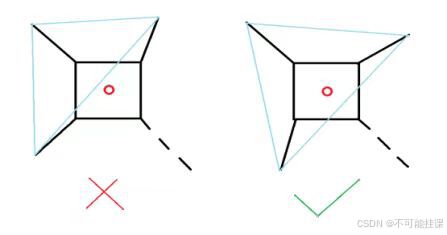
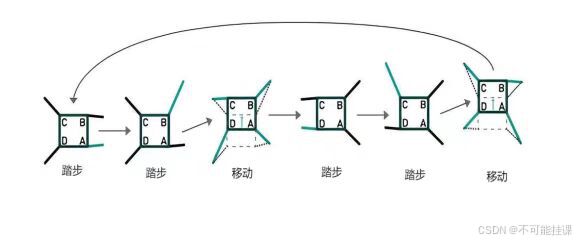
七:全向行走+转弯的数学原理
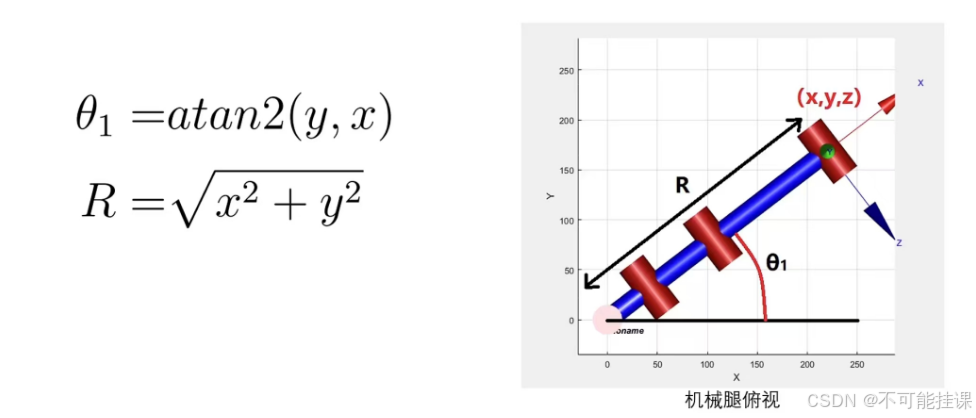
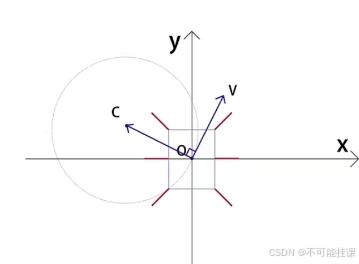
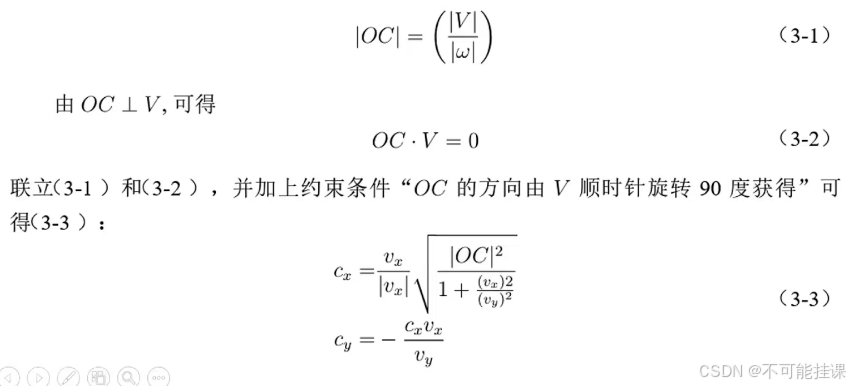
记机器人移动时线速度为 V,角速度为w,VX,VY分别是机器人x轴和y轴方向的速度,w是机器人的角速度。向量OC垂直于向量,且规定 OC的方向由V顺时针旋转90度获得。
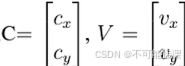




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








