2020张宇1000题【好题收集】【第八章：常微分方程】

基本知识

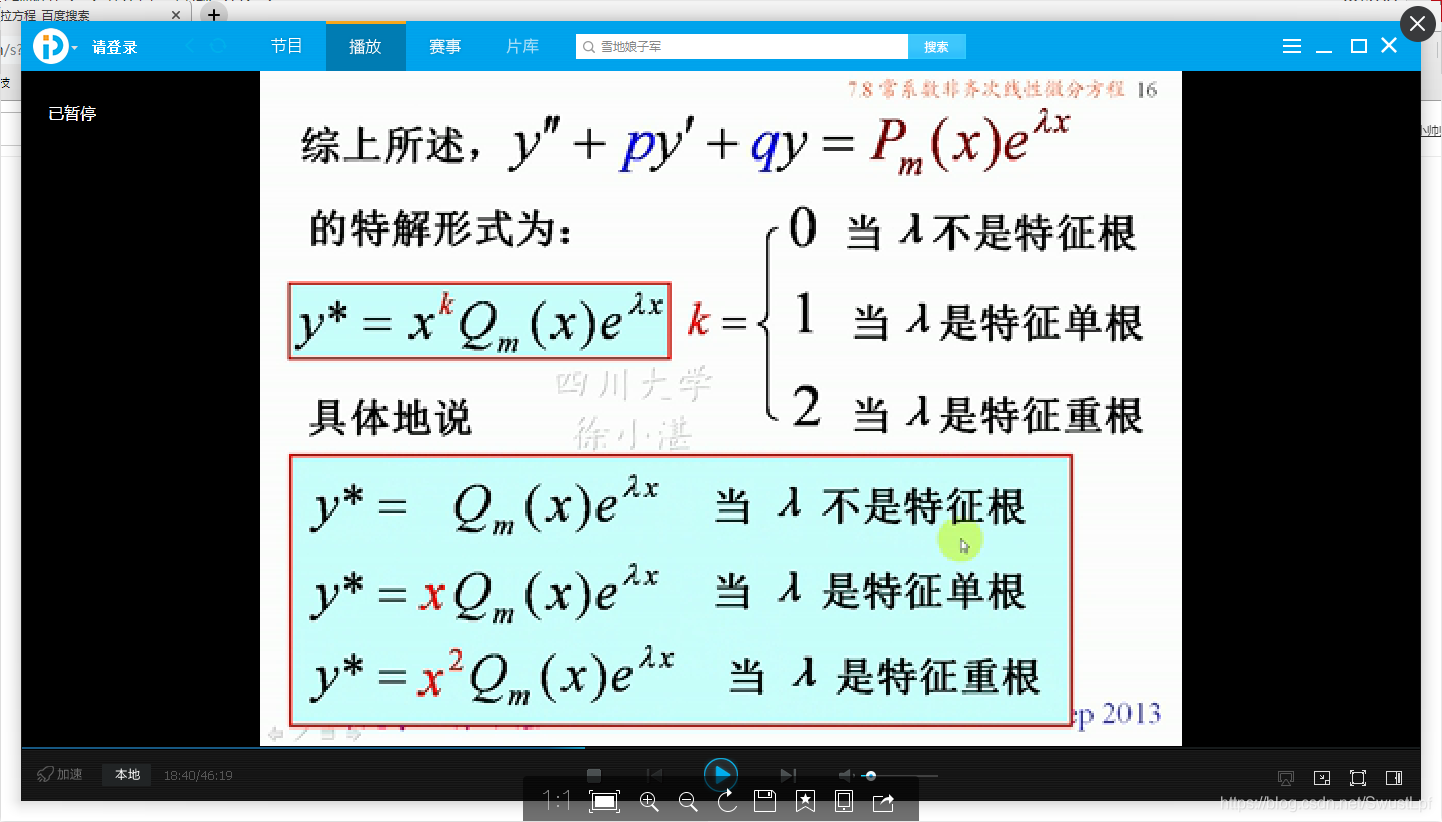
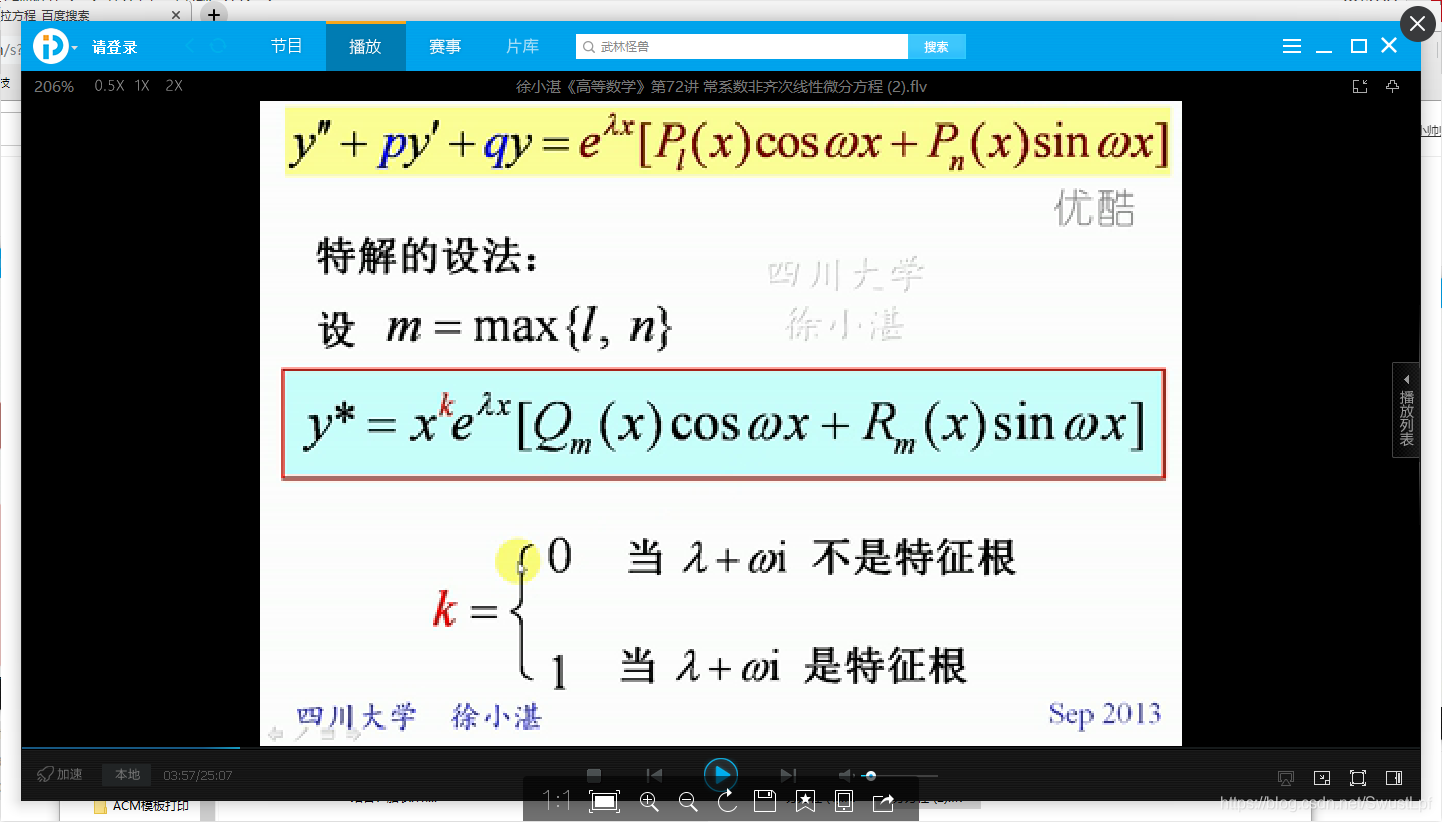
一阶常微分方程通解

$$y^{\prime }+p(x)y=q(x)$$
令$A(x)=e^{\int p(x)dx}$
$$y=\frac{1}{A(x)}(\int A(x)q(x)dx+C)$$

伯努利方程

$$y^{\prime }+py=q{y}^n$$
解法：
同时除以$y^n,然后把y^{-n}拿到微分里面去变成\frac{d(y^{(1-n)})}{dx}+p{y}^{(1-n)}=q$

欧拉方程

$$x^n{y}^{(n)}+p_1{x}^{n-1}{y}^{(n-1)}+...+p_{n}y=q$$
解法：
令$x=e^t$
然后令$D^n=\frac{d^{n}y}{d{x}^n}$
$$x^n{y}^{(n)}=D(D-1)(D-2)...1\cdot y$$

8.4【处理绝对值】

$$求\frac{dy}{dx}=(1-y^2)tanx的通解及特解,y(0)=2$$
很明显这个是可分离变量的，把$(1-y^2)$除过去

但是坑的地方是：要考虑$1-y^2=0$的时候
所以$y=1和y=-1$也是方程的解

因为会出现对数，所以要加绝对值，然后就是处理绝对值的问题了
$$\left|\begin{array}{c}\frac{1+y}{1-y}\end{array}\right|=\frac{e^{2C_1}}{co{s}^{2}x}把正负号拿到上面常数上\Rightarrow \frac{1+y}{1-y}=\frac{\pm e^{2C_1}}{co{s}^{2}x},然后再把\pm e^{2C_1}当作新的常数C\Rightarrow \frac{1+y}{1-y}=\frac{C}{co{s}^{2}x}$$
如果在代绝对值的时候就来确定常数的话，就有阔能出现双值$y$，这样就错了

8.5

$$xdy=(y-\sqrt{x^2+y^2})dx且y(1)=0,(x>0)$$
我一看，哎呀，形式好复杂啊，怎么搞？
观察一哈，虽然有平方，但是有根号呀，所以他们的次数都是1次的

变个形：
$\frac{dy}{dx}=\frac{y}{x}-\sqrt{1+(\frac{y}{x}{)}^2}$

$令u=\frac{y}{x},y=ux$

$\therefore dy=xdu+udx\Rightarrow \frac{dy}{dx}=x\frac{du}{dx}+u$

$\frac{1}{\sqrt{1+u^2}}du=-\frac{1}{x}dx$

左边是要记到的常用积分
$ln|u+\sqrt{1+u^2}|=-ln|x|+C$

8.8

$$(4-x+y)dx-(2-x-y)dy=0$$
这个是以前学的时候没怎么遇到的套路
$\frac{dy}{dx}=\frac{x-y-4}{x+y-2}$
$令\{\begin{array}{c}x=X+k\\ \\ y=Y+h\end{array}$

带入方程变成：
$$\frac{dy}{dx}=\frac{X-Y+k-h-4}{X+Y+k+h-2}$$
如果方程能变成$\frac{dy}{dx}=\frac{X-Y}{X+Y}$这样是不是就好解多了喃
其实就是当$\{\begin{array}{c}k-h-4=0\\ \\ k+h-2=0\end{array}$的时候，方程就变成上面那样了
上面那个就变成$$\frac{dY}{dX}=\frac{1-}{1+\frac{Y}{X}}$$