kkksc03考前临时抱佛脚

最新推荐文章于 2025-10-21 19:00:00 发布

原创最新推荐文章于 2025-10-21 19:00:00 发布 · 717 阅读

2 ·

CC 4.0 BY-SA版权

刷题专栏收录该内容

39 篇文章

订阅专栏

博客讨论了一个关于如何以最短时间完成多科作业的问题。初始尝试使用贪心算法解决，但发现并不适用，因为局部最优解不保证全局最优。于是转向动态规划的01背包问题来寻找解决方案，通过将每道题视为价值和重量相等的物品，求解最接近每科作业总时间一半的解，最后得到每科的最小完成时间并累加，得出整体的最短时间。

题目背景

题目描述

输入格式

输出格式

输出一行,为复习完毕最短时间。

输入输出样例

输入 #1

输出 #1

说明/提示

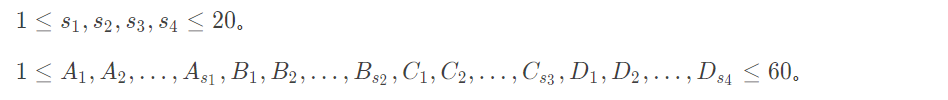
题目链接：https://www.luogu.com.cn/problem/P2392

题意：kkksc可以同时做两道题，两道题必须是同一科的。现在有4科作业，每科作业分别有s1,s2,s3,s4道题。求kkksc完成所有作业所需的最少时间。

注意：kkksc可以同时做两道题，但对于完成一道题，kkksc花费的时间并不会减半。

思路分析：看到这道题第一反应是贪心，对于同一科作业只需要把完成所有题花费的时间分成两份t1,t2，使这|t1-t2|最小，然后该科花费的最少时间就是max{t1,t2}。

贪心代码：

#include<bits/stdc++.h>
using namespace std;
int a[5],i,j,sum1,sum2,t,homework;
int main(){
    for(i=1;i<=4;i++)
        cin>>a[i];//输入
    for(i=1;i<=4;i++){
    sum1=sum2=0;//两边脑子时间清零
    for(j=1;j<=a[i];j++)
        {cin>>homework;
        if(sum1<=sum2) sum1+=homework;
        else sum2+=homework;}//哪边时间短就加在哪边
        t+=max(sum1,sum2);//取较长时间累加
    }cout<<t;//输出
    return 0;
}

提交后就WA了，显然对于本题，贪心不是最优解。在求解的过程中保持t1和t2近似相等，最终求解出的结果是不是最优的，因为本题局部最优不能推出全局最优，最终最优的结果是与选取的所有题有关的，而求解的过程中实现的最优解只是与当前状态所选取的所有题有关的。

要使用动态规划求解（01背包），设DP[]为数组，将背包的大小设置为单科所有题的时间总花费T的一半T/2，然后把题看作重量为t，价值为t的物品（t为该题花费的时间），这样就可以求出最接近T/2的数。最后求出的DP[T/2]就是最接近T/2的时间花费。最终结果是取最接近T/2中较大的那个，所以结果是 max{DP[T/2],T-DP[T/2]}

#include<bits/stdc++.h>
using namespace std;
int a[100];
int dp[1300];
int check(int sum,int n)
{
    if(n==1)
        return sum;
    memset(dp,0,sizeof(dp));
    for(int i = 0;i<n;i++)
    {
        for(int j = sum/2;j>=a[i];j--)
        {
            dp[j]=max(dp[j],dp[j-a[i]]+a[i]);
        }
    }
    return dp[sum/2]>sum-dp[sum/2]?dp[sum/2]:sum-dp[sum/2];
}
int main()
{
    int s1,s2,s3,s4,x;
    cin>>s1>>s2>>s3>>s4;
    int ans = 0;
    int sum = 0;
    for(int i = 0; i<s1; i++)
    {
        cin>>a[i];
        sum+=a[i];
    }
    ans+=check(sum,s1);
    sum = 0;
    for(int i = 0; i<s2; i++)
    {
        cin>>a[i];
        sum+=a[i];
    }
    ans+=check(sum,s2);
    sum = 0;
    for(int i = 0; i<s3; i++)
    {
        cin>>a[i];
        sum+=a[i];
    }
    ans+=check(sum,s3);
    sum = 0;
    for(int i = 0; i<s4; i++)
    {
       cin>>a[i];
        sum+=a[i];
    }
    ans+=check(sum,s4);
    cout<<ans<<endl;
    return 0;
}