系列文章目录
【1】开闭环系统及系统稳定性分析
【2】系统分析实例—Simulink建模仿真
【3】终值定理和稳态误差
【4】根轨迹快速全面掌握
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
提示:这里可以添加本文要记录的大概内容:
✅ 什么是根轨迹?(通俗解释)
根轨迹就是用来画出:
“当你调节系统增益时,系统的极点(本质上决定系统稳定性和响应速度的关键参数)会如何移动”。
换句话说:
它像是一幅地图,告诉你控制器参数一变,系统行为怎么变。
✅ 为什么我们关心“根轨迹”?
在自动控制里,我们最关注两个问题:
- 系统稳不稳定?
- 系统快不快、稳不稳、抖不抖?
而这些问题的答案,藏在系统的极点里!极点的位置不同,系统表现就完全不同:
| 极点位置 | 控制系统表现 |
|---|---|
| 实轴左边 | 稳定 |
| 越靠近虚轴 | 响应越慢 |
| 有虚部(成对共轭) | 有振荡 |
| 实轴右边 | 不稳定(爆炸) |
✅ 根轨迹的直白例子
🎯 例子:你设计一个电动机速度控制系统
你现在要让一个电动机在1秒内达到指定转速,而且不能“冲太猛”或者“抖得厉害”。
你用一个比例控制器(P控制),控制器的“增益K”你可以调。
你希望通过调整K让系统变得快又稳。
这时就需要用根轨迹图来判断:
- 如果K太小 → 电机响应慢
- 如果K适中 → 电机快速、平稳到达目标值 ✅
- 如果K太大 → 电机响应太快导致震荡、过冲甚至不稳定 ❌
你可以画出系统的根轨迹图,观察在不同的K值下,极点怎么走。然后选一个合适的K值,把极点安排到一个“你想要的性能区”里。
🧠 可以理解为:
调K就像调电机的“性格”:
K小 = 温吞;K适中 = 理智果断;K太大 = 脾气暴躁爱冲动 🤯
✅ 根轨迹在专业中的具体应用场景
-
伺服电机位置控制:
- 在光学平台或精密仪表中,伺服系统必须精准定位。根轨迹能帮助你选择合适的控制器参数,使系统快速响应又不抖动。
-
智能温控系统:
- 在恒温箱或热处理系统中,温度变化不能太慢(等不起),也不能太快(容易超温)。根轨迹图可以告诉你怎么调控制器,才能又快又稳达到目标温度。
-
电压/电流控制(比如变频器):
- 你设计电源模块时,希望输出电压能迅速稳定地达到设定值,不要来回震荡。这种动态性能调节就得靠根轨迹判断增益调到多少合适。
-
系统设计前的可视化分析:
- 根轨迹图像化强,它可以直观看出系统是否可能变成不稳定,是你调系统时的好帮手,特别适合仪器仪表控制精度要求高的场景。
✅ 总结一句话版(面试/答题可用):
根轨迹是分析和设计控制系统性能的重要工具,通过观察系统极点随增益变化的轨迹,帮助我们选择合适的控制器参数,使系统既稳定又响应良好。
如何绘制根轨迹图
-
确定系统的传递函数:
假设我们有一个简单的控制系统,其传递函数为:
G(s)=K/s(s+2) 这里,K 是增益。 -
找出系统的极点和零点:
- 极点:s=0 和 s=−2
- 零点:没有零点(因为分子没有s项)
-
绘制极点和零点:
在复平面上标出极点和零点:- 极点在 s=0 和 s=−2 处。
- 没有零点,所以不需要标出。
-
确定根轨迹的起始和结束点:
- 根轨迹从极点开始,向零点或无穷远延伸。在这个例子中,由于没有零点,根轨迹将从极点出发,向无穷远延伸。
-
使用根轨迹规则:
- 根轨迹在实轴上存在的区域由极点和零点之间的奇偶性决定。这里,实轴上从 s=0 到 s=−2 的部分是根轨迹的有效区域。
-
绘制根轨迹:
- 从 s=0 开始,根轨迹向左移动,经过 s=−2,然后继续向左延伸到无穷远。
示例图的描述
- 横轴:表示实部(Re)
- 纵轴:表示虚部(Im)
- 极点:在 s=0 和 s=−2 处用“×”标记
- 根轨迹:从 s=0 开始,沿着实轴向左延伸,经过 s=−2,然后继续向左延伸到无穷远。
如果你有绘图软件(如 MATLAB、Python 等),可以使用这些工具来生成根轨迹图。以下是一个简单的 MATLAB 代码示例,可以帮助你绘制根轨迹:
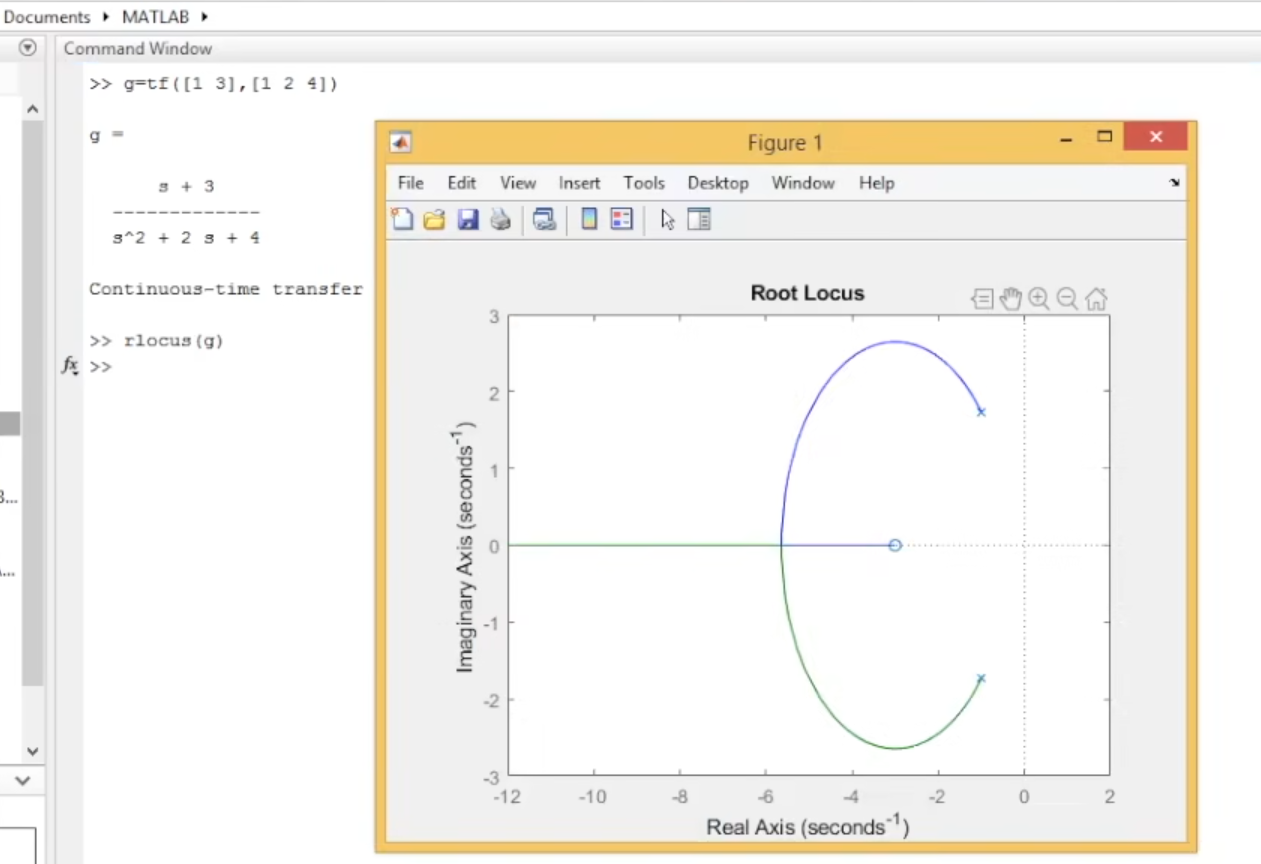
提示:以下是本篇文章正文内容,下面案例可供参考
一、根轨迹——“根”的作用
大清朝已经亡了,现在几行代码就可以搞定,掌握根轨迹手绘意义不大(但不代表完全不用学),所以重点应该放在掌握根的变化规律,从而可以设计控制器或者补偿器
根轨迹中“根”和极点是一样的概念
1.1 一阶系统
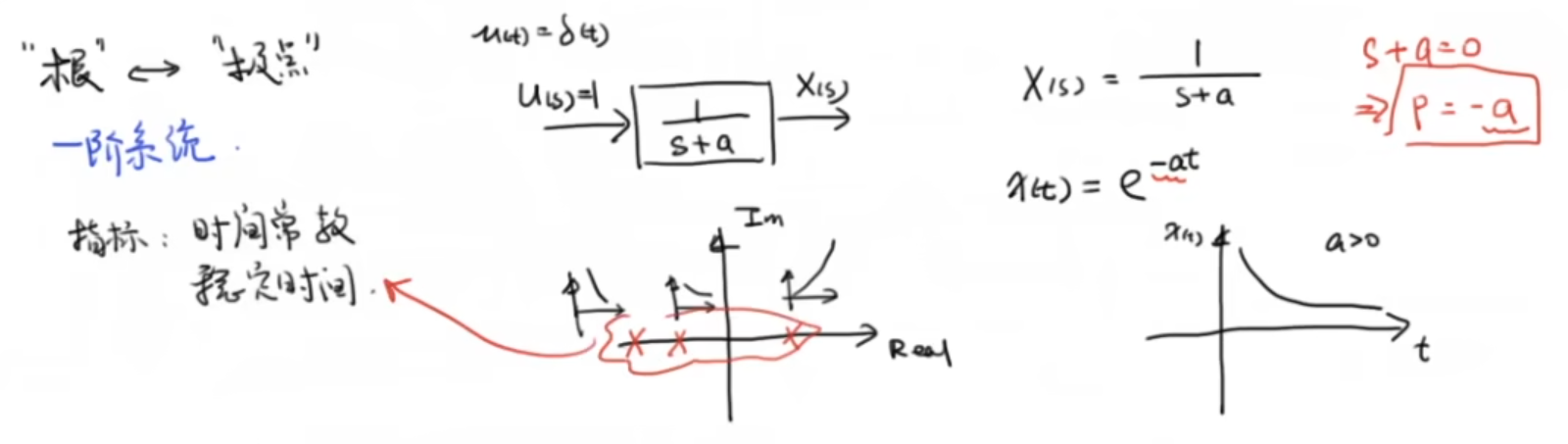
1.2 二阶系统
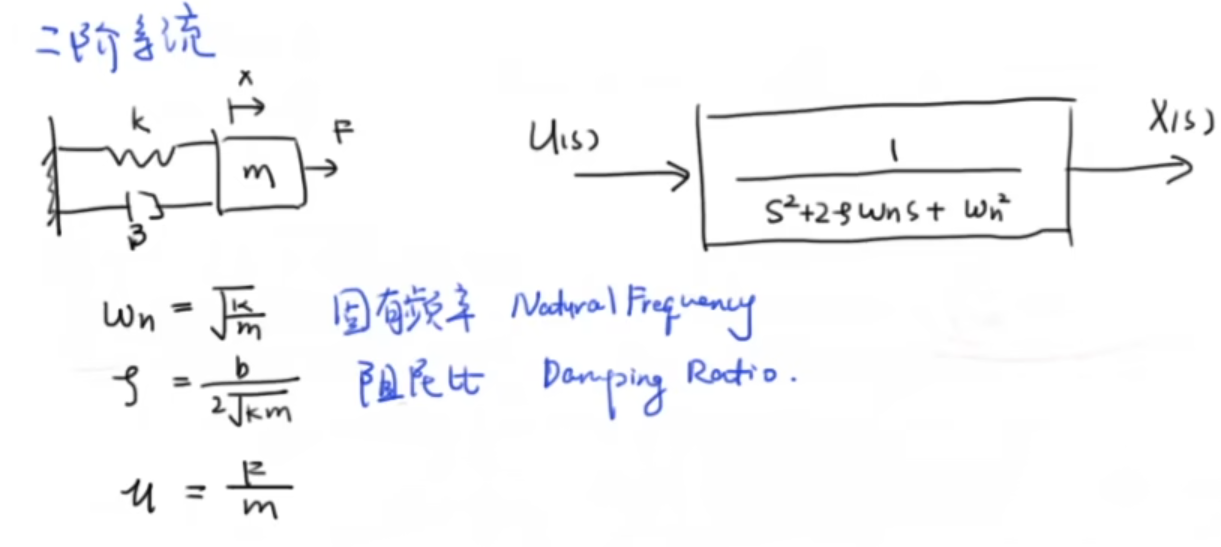
写出系统传递函数,求极点P1 P2,分情况讨论极点位置
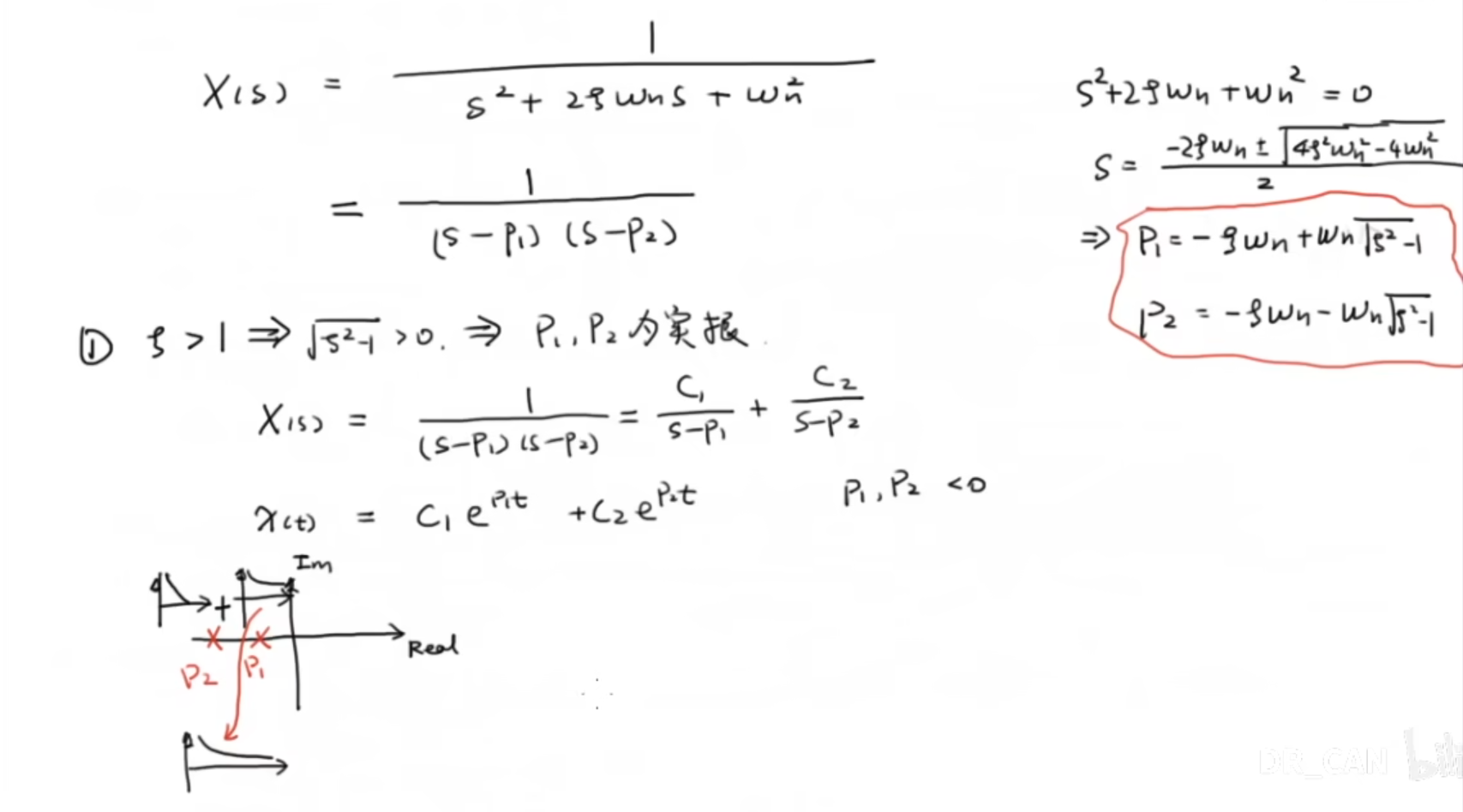
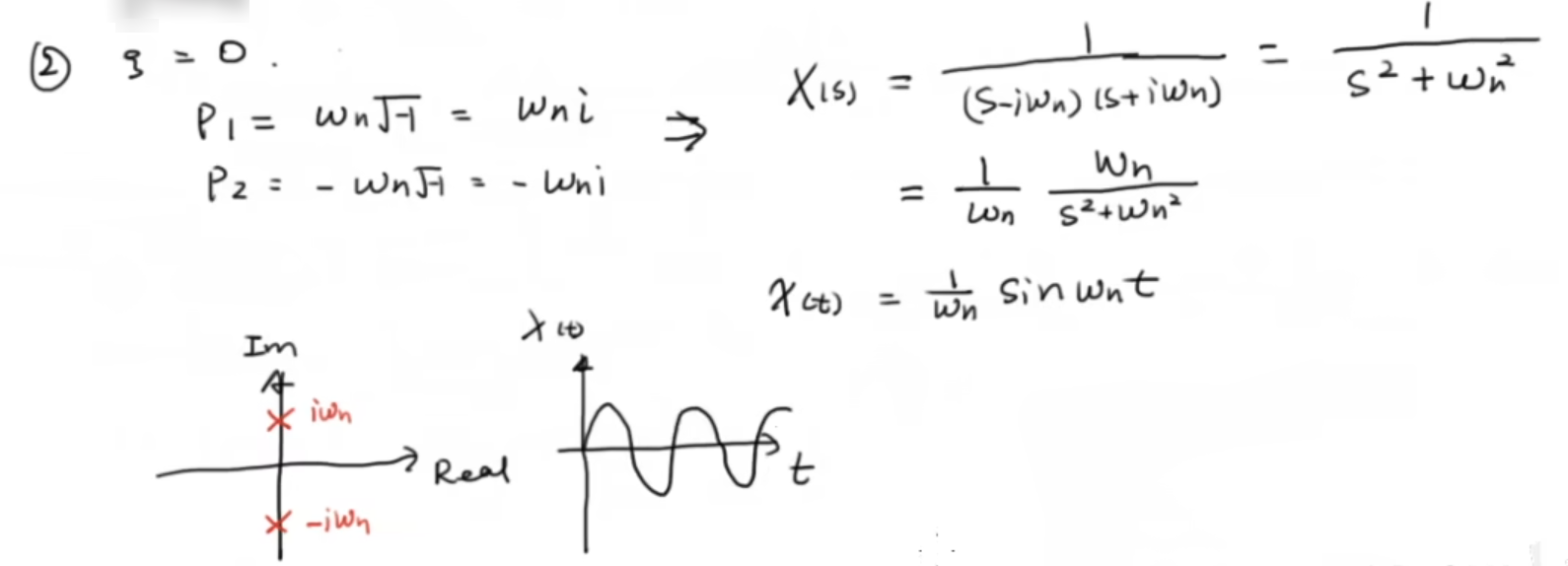

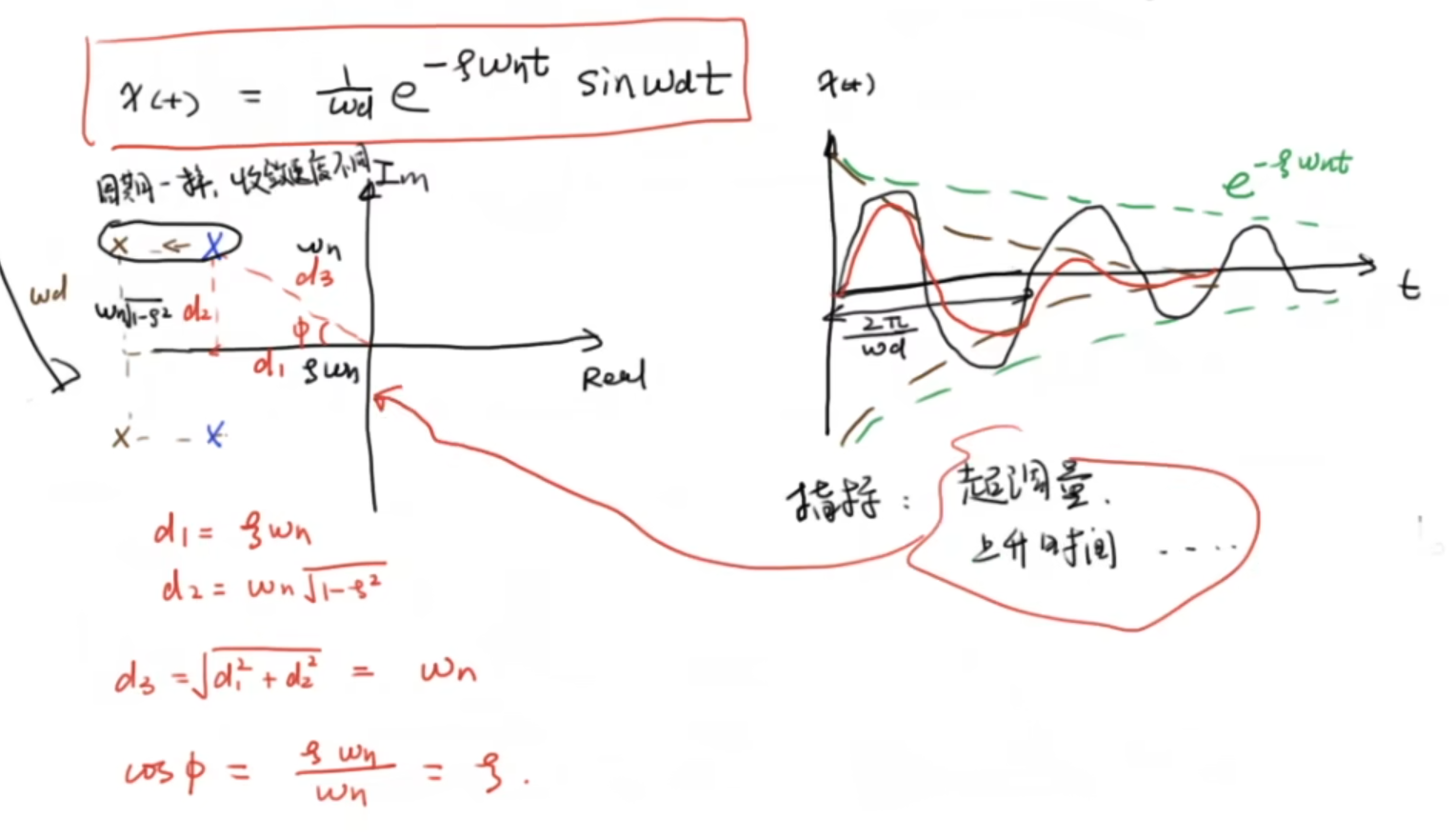
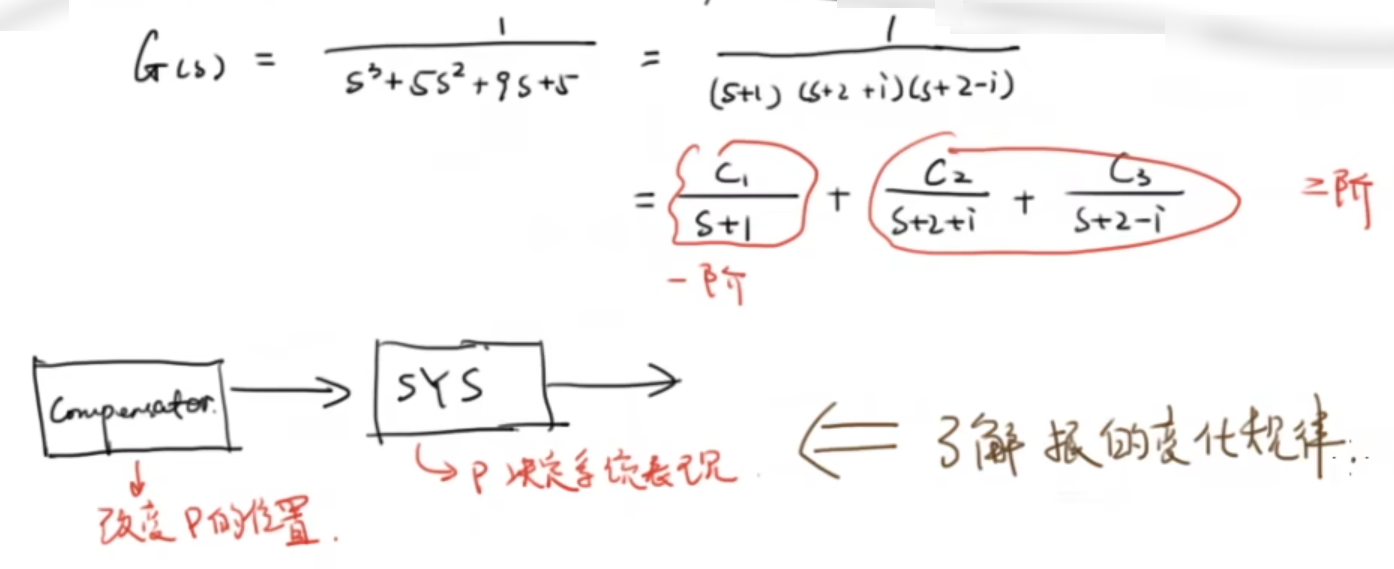
1.3 更高阶系统
更高阶系统不过就是一阶、二阶系统的叠加。
二、根轨迹——手绘技巧
2.1 根轨迹的基本形式
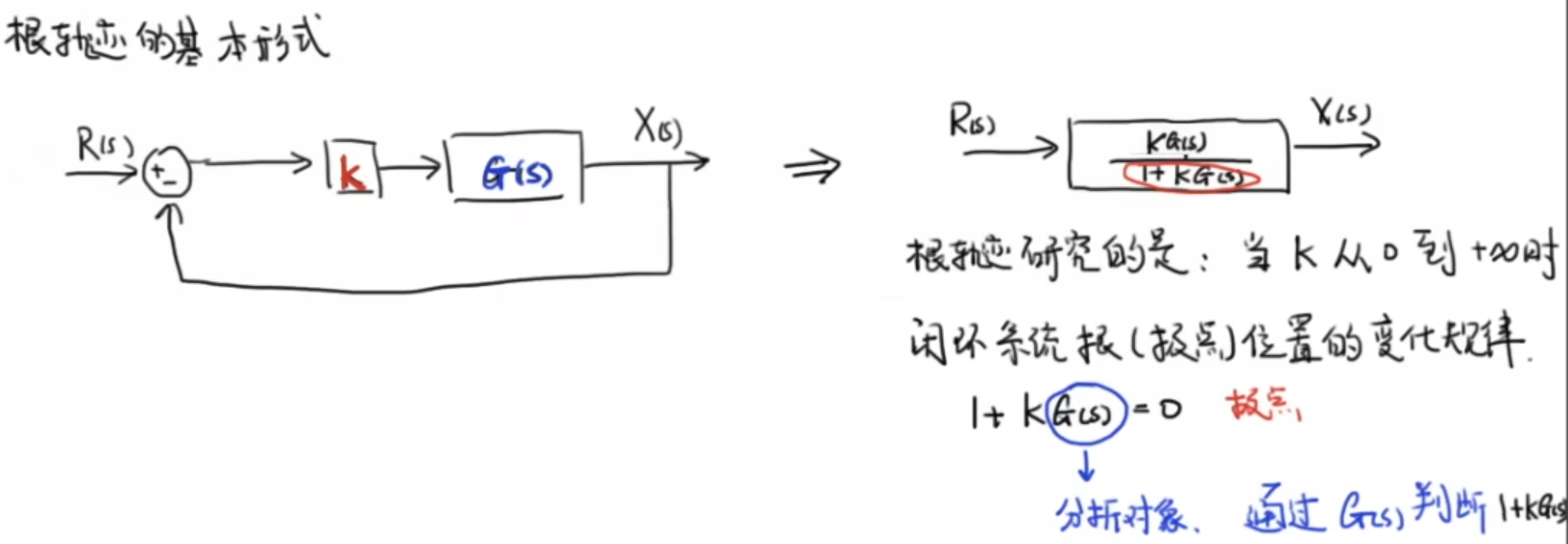
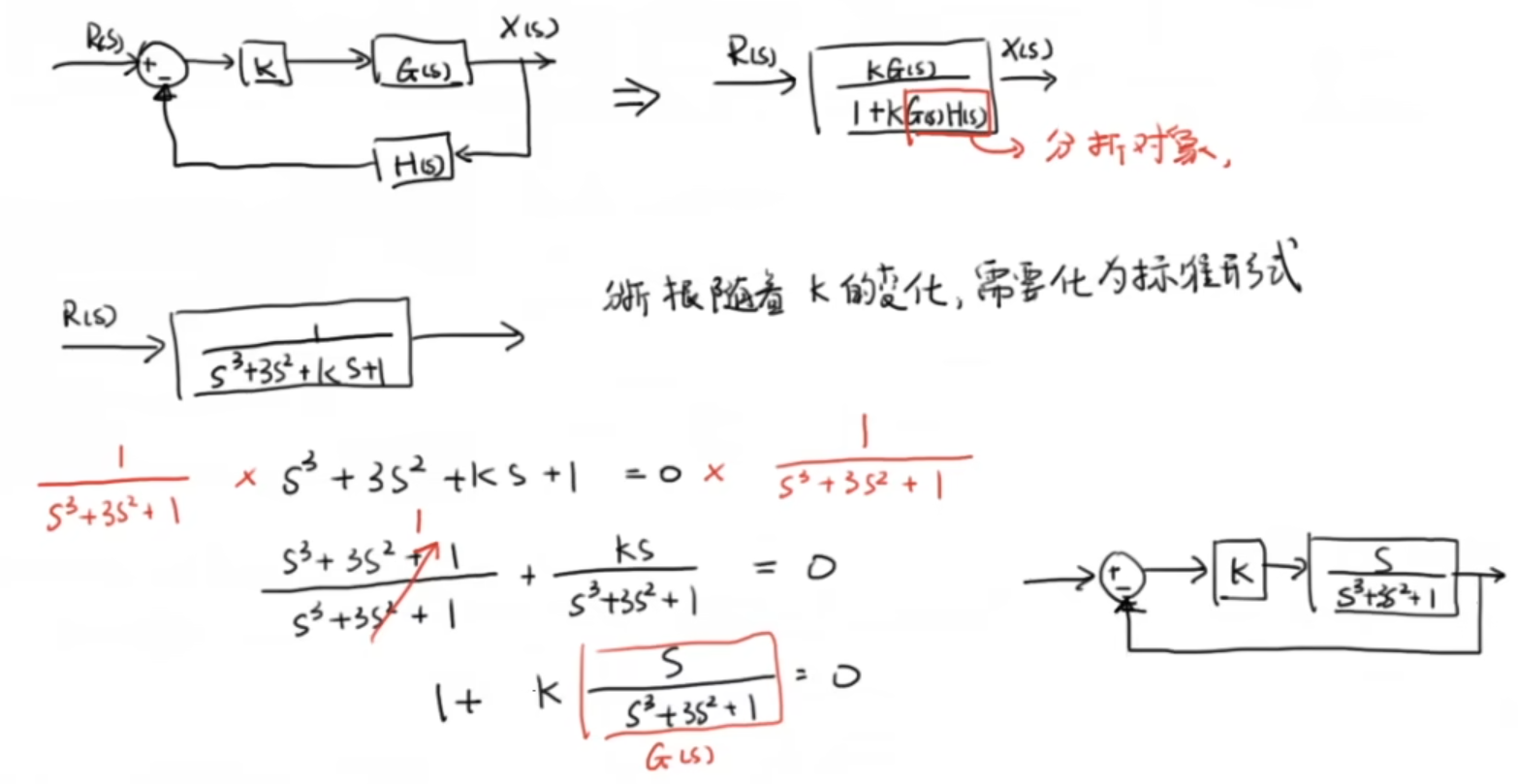
2.2 根轨迹规则



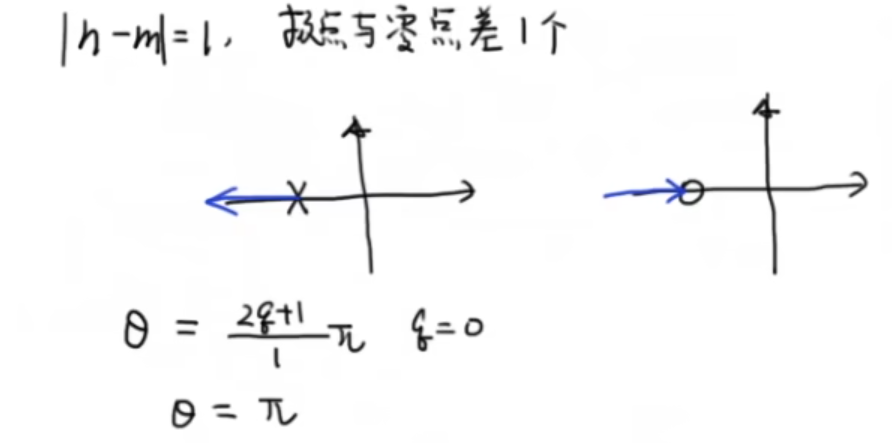
下面看一个综合的例子:

在matlab中验证:

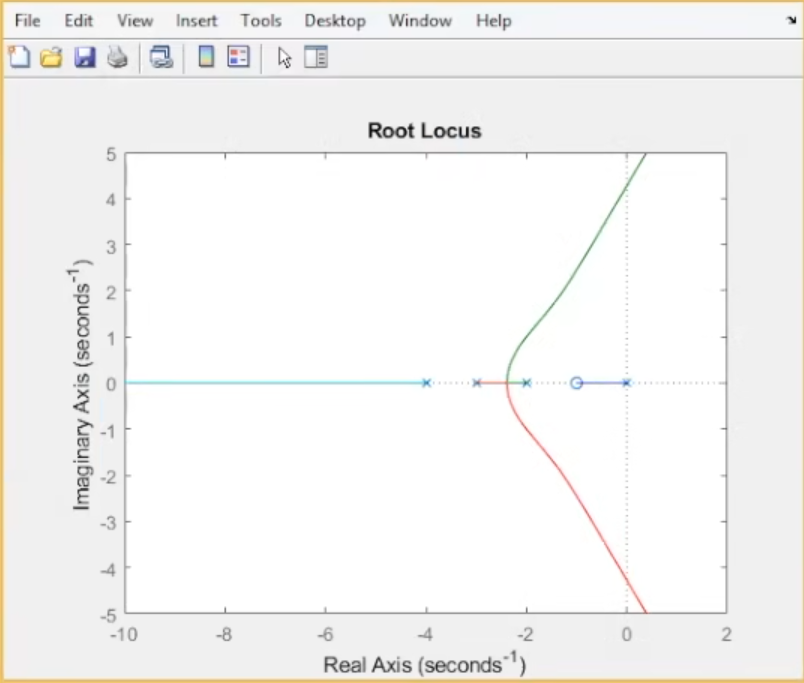
三、根轨迹——分离点/汇合点和根的性质
3.1 分离点/汇合点
在根轨迹分析中,分离点和汇合点是非常重要的概念,它们帮助我们理解系统极点在根轨迹中的行为。下面我将用通俗的语言解释这两个概念,并给出一些例子。
1. 分离点(Departure Point)
分离点是指根轨迹从一个极点开始离开的点。通常情况下,根轨迹从系统的极点出发,向外延伸。分离点的特征是:
- 极点:根轨迹的分离点总是系统的极点。
- 方向:根轨迹从分离点出发,可能会朝向零点、无穷远或其他极点。
例子:
假设我们有一个简单的传递函数:
G(s)=K(s+1)(s+2)
在这个例子中,系统有两个极点:s=−1 和 s=−2。当我们增加增益 K 时,根轨迹将从这两个极点出发,分别是它们的分离点。2. 汇合点(Arrival Point)
汇合点是指根轨迹到达的点。汇合点可以是系统的零点、无穷远或其他极点。汇合点的特征是:
- 零点:如果系统有零点,根轨迹可能会汇合到这些零点。
- 无穷远:如果没有零点,根轨迹可能会朝向无穷远延伸。
- 极点:根轨迹也可以在不同的极点之间汇合。
例子:
继续使用上面的传递函数:
G(s)=K(s+1)(s+2)
在这个例子中,由于没有零点,根轨迹将从极点 s=−1 和 s=−2 出发,最终朝向无穷远。因此,无穷远就是根轨迹的汇合点。3. 分离点和汇合点的图示
在根轨迹图中,分离点和汇合点可以通过以下方式表示:
- 分离点:在极点的位置标记为“×”,并从该点绘制出根轨迹。
- 汇合点:如果有零点,则在零点位置标记为“○”,并绘制根轨迹到达该点。如果没有零点,则根轨迹将朝向无穷远。
4. 例子总结
假设我们有一个系统的传递函数:
G(s)=K(s+1)(s+2)(s+3)
- 极点:s=−1、s=−2、s=−3
- 零点:假设没有零点。
在这种情况下:
- 分离点是 s=−1、s=−2、s=−3。
- 汇合点是无穷远。
5. 重要性
理解分离点和汇合点对于设计和分析控制系统至关重要。它们帮助我们预测系统的动态响应,确保系统在不同增益下的稳定性和性能。
先看一个典型二阶系统
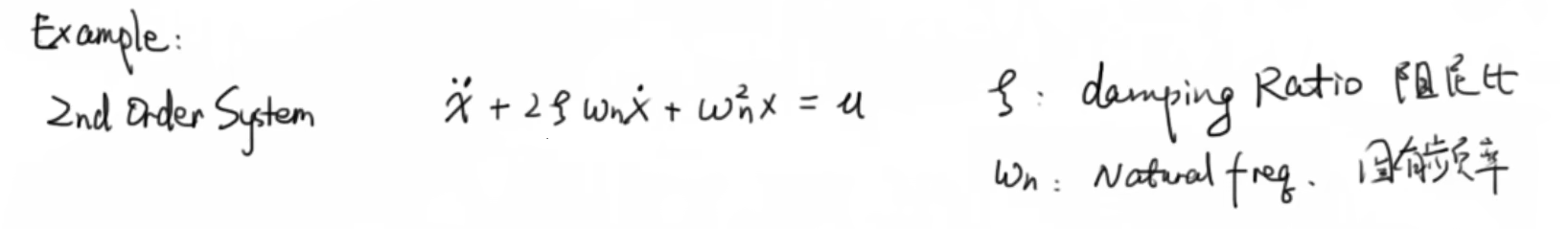
下面我们尝试用根轨迹的方法设计阻尼比
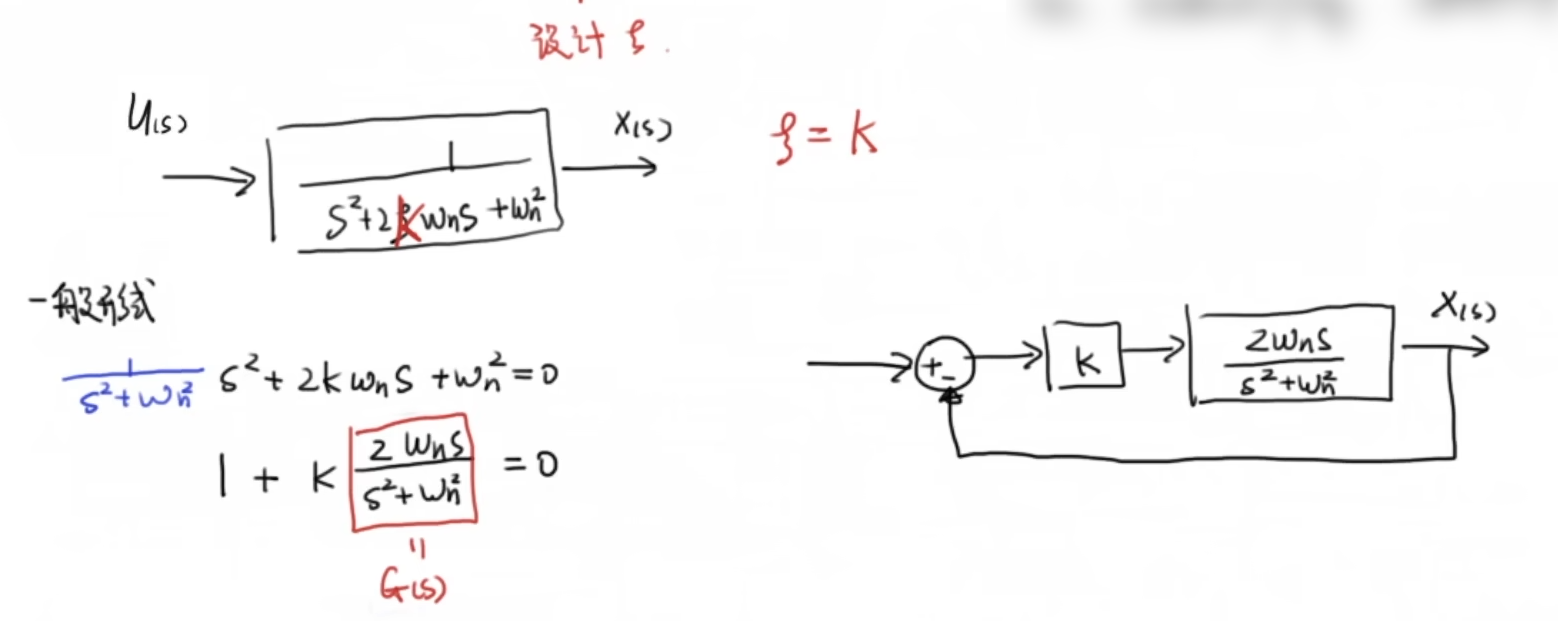
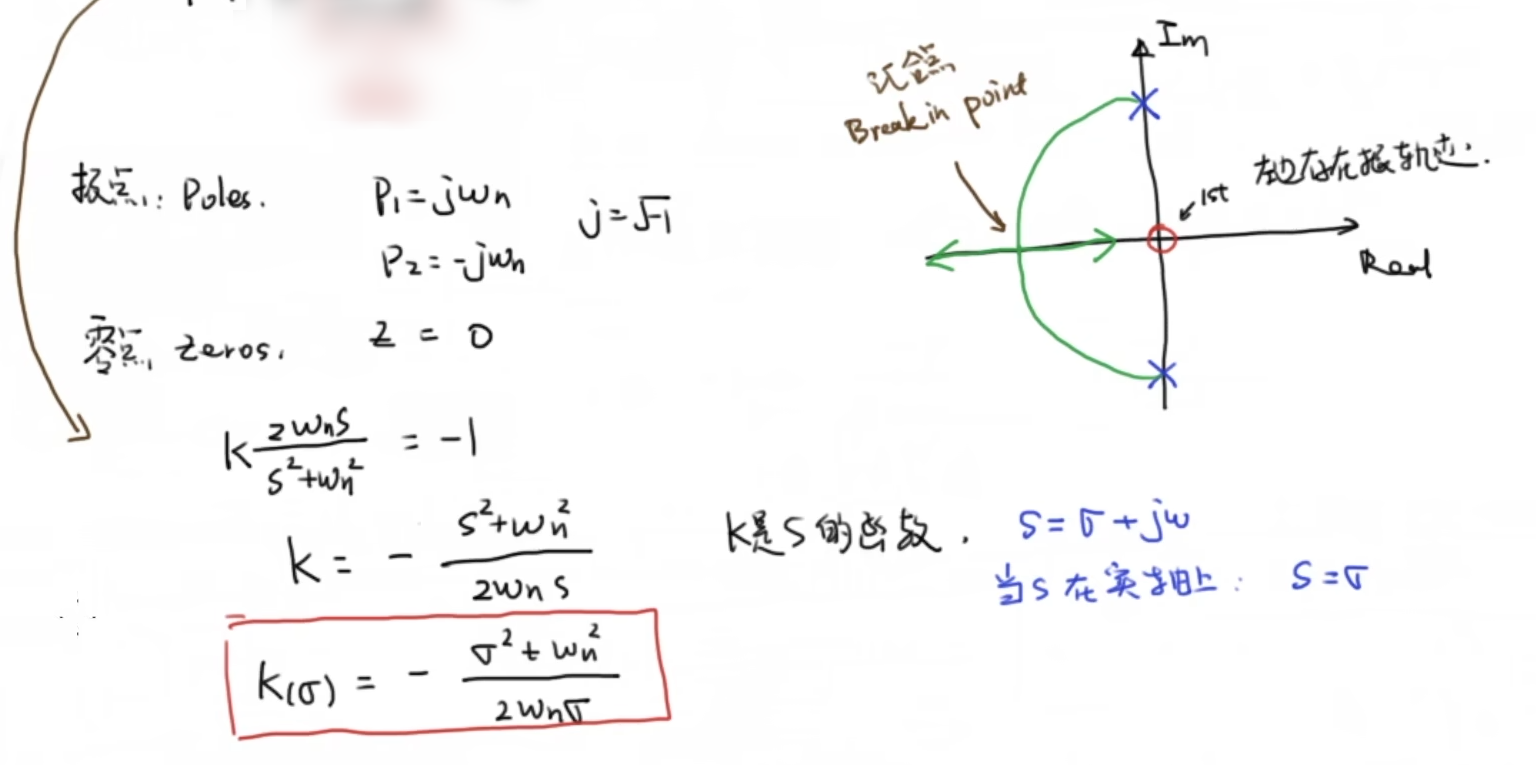

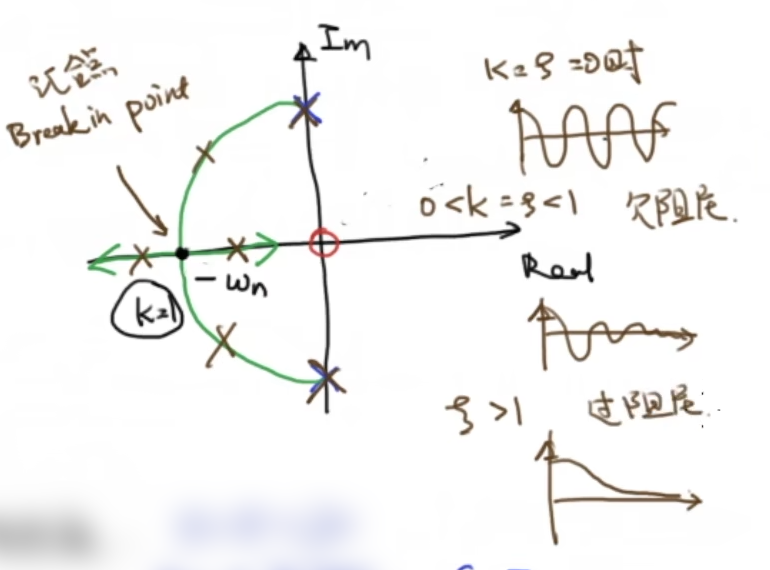
3.2 根轨迹重要的几何性质
学习根轨迹重要的几何性质可以为后面设计系统的控制器或者补偿器打下重要基础。
先来回顾一下复数的性质:

对于一个传递函数G(s)来说,如果我们把一个复数s = 6 + jw 代入
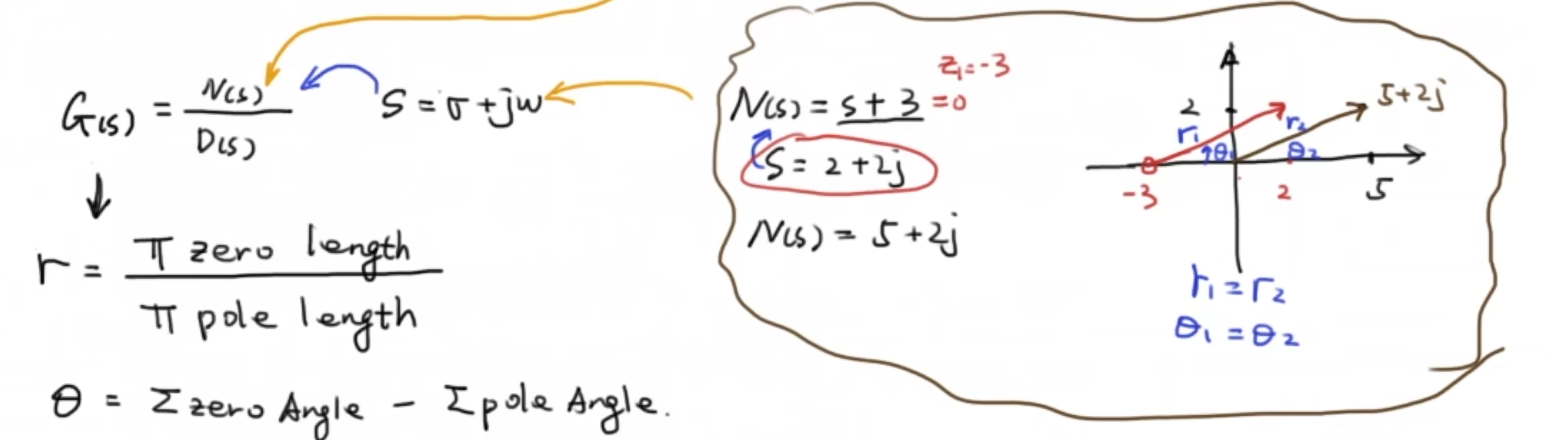
模长=所有零点到复数的距离的积 / 所以极点到复数距离的积
夹角=所有零点到复数夹角的和 - 所以极点到复数夹角的和
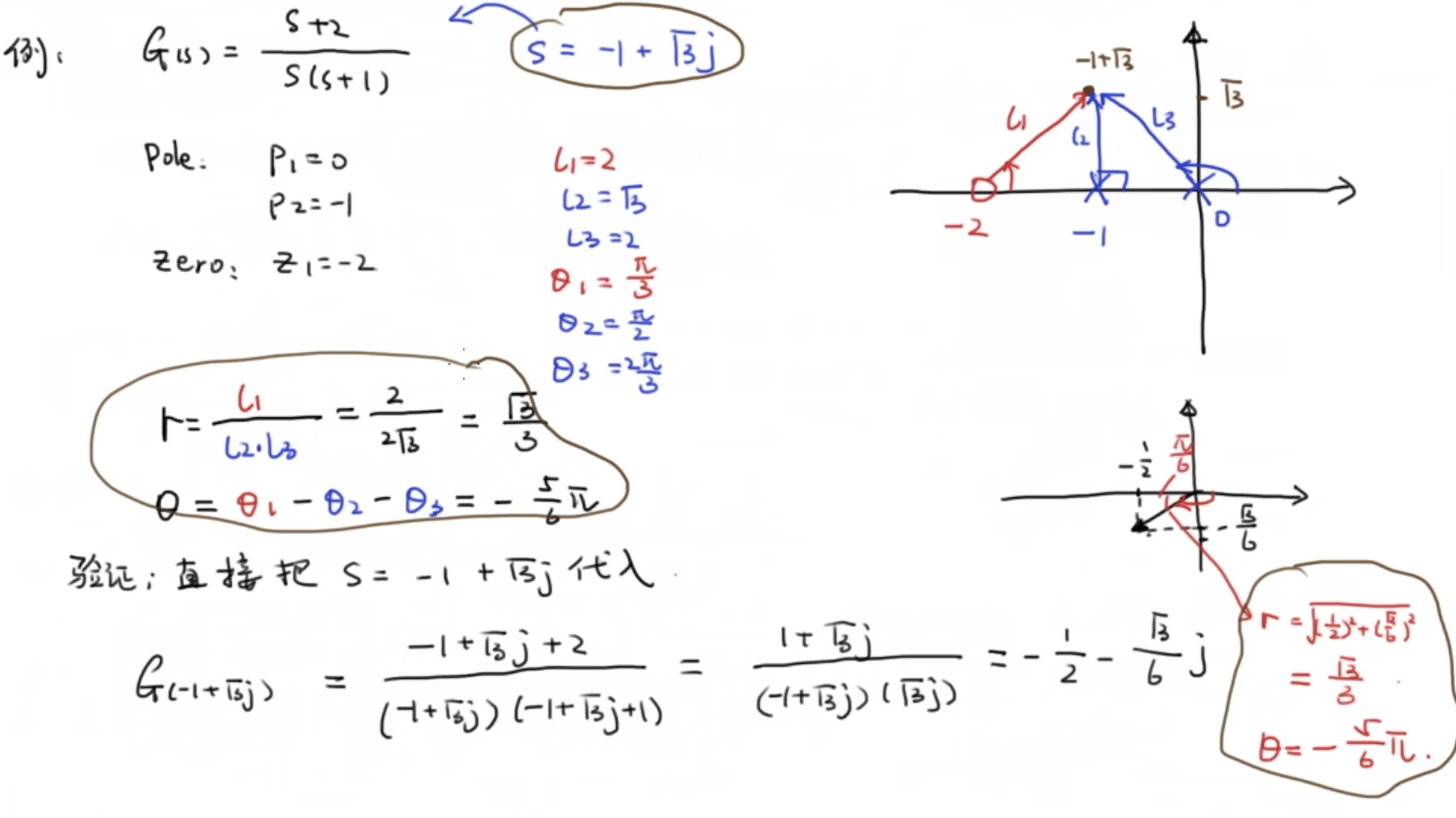
那这种通过几何方法求结果有什么用呢?其实这种便捷的方法可以为后续设计控制器打下基础,先看一下根轨迹的标准形式:
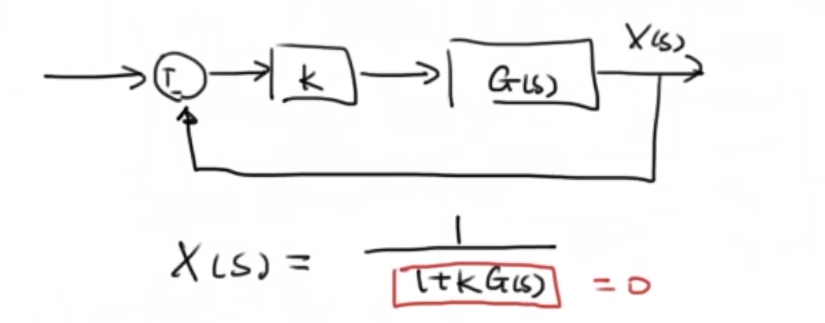

表示成 “所有零点到复数的距离的积 / 所以极点到复数距离的积”这种形式,就可以帮助我们判断一个根是否在根轨迹上。
总结
提示:这里对文章进行总结:
以上就是今天要学习的关于根轨迹的内容。





















 3933
3933

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








