本文介绍了在PyBullet环境中用GGCNN实现机械臂视觉抓取时，如何理解和处理相机内参与外参。文章强调了从2D像素点到3D世界坐标转换的重要性，并通过针孔相机模型解释了内参矩阵的作用，包括焦距、轴偏移和skew参数。此外，还提到了外参矩阵作为相机到世界坐标系转换的关键。在真实摄像头应用中，需要通过标定得到这些参数。
Auther：SeaHIRobot
date: 2023-05-03
最近在做一门课程的项目，在pybullet中复现GGCNN的机械臂视觉抓取的深度学习网络。在搭建仿真环境时，又回到了绕不开的相机内参和外参。借此机会对相机内参外参这一套进行一个review，对这个问题进行一个逻辑梳理。
因此本文不建议纯小白阅读，很多基础概念不会细讲，适合对相机内参外参有一定了解但不完全熟练的同学。
下面的链接是来自pybullet官方Doc中对相机内参的推荐阅读，讲的非常生动。
Dissecting the Camera Matrix, Part 3: The Intrinsic Matrix ←
这里的知乎文章也推荐阅读，内容详细：
Problem Defination - 问题定义
我们为什么要研究内参外参呢？这些东西有什么意义呢？
思考一下你目前想干的事情，你有一个相机，你想通过相机来提取场景信息，而通过相机你能获得到的仅仅是由rgb像素构成的2d画面。从3d的世界中，映射出一个2d的画面，这是相机的功能。你想做的，是通过相机输出的2d画面，获取3d信息，那么这中间就存在着2d的像素空间和3d的真实空间的一个变换。
我们要做的恰恰是寻找这种变换的一种数学表达，借助相机2d的由像素构成的画面，完成我们提取场景信息的任务。
”图片里2d的像素点位 → \rightarrow → 3d的世界坐标系中的点位“
这个任务既有3d的坐标变换，又有像素的2d点位向实际的空间坐标之间的尺度变换，怎么进一步拆分好让我们理解呢？那就是一步一步来咯。
”2d像素点位 → \rightarrow → 3d相机坐标系点位 → \rightarrow → 3d世界坐标系点位“
到这里不熟悉相机坐标系和齐次变换的同学请自行上网百科学习。
Pinhole Camera - 针孔相机
为什么讲针孔相机？这个模型有什么用？
因为他是一个很好理解这个问题的简单的模型，你可以简单得认为所有相机都是这么成像的；
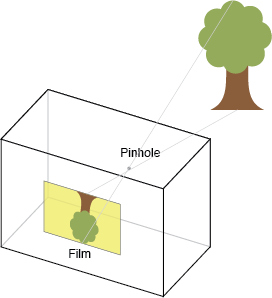
（图源http://ksimek.github.io/2013/08/13/intrinsic）
图中的box就是相机，小孔就是镜头。光路从环境中射入，通过小孔，最终在film上呈现倒像。倒像看起来比较烦，不如我们把按照相似三角形（或着说沿着Pinhole对称一下）到树的一边，就成了正像，如下图。（不用纠结这样做有什么意义，问就是方便看/doge，下面聊内参的时候你将会看到有了操作有多奇妙）
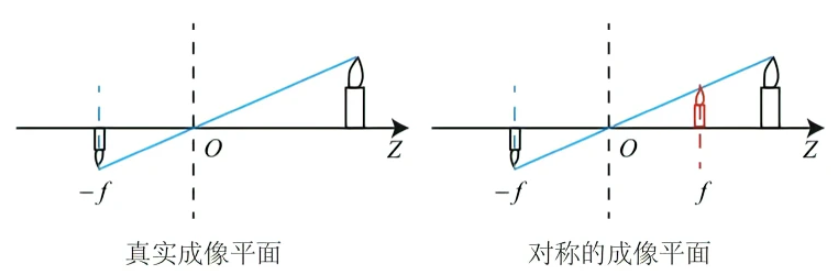
（图源https://zhuanlan.zhihu.com/p/389653208）
使用简单的相似三角形，貌似就可以解决针孔相机的问题。但如果事情再复杂一点呢？
比如：
- 被拍摄平面（图里的树）和film不是平行的
- film中心并不在Pinhole轴线上，有垂直轴线平面的偏移
- 实际的镜头有畸变，不符合针孔摄像头的简单的相似三角形变换
- blablabla…
下面就有请内参矩阵（intrinsic matrix）登场，进一步刻画这个问题。
Intrinsic Matrix - 内参矩阵
首先，内参矩阵长这个熊样子：
I
n
t
r
i
n
s
i
c
M
a
t
r
i
x
=
(
f
x
s
x
0
0
f
y
y
0
0
0
1
)
Intrinsic \ Matrix=\left(\begin{array}{c} f_x & s & x_0 \\ 0 & f_y & y_0 \\ 0 & 0 & 1 \end{array}\right)
Intrinsic Matrix=
fx00sfy0x0y01
先不纠结里面的参数，他干了一件什么事呢？见公式
(
u
v
1
)
=
1
z
c
(
f
x
s
x
0
0
f
y
y
0
0
0
1
)
(
x
c
y
c
z
c
)
\left(\begin{array}{c} u \\ v \\ 1 \end{array}\right) = \frac{1}{z_c}\left(\begin{array}{c} f_x & s & x_0 \\ 0 & f_y & y_0 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c} x_c \\ y_c \\ z_c \end{array}\right)
uv1
=zc1
fx00sfy0x0y01
xcyczc
它连接了像素平面的2d点相机系；
u和v指定了像素平面内的点位，脚标c代表了相机坐标系。 z c z_c zc是相机坐标系的z方向坐标，换一个说法，就是“深度”。前面的 1 z c \frac{1}{z_c} zc1也就是做z方向归一化，也可以把它写进后面的 ( x c , y c , z c ) T (x_c,y_c,z_c)^T (xc,yc,zc)T里，那么相机坐标系里的坐标就变成了在z方向归一化之后的坐标了。下面的图很好的阐释了这个过程，同时也解释了把真实像对称过来的妙处（因为看起来真的舒服）。
（自己画的，凑合看吧）
把上面的式子求个逆，就从像素坐标得到了在相机系中的坐标：
(
x
c
y
c
z
c
)
=
z
c
(
f
x
s
x
0
0
f
y
y
0
0
0
1
)
−
1
(
u
v
1
)
\left(\begin{array}{c}x_c \\ y_c \\ z_c \end{array}\right) = {z_c}\left(\begin{array}{c} f_x & s & x_0 \\ 0 & f_y & y_0 \\ 0 & 0 & 1 \end{array}\right)^{-1} \left(\begin{array}{c} u \\ v \\ 1 \end{array}\right)
xcyczc
=zc
fx00sfy0x0y01
−1
uv1
那 Intrinsic Matrix 里面的参数是干嘛的呢？？？为什么x和y方向都有一个焦距？？？s究竟是什么？？？ x 0 x_0 x0 y 0 y_0 y0到底用什么convention？？？
这里我简短回答一下:
- 有两个焦距的原因是实际传感器和理想模型的偏差，工艺、像素的几何形状等原因
- s s s描述了axis skew，传感器绕主轴的旋转程度，理想情况如仿真环境中，那 s s s就是0了（总不可能在相机组装的时候怼的准准的吧，不是吧不是吧）
- x o x_o xo y 0 y_0 y0描述了主轴偏移。因为z轴都归一化了，归一化的便利是可以用scaling的方式描述像素尺寸，那 x 0 x_0 x0 y 0 y_0 y0的单位顺理成章的也是像素了。因为我们描述图片的像素坐标时候，一般都是左上角为原点，x轴向右，y轴向下，在理想情况如仿真环境中，那 x 0 x_0 x0就是1/2的传感器宽度（像素值）， y 0 y_0 y0就是1/2的传感器高度（像素值）；当图片是640x480的时候， x 0 x_0 x0就是320， y 0 y_0 y0就是240。
详细的话还是参考http://ksimek.github.io/2013/08/13/intrinsic文章里的解释，作者还配上了交互式窗口，可以直观的感受内参矩阵的参数带来的影响（真的不是我懒，不是…）
Extrinsic Matrix - 外参矩阵
上面我们借助内参矩阵完成了像素点 ( u , v ) (u,v) (u,v)到对应的相机坐标系下的点 ( x c , y c , z c ) (x_c,y_c,z_c) (xc,yc,zc)，那么想要最重要获得 ( u , v ) (u,v) (u,v)对应的世界坐标系中的点，那还不好办，只需要知道变换矩阵 Transfer Matrix 就可以了。所以外参矩阵就是单纯的相机系到约定的世界坐标系的 4by4 的 齐次变换矩阵。
齐次变换掌握不牢固的自行补一补。
到这里，我们最后用公式梳理一下怎么从二维像素点位鼓捣到三维世界坐标点位的：
第一步：
(
x
c
y
c
z
c
)
=
z
c
(
f
x
s
x
0
0
f
y
y
0
0
0
1
)
−
1
(
u
v
1
)
第二步：
(
x
w
y
w
z
w
)
=
H
c
w
(
x
c
y
c
z
c
)
M
i
s
s
i
o
n
c
o
m
p
l
e
t
e
d
.
第一步：\left(\begin{array}{c}x_c \\ y_c \\ z_c \end{array}\right) = {z_c}\left(\begin{array}{c} f_x & s & x_0 \\ 0 & f_y & y_0 \\ 0 & 0 & 1 \end{array}\right)^{-1} \left(\begin{array}{c} u \\ v \\ 1 \end{array}\right) \\ \\ 第二步：\left(\begin{array}{c} x_w \\ y_w \\ z_w \end{array}\right) = H_{c}^{w}\left(\begin{array}{c} x_c \\ y_c \\ z_c \end{array}\right) \\ \\ Mission \ completed.
第一步：
xcyczc
=zc
fx00sfy0x0y01
−1
uv1
第二步：
xwywzw
=Hcw
xcyczc
Mission completed.
相机标定
在仿真环境中，是不用标定的，按照理想情况构造就行了。
使用真实摄像头就涉及到标定的环节，通过标定我们其实就是为了拟合出像模像样的Intrinsic Matrix和Extrinsic Matrix，好让我们完成这个从二维像素平面提取世界中的三维信息的任务。
完结
觉得有用点个赞
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
