扩展卡尔曼滤波器

概述

本文对上文的卡尔曼滤波知识进行些许补充，并简单说明扩展卡尔曼的知识及用法。

正文

对卡尔曼滤波的补充

卡尔曼是一种多数据递归融合算法，同时也可以理解为一个权重在变化的低通滤波器。

其思想公式为：

$当前的估计值=上一次估计值+权重\ast （当前测量值-上一次估计值）$

所以，递归次数越多，测量值的作用越小，其估计值越接近真实值。如下例子：

假设A的真实值为50，经过上述公式计算后，结果波形如下：

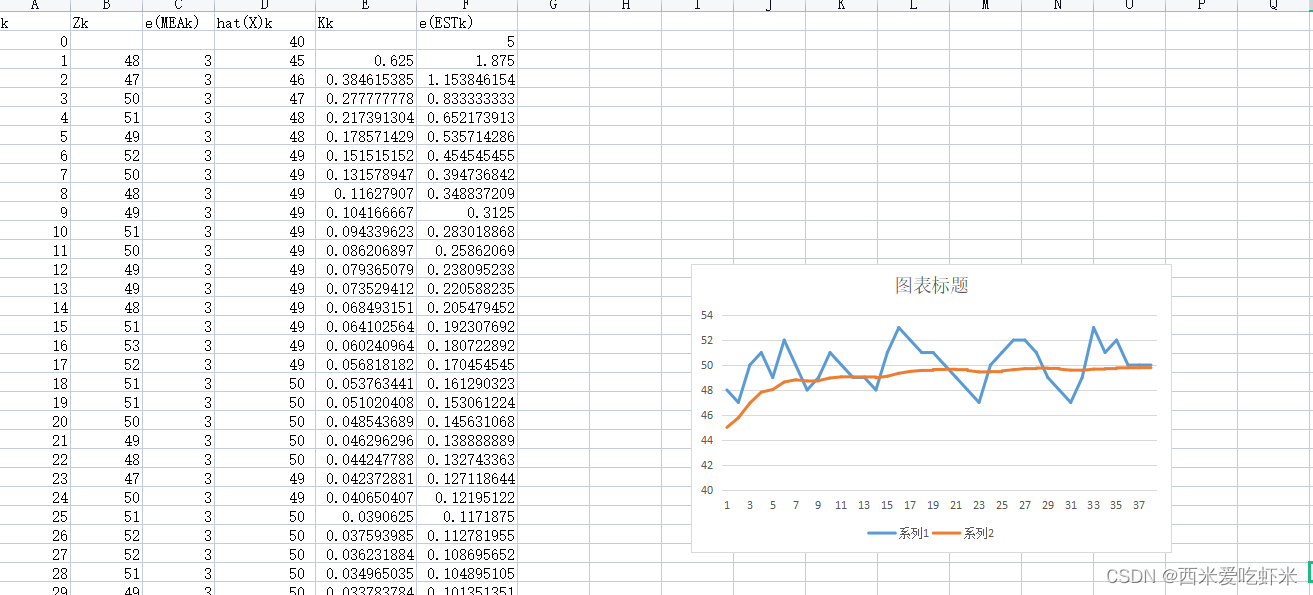
所谓的数据融合，其实就是通过计算增益值K使得测量值的方差$\Sigma$最小，使得数据为最优解。

使用卡尔曼滤波器的步骤：

(1)建立系统的状态空间方程和测量方程

例如：二维的位置P、速度V恒定速度系统，测量值为P，无控制量

$P_k=P_{k-1}+V_k\ast \Delta t+W_{p,k}$

$V_k=V_{k-1}+W_{v,k}$

$Z_{p,k}=X_{p,k}+V_{p,k}$

$Z_{v,k}=0$

$W$、$V$为过程噪声和测量噪声。

设状态向量$\widehat{X_k}={\left|\begin{array}{cc}{P}_k& V_k\end{array}\right|}^T$

所以用矩阵表示为：

$\left|\begin{array}{c}{P}_k\\ V_k\end{array}\right|=\left|\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right|\left|\begin{array}{c}{P}_{k-1}\\ V_{k-1}\end{array}\right|+\left|\begin{array}{cc}{Q}_p& 0\\ 0& Q_v\end{array}\right|\left|\begin{array}{c}{W}_{p,k}\\ W_{v,k}\end{array}\right|$

$Z_k=\left|\begin{array}{cc}1& 0\end{array}\right|\left|\begin{array}{c}{X}_{p,k-1}\\ X_{v,k-1}\end{array}\right|+\left|\begin{array}{cc}{R}_p& 0\end{array}\right|\left|\begin{array}{c}{V}_{p,k-1}\\ V_{v,k-1}\end{array}\right|$

(2)将矩阵代入公式计算

这里状态转移矩阵$F=\left|\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right|$

由于没有控制量，所以$B=0$

过程噪声协方差矩阵$Q$其实就是前面的$\left|\begin{array}{cc}{Q}_p& 0\\ 0& Q_v\end{array}\right|$

测量噪声协方差矩阵$R$其实就是前面的$\left|\begin{array}{cc}{R}_p& 0\end{array}\right|$

由于状态协方差矩阵只在初始阶段产生影响，且位置速度噪声相互独立，所以一般可以给定矩阵初始值$P_0=\left|\begin{array}{cc}\sigma {{}_p}^2& \sigma {}_p\sigma {}_v\\ \sigma {}_v\sigma p& \sigma {{}_v}^2\end{array}\right|=\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|$

系统转换矩阵$H=\left|\begin{array}{cc}1& 0\end{array}\right|$

扩展卡尔曼滤波器

扩展卡尔曼应用于非线性程度不高的系统。扩展卡尔曼其实与卡尔曼很类似，只是扩展卡尔曼是利用泰勒级数展开对$k-1$时刻求$f(x)$对$x$的偏导。所以两者最大的区别是状态转移矩阵$F$和系统转换矩阵$H$用雅各比矩阵表示。

即扩展卡尔曼先验估算公式为：

${\hat{X}}_k=f({\hat{x}}_{k-1},{\hat{u}}_{k-1},0)$

后验估算公式为：

${\hat{X}}_k^{\prime }={\hat{X}}_k+K(Z_k-h({\hat{X}}_k))$

例如：

某系统的状态空间方程为：

$X_1=X_1+SIN(X_2)=f_1(x)$

$X_2=X_1^2=f_2(x)$

$Z_1=\frac{1}{2}COS(X_1)=h_1(x)$

$Z_2=0=h_2(x)$

所以：

$F={\left|\begin{array}{cc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ & \\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\end{array}\right|}_{x_{1k-1},x_{2k-1}}=\left|\begin{array}{cc}1& cos(x_{2k-1})\\ 2x_{1k-1}& 0\end{array}\right|$

$H={\left|\begin{array}{cc}\frac{\partial h_1}{\partial x_1}& \frac{\partial h_1}{\partial x_2}\\ & \\ \frac{\partial h_2}{\partial x_1}& \frac{\partial h_2}{\partial x_2}\end{array}\right|}_{x_{1k-1},x_{2k-1}}=\left|\begin{array}{cc}-\frac{1}{2}sin(x_{1k-1})& 0\end{array}\right|$

由此可以看出$F$、$H$随着$k$的变化而变化。

其余公式与卡尔曼滤波公式一致，将这两个雅各比矩阵代入重新计算即可。

总结

如上所说，即可完成将卡尔曼滤波器改写成扩展卡尔曼滤波器。