滑动窗口

题目描述

给定一个长度为 n 的数列。
有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子：
该数组为 [2 4 -1 -2 6 2 7 8 4]，k 为 4。

窗口位置	最小值	最大值
[2 4 -1 -2] 6 2 7 8 4	-2	4
2 [4 -1 -2 6] 2 7 8 4	-2	6
2 4 [-1 -2 6 2] 7 8 4	-2	6
2 4 -1 [-2 6 2 7] 8 4	-2	7
2 4 -1 -2 [6 2 7 8] 4	2	8
2 4 -1 -2 6 [2 7 8 4]	2	8

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入描述

输入包含两行。
第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数，代表数组的具体数值。
同行数据之间用空格隔开。

输出描述

输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。

样例输入

8 3
1 3 -1 -3 5 3 6 7

样例输出

-1 -3 -3 -3 3 3
3 3 5 5 6 7
这道题就是经典的单调队列

单调队列就是维护一个队列,保持队列的单调递增/递减性

单调队列的模拟过程如下

比如我们有1 4 5 3要插入下面的单调递增队列中

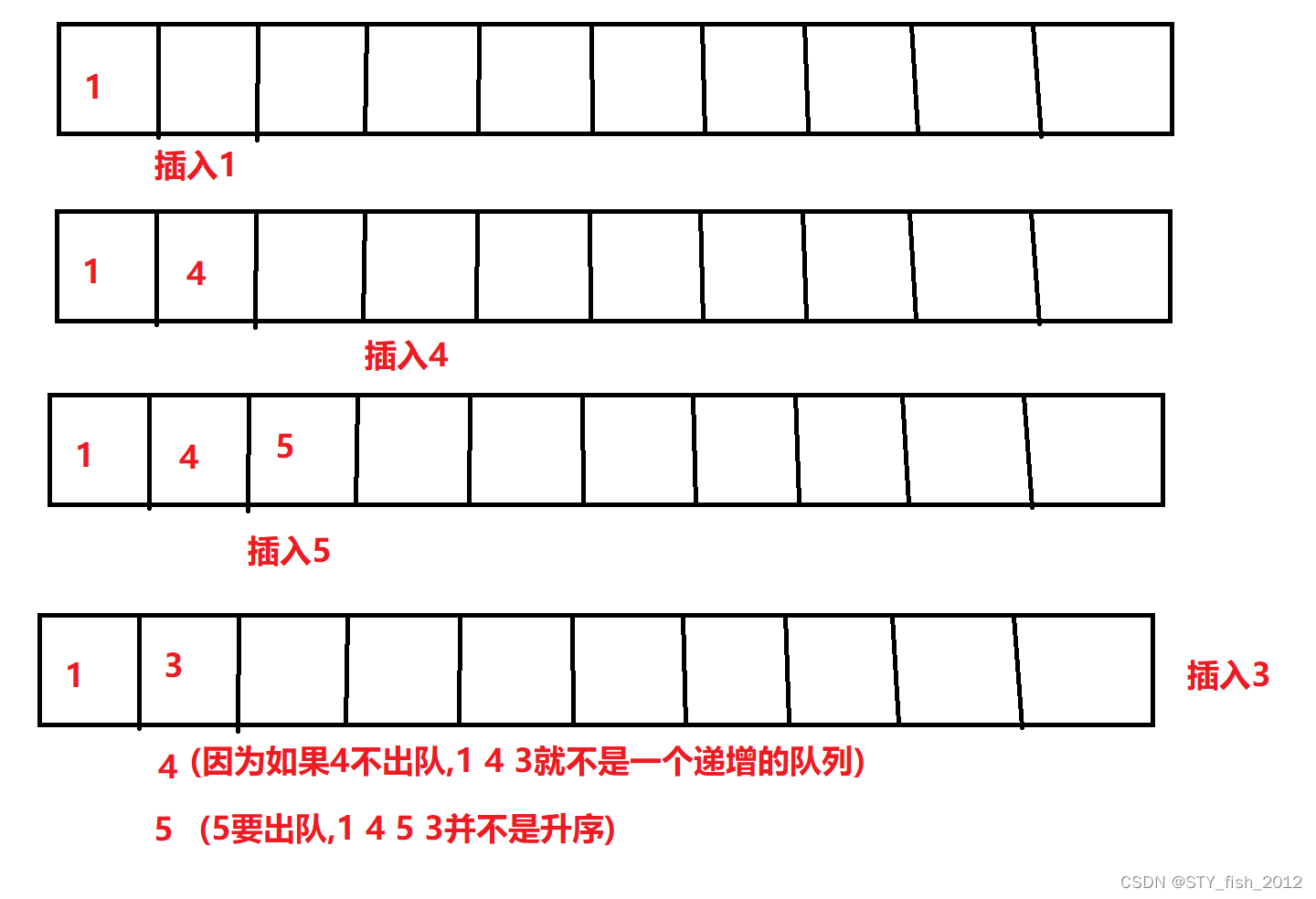
单调队列就是要在元素入队时比较一下这个元素与队头,如果插入此元素是队列失去了升序,就将目前队头出队,直到插入元素为升序,就插入

回到这道题,那么我们就要建立两个队列 q_min 和 q_max,来完成区间最大值和区间最小只的输出

先来看一下最小值

那么我们就需要一个单调递增队列来完成

我们要保持队头始终是区间内的最小值(保持队列单调性),就得在元素入队时加上一个while循环,如果a[i] (a[i]指入队元素) 比队尾小,就破坏了队列的单调性,但是a[i]必须入队,就要把队尾元素删除,直到队列里的元素都被他挤了出去或是找到了合适的位置(a[i]>=了队头)为止

while(head<=tail&&num[q_min[tail]]>num[i])tail--;

接着,下面要做一个判断,就是如果入队的元素已经达到了m个,就要进行输出了,但对于大于m个元素了,就要再写一个while循环,维护区间长度只有m个

while(head<tail&&i-q_min[head]>=k)head++;

最后再输出一下队头,最小值就完成了

最大值的思路和最小值一样,但是入队时的操作有一点小小的改动

while(head<=tail&&num[q_max[tail]]<num[i])tail--;

完整代码如下:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,k;
int num[N];
int q_min[N];
int q_max[N];
int head,tail;
int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		cin>>num[i];
	for(int i=1;i<=n;i++){
		while(head<=tail&&num[q_min[tail]]>num[i])tail--;
		q_min[++tail]=i;
		if(i>=k){
			while(head<tail&&i-q_min[head]>=k)head++;
			cout<<num[q_min[head]]<<" ";
		}
	}
	cout<<endl;
	for(int i=1;i<=n;i++){
		while(head<=tail&&num[q_max[tail]]<num[i])tail--;
		q_max[++tail]=i;
		if(i>=k){
			while(head<tail&&i-q_max[head]>=k)head++;
			cout<<num[q_max[head]]<<" ";
		}
	}
	return 0;
}