【ybt】【基算二分课过例2】防具布置

最新推荐文章于 2022-10-24 20:11:57 发布

原创最新推荐文章于 2022-10-24 20:11:57 发布 · 169 阅读

0 ·

CC 4.0 BY-SA版权

ybt 同时被 2 个专栏收录

91 篇文章

订阅专栏

二分

3 篇文章

订阅专栏

博客围绕防具布置问题展开，先指出每个点及之前点的防具数量可在 O(n) 时间复杂度求出，接着说明因只有一处防线有问题，若当前点为奇数，有问题的防线在其之前，可据此进行二分查找，时间复杂度为 O(logn)，还提到若第 2147483647 道防线为偶数则无问题。

防具布置

题目链接：防具布置

题目描述

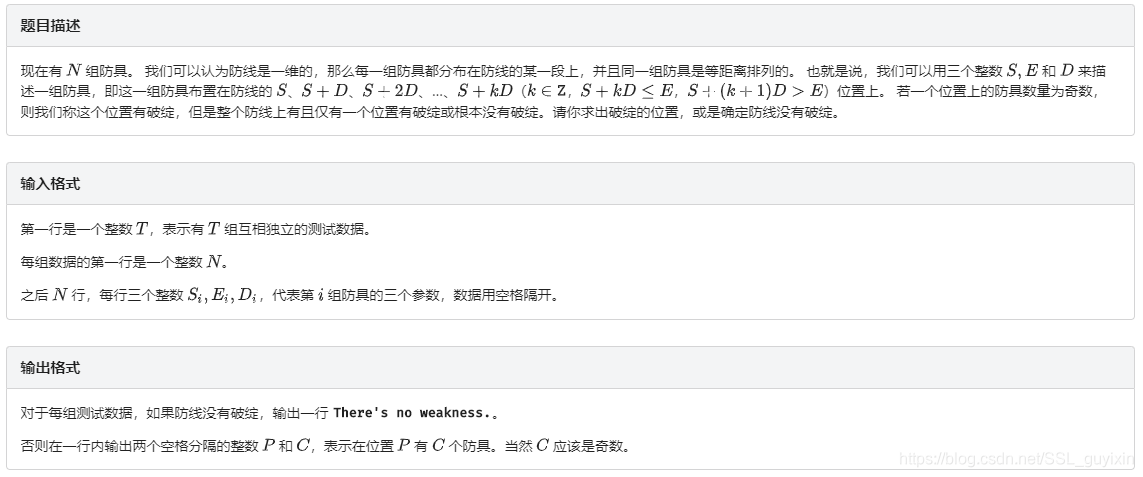
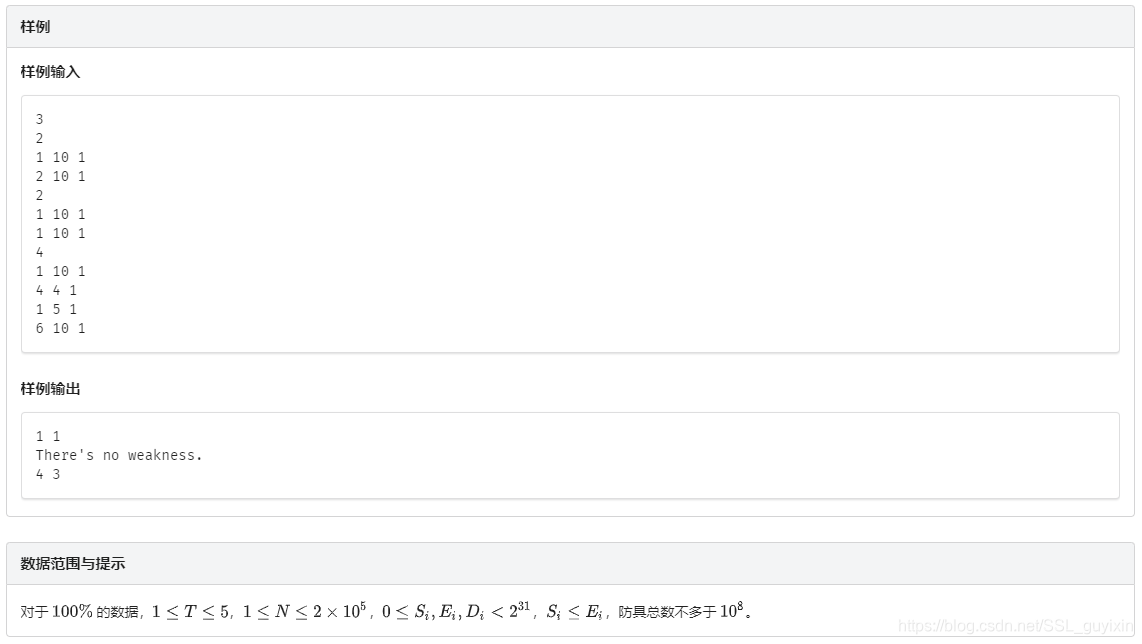
在这里插入图片描述

解题思路

首先，每个点及之前的点一共有多少个防具是可以求出来的， $O (n)$ 。

然后，因为只有一处防线有问题，所以如果当前点为奇数，那么有问题的防线一定是在它之前的，我们就可以以此为基础进行二分。 $O(\log{n})$ 。

当然，如果第 $2147483647$ 道防线是偶数，那么全部的防线都没有问题了。

code

#include<iostream>
#include<cstdio>
#define int long long
using namespace std;

int T;
int n;
int s[200010],e[200010],d[200010];

int check(int t)
{
	int ans=0;
	for(int i=1;i<=n;i++)
		if(s[i]<=t)
			ans+=(min(e[i],t)-s[i])/d[i]+1;
	return ans;
}

void work()
{
	if(check(2147483647)%2==0)
	{
		printf("There's no weakness.\n");
		return; 
	}
	int l=0,r=2147483647;
	while(l<r)
	{
		int mid=(l+r)/2;
		if(check(mid)%2==1)
			r=mid;
		else
			l=mid+1;
	}
	cout<<l<<" "<<check(l)-check(l-1)<<endl;
}

signed main()
{
	cin>>T;
	while(T--)
	{
		cin>>n;
		for(int i=1;i<=n;i++)
			scanf("%lld%lld%lld",&s[i],&e[i],&d[i]);
		work();
	}
}