【ybt】【基算 二分 课过 例3】最大均值

最大均值

题目链接：最大均值

---

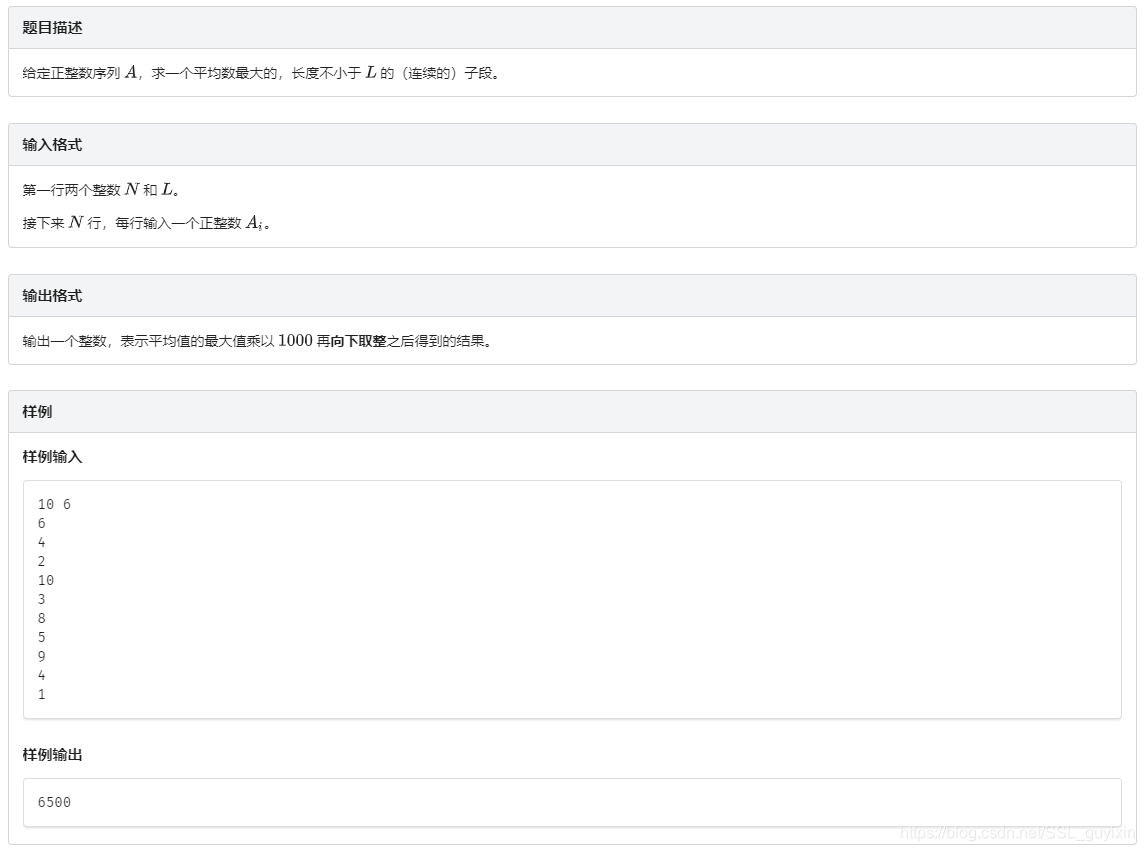
题目描述

解题思路

很明显是二分平均值。

这样就用掉了 $O(\log n)$ 的时间复杂度，而一般的二分题是 $O(n\log n)$ 的时间复杂度（也可能是我才疏学浅没有遇到过难一点的）。

现在问题就变成了：如何用 $O(n)$ 的时间复杂度验证在平均值为 $mid$ 的情况下序列中是否存在一个长度大于 $l$ 的。

平均值大于 $mid$ ，换句话来说就是序列中所有数减去 $mid$ 后总和大于 $0$ 。

再想想如何 $O(1)$ 求一个序列的总和（预处理之后），我们很显然可以想到前缀和。

前缀和，无非就是后面减前面。那么如果在枚举时从前往后枚举，只需要找前面最小的和后面的相减，长度大于 $l$ 即可。若如上操作得到的最大差值大于 $0$ ，那么这个序列中就存在一个子序列平均值大于 $mid$ 。

code

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

int n,L;
double a[100010];
double b[100010];

int check(double k)
{
	for(int i=1;i<=n;i++)
		b[i]=b[i-1]+a[i]-k;
	double minn=2000,ans=-2000;
	for(int i=L;i<=n;i++)
	{
		minn=min(minn,b[i-L]);
		ans=max(ans,b[i]-minn);
	}
	return ans>=0;
}

int main()
{
	cin>>n>>L;
	for(int i=1;i<=n;i++)
		scanf("%lf",&a[i]);
	double l=-2000,r=2000;
	while(l+0.00001<r)
	{
		double mid=(l+r)/2;
		if(!check(mid))
			r=mid;
		else
			l=mid;
	}
	cout<<(int)(floor(r*1000))<<endl;
}