VAR模型分析全流程详解：从理论到实践

一、VAR模型简介与SPSSAU优势

向量自回归(VAR)模型是一种广泛应用于多变量时间序列分析的计量经济学方法。与传统单方程模型不同，VAR模型将系统中所有变量都视为内生变量，通过联立方程的形式捕捉变量间的动态交互关系。这种方法的优势在于不需要预先设定理论假设，让数据自身说话，特别适合分析经济、金融等复杂系统中的相互影响机制。

SPSSAU作为一款智能统计分析平台，在VAR模型分析上实现了流程化、自动化的操作体验。用户无需编写复杂代码，通过界面点选即可完成从模型设定到结果解读的全过程，大大降低了多变量时间序列分析的技术门槛。

二、VAR模型分析全流程

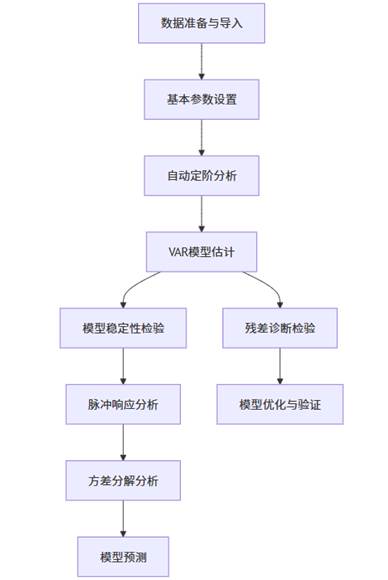
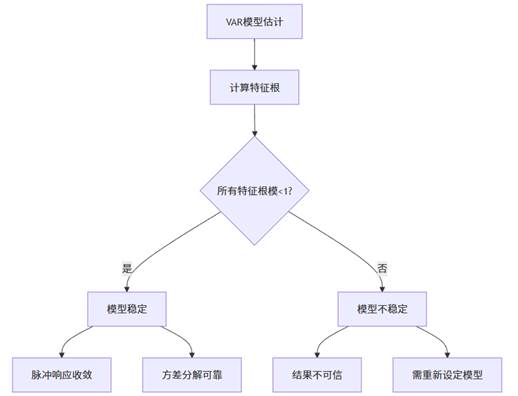
上图展示了SPSSAU中进行VAR模型分析的完整流程。这一流程遵循从模型设定到结果应用的逻辑顺序，确保每个环节都建立在前面分析的基础上。SPSSAU的智能化体现在：系统会自动完成技术性较强的步骤（如滞后阶数选择），同时为用户提供专业的解读指南，即使是初学者也能顺利完成复杂的多变量时间序列分析。

SPSSAU进行VAR模型分析操作示例如下：

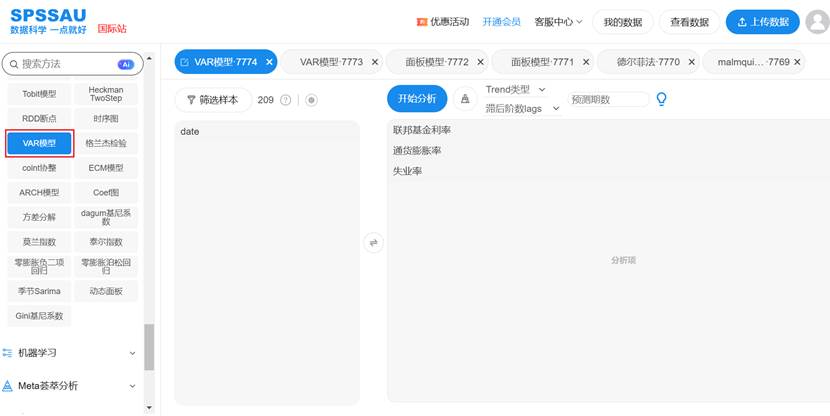
三、核心参数设置与理论基础

3.1 趋势类型选择

在VAR模型中，趋势类型的设定关系到变量长期行为的假设。SPSSAU提供三种主要选择：

• 无趋势（None）：假设时间序列不存在确定性趋势，适合平稳性较强的数据
• 常数项（Constant）：允许序列有非零均值，但增长率为零，是最常用的选择
• 线性趋势（Linear Trend）：假设序列存在稳定的线性增长趋势

理论指导：趋势类型的选择应结合经济理论和数据特征。当不确定时，可从常数项开始，通过信息准则比较不同趋势类型的模型优劣。

3.2 滞后阶数确定

滞后阶数决定变量过去值对当前值的影响时长，是VAR模型的核心参数之一。SPSSAU采用多准则自动定阶方法，平衡模型的简洁性与拟合优度。

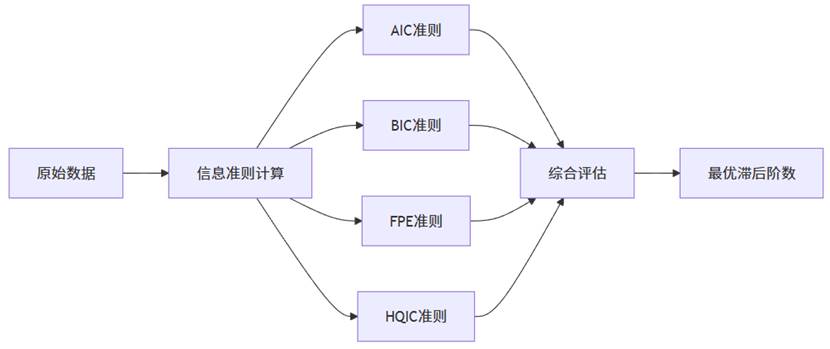
滞后阶数选择涉及过拟合与欠拟合的权衡：阶数过低会遗漏重要动态关系，阶数过高则会增加估计不确定性并降低预测精度。SPSSAU同时计算四种信息准则，为用户提供全面参考，最终基于多数原则确定最优滞后阶数。分析结果示例如下：

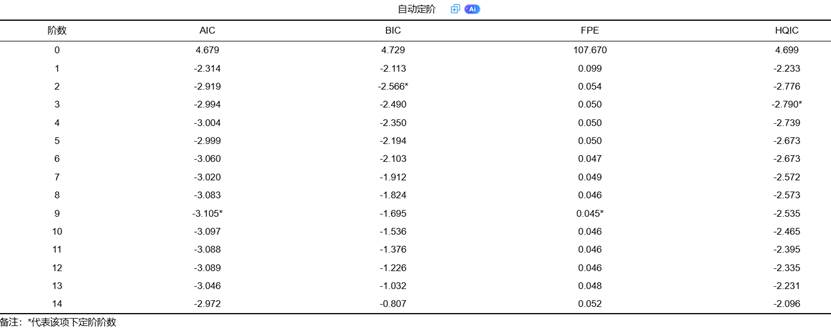
四、VAR模型结果解读

SPSSAU输出VAR模型分析结果示例如下：

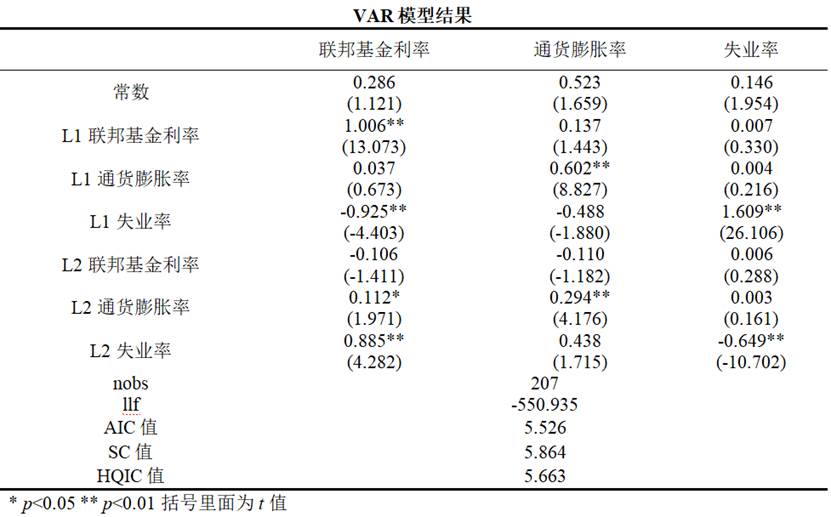
4.1 模型系数与统计显著性

VAR模型结果表格展示了各变量及其滞后项之间的动态关系。解读要点包括：

• 系数符号与大小：反映影响的方向和强度
• t统计量与p值：判断关系是否 statistically significant
• 星号标记系统：直观显示显著性水平（*p<0.05, **p<0.01）

需要强调的是，VAR模型中单个系数的经济解释较为困难，不应过度解读。模型的真正价值在于整体动态关系的刻画，而非单个参数的意义。

4.2 模型整体评价指标

• AIC（Akaike信息准则）：平衡模型拟合优度与复杂性，越小越好
• SC/BIC（贝叶斯信息准则）：对参数化更加谨慎，惩罚项比AIC更大
• HQIC（Hannan-Quinn准则）：介于AIC与BIC之间的折中准则

这些指标不仅用于评价单个模型的质量，更重要的是比较不同设定下模型的相对优劣。SPSSAU同时提供这三个指标，为用户提供全面的模型评价依据。

五、模型诊断与稳定性分析

5.1 AR根图与模型稳定性

VAR模型稳定的充要条件是所有特征根的模都小于1，即位于单位圆内。SPSSAU通过AR根图直观展示这一条件：

稳定性是VAR模型有效的前提。不稳定的模型会导致脉冲响应不收敛、方差分解无意义，预测结果偏离实际。SPSSAU自动生成AR根图，并给出明确的稳定性判断，确保后续分析建立在可靠基础上。

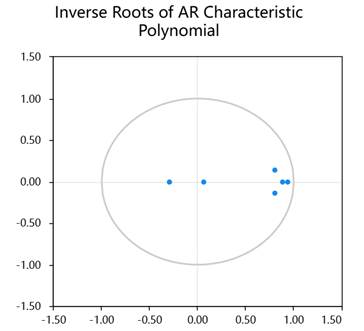
从AR特征根图可知，所有特征根值均在单位圆之内，意味着构建的VAR模型稳定性较好。

5.2 残差诊断检验

残差诊断是验证模型设定正确性的关键步骤，包括残差正态性检验和自相关检验：

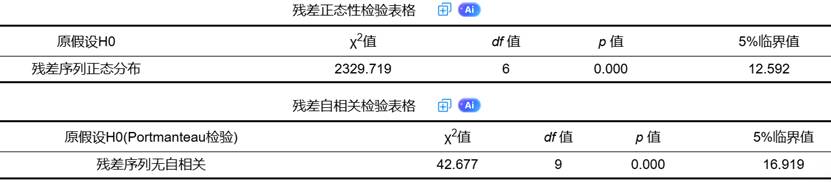
（1）正态性检验：

• 原假设：残差服从多元正态分布
• 检验意义：满足正态性假设时，统计推断更加可靠
• SPSSAU实现：基于Jarque-Bera方法的多元扩展

（2）自相关检验：

• 原假设：残差无自相关
• 检验意义：自相关存在说明模型未充分捕捉动态关系
• SPSSAU实现：Portmanteau检验（也称作Q检验）

残差诊断不通过时，提示模型可能需要：增加滞后阶数、引入趋势项、考虑变量变换，或者改用更复杂的VECM模型。SPSSAU会明确标识检验结果，并给出相应的处理建议。

六、动态分析工具

6.1 脉冲响应函数（IRF）

脉冲响应函数描述系统对一个变量"意外冲击"的动态反应路径，是VAR模型最有力的分析工具之一。

理论核心：

• 正交化脉冲响应：通过Cholesky分解消除变量间同期相关性
• 响应持续时间：冲击影响逐渐衰减的过程
• 响应方向与强度：正负号表示作用方向，绝对值表示影响程度

SPSSAU提供可视化脉冲响应图和数值表格两种形式，支持用户从不同角度理解变量间的动态互动。结果示例如下：

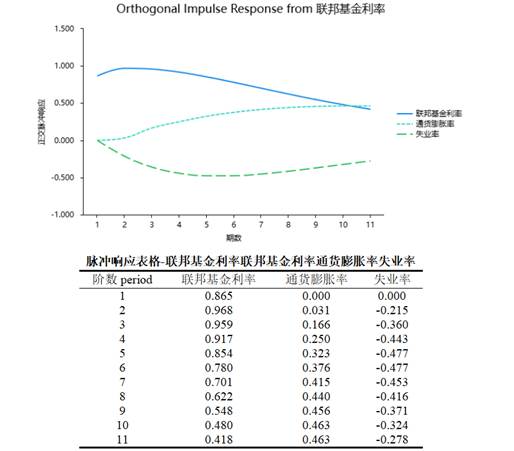
通过观察脉冲响应，可以回答诸如"货币政策冲击对产出的影响持续多久"、"价格冲击如何随时间传播"等重要经济问题。

6.2 方差分解（FEVD）

方差分解将预测误差方差按成因分解，量化各变量的相对重要性：

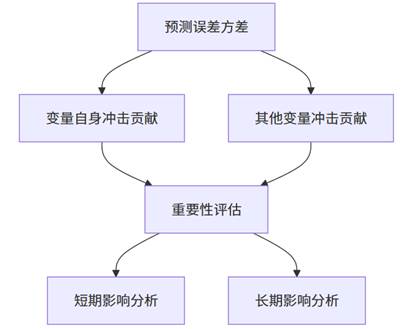
方差分解的核心价值在于：

• 识别主导力量：找出对系统波动影响最大的变量
• 分析动态演变：观察各变量重要性随时间的变化
• 验证经济理论：与理论预期对比，评估模型合理性

SPSSAU的方差分解结果以百分比形式呈现，直观展示各变量的贡献度，且支持多期比较，帮助用户全面把握系统的波动源泉。结果示例如下：

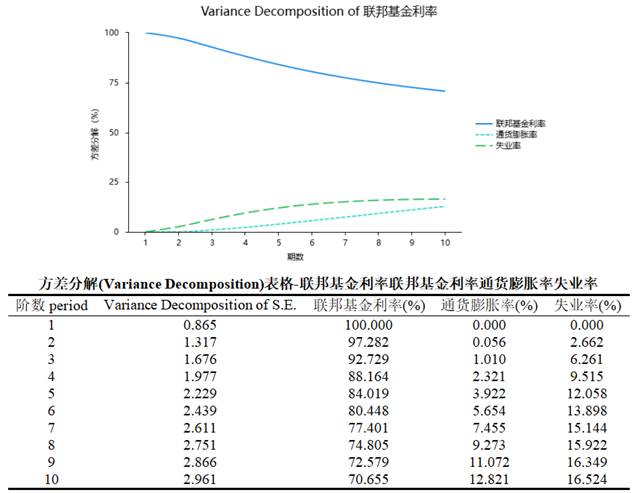
七、预测与应用

VAR模型在政策分析、经济预测、风险评估等领域有广泛应用。SPSSAU提供灵活的预测功能：

• 预测期数自定义：满足不同需求的时间跨度
• 多变量同步预测：保持变量间的内在联系
• 预测结果可视化：直观展示未来走势

预测本质上是基于历史规律和当前关系的条件外推，其准确性依赖于模型设定的正确性和结构稳定性的维持。SPSSAU不仅提供点预测，还通过多种方式评估预测不确定性，帮助用户理性使用预测结果。

八、结语

VAR模型作为多变量时间分析的重要工具，其价值已在学术研究和实际应用中得到充分验证。SPSSAU通过流程化设计、智能化处理、可视化展示，让这一强大方法变得更加亲民易用。

无论是宏观经济研究、金融市场分析，还是商业决策支持，SPSSAU的VAR分析功能都能提供专业、可靠的技术支撑。平台兼顾了方法的严谨性与操作的便捷性，既保证结果的可信度，又降低使用的技术门槛。