ROC曲线分析：从医学诊断到模型评估的完整指南

在评估一个分类器或诊断工具的效能时，一个核心问题是：它能否准确地区分不同类别？无论是医学上区分患者与健康人，金融风控中识别欺诈交易，还是机器学习模型进行图像分类，我们都需要一个超越简单“准确率”的、更稳健的性能评估框架。ROC曲线分析正是应对这一需求的强大工具。

ROC曲线的历史颇具传奇色彩。它起源于二战期间，用于分析雷达信号接收器区分真实信号（敌机）与噪声（环境干扰）的性能，故而得名“接收者操作特征曲线”。20世纪60年代，这一方法被引入到心理学领域，用于研究感知觉的辨别力。直到70年代末，它才在医学诊断试验评价中扎根并大放异彩，成为评价和比较诊断方法的金标准。

本文将系统性地剖析ROC分析的理论基础、核心指标、解读方法及其在现代数据分析中的多元化应用。

一、 诊断试验评价体系：构建ROC分析的基石

ROC分析的起点是构建一个基于真实类别与预测结果的混淆矩阵。理解这个矩阵及其衍生指标，是解读ROC曲线的关键。

（一） 混淆矩阵：所有故事的开始

对于一个二分类问题（如患病/健康、阳性/阴性），将预测结果与金标准（真实情况）对比，可得到一个2x2的配对四格表，即混淆矩阵。

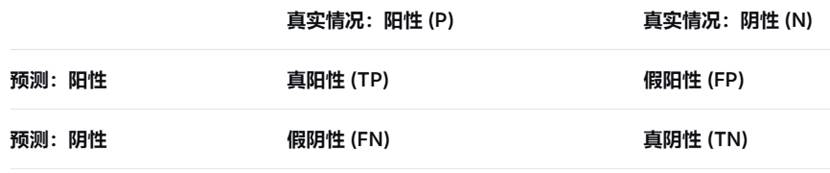
这个矩阵中的四个核心计数（TP, FP, FN, TN）是所有评价指标的源头。

（二） 核心评价指标：从不同角度审视性能

基于混淆矩阵，可以计算出一系列反映分类器不同方面能力的指标。下图展示了从原始数据到核心评价指标的计算逻辑与解读方向。

指标详解：

• 敏感度：又称真阳性率，反映了模型“不错过”阳性样本的能力。在医疗中，高敏感度的测试适用于筛查严重疾病（如癌症），宁可误报也不可漏报。
• 特异度：又称真阴性率，反映了模型“不冤枉”阴性样本的能力。在确诊或特异性高的场景下（如HIV确诊），需要极高的特异度。
• 精确度：又称阳性预测值，反映了当模型预测为阳性时，这个预测有多可信。在垃圾邮件过滤中，我们更关心被标记为垃圾的邮件中，有多少真是垃圾。
• 准确率：最简单的全局指标，但在类别不平衡时极易产生误导。
• 约登指数：一个综合评价指标，其最大值对应的阈值，通常被认为是敏感度与特异度的最佳平衡点。

二、 ROC曲线的核心原理：超越单一阈值

（一） ROC曲线的绘制逻辑

上述所有指标（除准确率外）都依赖于一个预设的分类阈值。例如，在医学检测中，血清某项指标高于某个临界值判为阳性。但阈值的选择是主观的：提高阈值，特异度增加但敏感度下降；降低阈值，则相反。

ROC曲线的天才之处在于，它不固定于单一阈值，而是动态地描绘出分类器在所有可能阈值下的性能表现。

绘制步骤：

1. 对于一个能够输出连续概率值或分数的分类器（如逻辑回归的预测概率、SVM的决策函数值），将其所有预测值从大到小排序，依次作为候选阈值。
2. 以每一个候选阈值为准，计算对应的 真阳性率 和 假阳性率。
3. 在二维坐标系中，以 FPR (1 - 特异度) 为横坐标，TPR (敏感度) 为纵坐标，将所有点连接起来，即得到ROC曲线。

（二） ROC曲线的解读：图形中的智慧

一条典型的ROC曲线及其解读区域如下图所示，不同的曲线形态揭示了分类器内在的性能差异。

• 完美分类器：曲线从左下角(0,0)垂直上升至左上角(0,1)，然后水平到达右上角(1,1)。这意味着存在一个阈值可以实现100%的敏感度和100%的特异度。
• 优秀/良好分类器：曲线明显向左上角凸起，越接近左上角越好。
• 随机猜测线：从(0,0)到(1,1)的对角线。这条线代表一个没有任何判别能力的分类器（如抛硬币），其AUC=0.5。任何有意义的分类器其曲线都应位于该对角线的左上方。
• 曲线下区域：曲线与对角线之间的面积越大，分类器的整体判别能力越强。

三、 AUC值：量化分类器的整体性能

（一） AUC的定义与计算

曲线下面积是ROC曲线最核心的量化指标。其值在0.5到1.0之间。

• AUC = 1.0：完美分类器。
• AUC = 0.5：等同于随机猜测。
• 0.5 < AUC < 1.0：具有一定判别能力。通常认为：
• 0.7 ≤ AUC < 0.9：具有较高的判别价值（常见于实用的诊断试验或模型）。
• AUC ≥ 0.9：具有非常高的判别价值（优秀）。
• AUC < 0.5：比随机猜测还差，通常意味着分类器的定义可能被颠倒了（将阳性预测为阴性的概率更高）。

AUC的统计意义是：随机选取一个阳性样本和一个阴性样本，分类器将阳性样本的得分判为高于阴性样本得分的概率。这使得AUC成为一个对类别不平衡不敏感的优秀指标。

（二） AUC的统计推断与比较

在实际研究中，我们不仅需要点估计的AUC值，还需要其置信区间，以评估估计的精确度。更重要的是，经常需要比较两个或多个诊断方法或模型的AUC是否存在统计学差异。

常用比较方法：

• Hanley & McNeil法（适用于独立样本）：当两种诊断方法应用于不同组的受试者时使用。需要输入两个AUC值及其标准误，通过构造Z统计量进行检验。
• DeLong检验（适用于配对样本）：当两种诊断方法应用于同一组受试者时（最常见的情况，如比较新旧两种检测方法），DeLong检验是更优选择。它考虑了AUC估计值之间的相关性，检验效能更高。在现代统计软件中，这已成为标准配置。

假设：H0: AUC1 = AUC2；H1: AUC1 ≠ AUC2。

若p值小于显著性水平（如0.05），则拒绝原假设，认为两个分类器的AUC存在显著差异。

四、 进阶应用：联合诊断与模型优化

（一） 联合诊断：1+1>2的策略

在临床实践中，单一指标往往不足以做出准确判断。联合诊断旨在结合多个指标的信息，以期获得比任何单一指标都更优的诊断性能。

实现方法（以两指标为例）：

1. 逻辑回归融合法（最常用且灵活）：将多个诊断指标作为自变量，金标准结果作为因变量，建立一个二元逻辑回归模型。该模型输出的预测概率值，综合了所有指标的信息。将此预测概率作为新的“联合诊断指标”进行ROC分析，所得的AUC即代表了联合诊断的效能。
2. 其他方法：还包括如线性判别分析、以及更简单的“并联试验”（任一阳性即判为阳性，提高敏感度）和“串联试验”（所有阳性才判为阳性，提高特异度）等策略。

逻辑回归法的优势在于，它通过数据驱动的方式自动学习各指标的最佳权重，并能处理指标间的交互作用，通常能产生最优的联合诊断效果。

（二） ROC分析在机器学习中的延伸应用

在机器学习领域，ROC分析被广泛用于模型选择、阈值确定和性能监控。

• 模型选择：在交叉验证中，比较各候选模型在验证集上的平均AUC，选择AUC最高的模型。
• 阈值确定：根据业务需求确定阈值。若追求高敏感度（如疾病筛查），可选择曲线上敏感度较高的点对应的阈值；若追求高特异度（如垃圾邮件过滤），则选择假阳性率较低的点。
• 多分类问题：ROC分析可推广至多分类，常用方法有“一对多”，即为每个类别分别绘制一条ROC曲线（将该类作为阳性，其余所有类作为阴性）。

五、 实践案例与软件实现

假设我们评估两种肿瘤标志物（test1，test2）对某种癌症的诊断价值。金标准为病理活检。

分析步骤：

1. 数据准备：整理数据，包含三列：diag（金标准，0=阴性，1=阳性）、test1，test2（均为连续数值）。
2. 绘制ROC曲线：将diag作为状态变量，test1，test2作为检验变量，可一次生成两条ROC曲线进行直观对比。
3. 解读结果：

查看AUC值及其95%置信区间。例如，test1的AUC=0.947(0.900-0.994)，test2的AUC=0.679 (0.574-0.784)。

观察曲线，test1的曲线更靠近左上角。

1. 比较AUC：由于是对同一批患者的两种检测，使用DeLong检验。结果显示p=0.00 < 0.05，说明test1的诊断效能显著优于test2。

1. 确定最佳阈值：根据约登指数最大值，确定最佳界值、敏感度、特异度、cut-off等值。

1. 尝试联合诊断：SPSSAU分析前勾选【联合诊断】按钮即可。

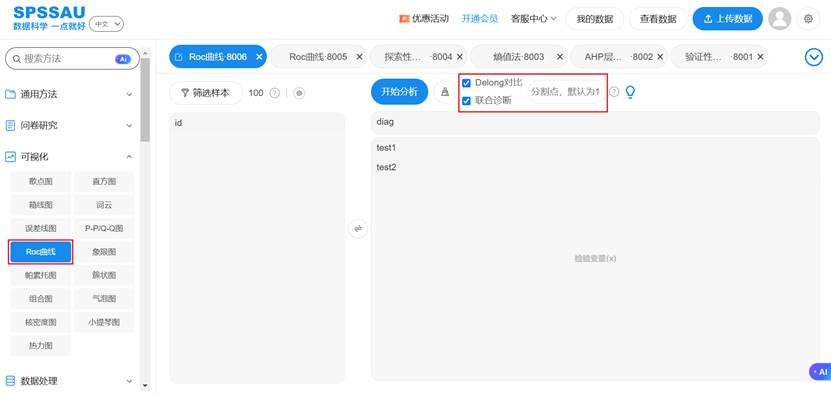
软件实现：以SPSSAU平台为例，其【可视化】模块下的【ROC曲线】分析功能，能够一站式完成上述所有步骤：自动绘制多条曲线、计算AUC及置信区间、进行DeLong检验、并直接输出最佳截断值及其对应的敏感度与特异度。对于联合诊断，其内置的【二元Logit回归】与ROC分析模块可实现无缝衔接，用户只需勾选“保存预测值”，即可将该预测值作为新变量直接用于后续的ROC分析，极大地简化了工作流程。SPSSAU操作示例如下：

结论

ROC分析不仅是一种统计工具，更是一种决策科学思维的体现。它迫使研究者正视分类问题中固有的权衡：敏感度与特异度、召回率与精确度、查全与查准。通过将这种权衡关系可视化、量化，ROC曲线为我们提供了在不同应用场景下做出最优决策的科学依据。