二元Logit回归全流程深度解析：从模型构建到结果解读

一、二元Logit回归与SPSSAU

二元Logit回归是研究二分类因变量与多个自变量之间关系的经典统计方法，广泛应用于医学、金融、社会科学等领域。当因变量只有两种可能结果（如是否违约、是否患病、是否购买）时，Logit回归能够有效分析各因素对结果发生概率的影响程度。

作为一款智能数据分析平台，SPSSAU为用户提供了完整的二元Logit回归分析解决方案，从数据预处理、模型构建到结果解读，全流程自动化处理，大大降低了复杂统计方法的使用门槛。本文将系统解析二元Logit回归的完整分析框架，展示SPSSAU如何简化和优化这一分析过程。

二、二元Logit回归分析全流程

SPSSAU中的二元Logit回归分析遵循严谨的统计流程，确保分析结果的科学性和可靠性。以下是完整的分析步骤：

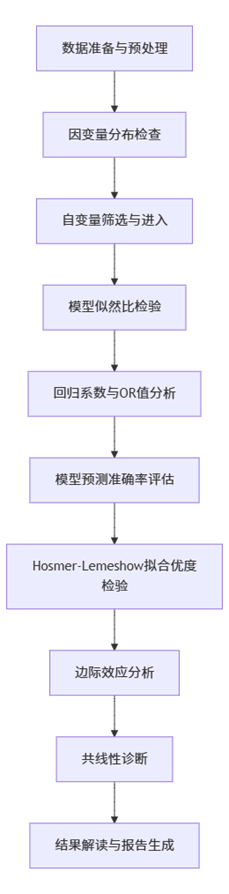
该流程图清晰地展示了二元Logit回归在SPSSAU中的完整分析路径。从数据准备开始，系统首先检查因变量的分布情况，确保符合方法要求；接着通过自动筛选机制将符合条件的自变量纳入模型；然后进行多轮统计检验，包括模型整体有效性检验、系数显著性检验、预测准确率评估和拟合优度检验；最后提供边际效应分析和共线性诊断，确保模型稳定可靠。这一系统化流程保证了分析结果的科学性和实用性。

三、关键指标解析与分类

3.1 模型基本设置与数据概况

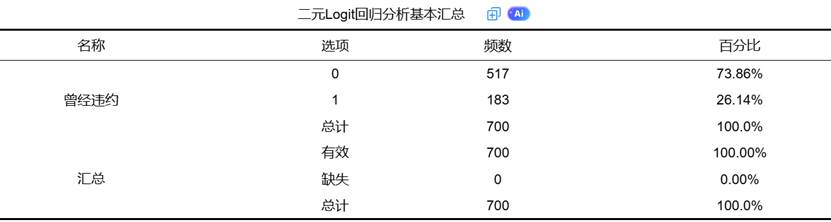
在二元Logit回归中，首先需要确认数据的基本情况，这是模型构建的基础。SPSSAU会自动提供数据概览，包括因变量分布、有效样本量等信息。

因变量分布：二元Logit回归要求因变量必须是二分类变量，且编码为0和1。分析前需要检查两类别的分布比例，避免因某一类别占比过低而影响模型稳定性。

样本量 adequacy：足够的样本量是模型估计准确性的保障。一般来说，每个自变量至少需要10-15个事件数（较少类别的观测值），SPSSAU会提示样本量是否满足分析要求。

3.2 模型整体有效性检验

模型似然比检验是评估模型整体有效性的核心指标，它比较了包含自变量的模型与仅含截距项的模型之间的差异。

似然比检验通过卡方统计量检验纳入的自变量是否显著改善了模型拟合效果。当p值小于显著性水平（通常为0.05）时，表明纳入的自变量整体上对因变量有显著解释力，模型构建有意义。AIC和BIC值则用于模型比较，数值越低表明模型越简洁高效，这在模型选择时尤为重要。

3.3 回归系数与OR值分析

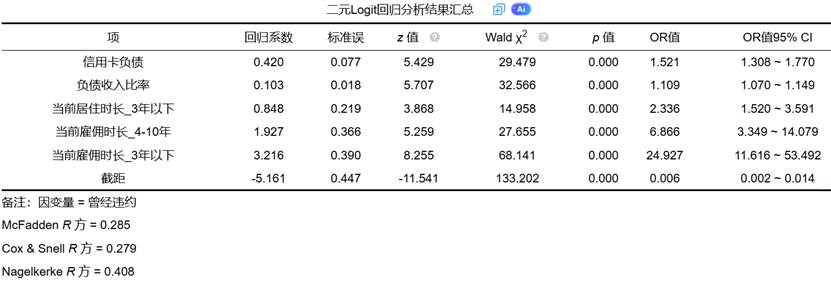
回归系数和OR值是Logit回归的核心结果，反映了自变量对因变量的影响方向和强度。

• 回归系数：表示自变量每变化一个单位，因变量对数发生比的变化量。正系数表示自变量增加会提高事件发生概率，负系数则相反。
• OR值：优势比，是回归系数的指数函数，表示自变量每变化一个单位，事件发生比的倍数变化。OR值大于1表示正影响，小于1表示负影响，等于1表示无影响。
• Wald统计量：用于检验单个回归系数的显著性，服从卡方分布。当对应的p值小于0.05时，表明该自变量对因变量有显著影响。
• 置信区间：为OR值提供区间估计，反映估计的精确度。区间不包含1时，表明影响统计显著。

3.4 模型预测与拟合优度

模型预测准确率和Hosmer-Lemeshow检验是评估模型拟合效果的重要指标。

（1）预测准确率：通过交叉表形式展示模型对因变量类别的预测能力，包括整体预测准确率和各类别的预测准确率。一个理想的模型应在两个类别上都有较高的预测准确率。

（2）Hosmer-Lemeshow检验：评估模型预测概率与实际观测结果之间的一致性。当p值大于0.05时，表明模型拟合良好，预测值与观测值无显著差异。

伪R方：包括McFadden、Cox & Snell和Nagelkerke R方，用于衡量模型对因变量变异的解释程度，类似于线性回归中的R方，但解释略有不同。

3.5 边际效应与模型诊断

（1）边际效应：表示自变量在平均值处每增加一个单位，因变量为1的概率变化量。它提供了比OR值更直观的解释，特别在政策分析和业务决策中更为实用。

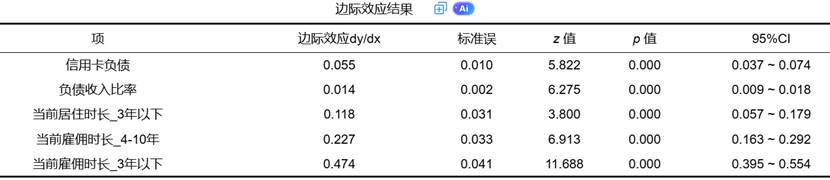
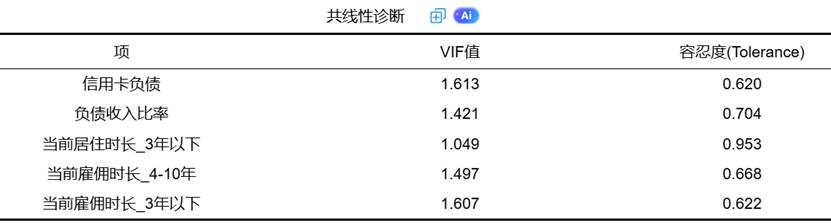
（2）共线性诊断：通过方差膨胀因子和容忍度判断自变量间的多重共线性问题。VIF值大于10或容忍度小于0.1表明存在严重共线性，可能影响系数估计的稳定性。

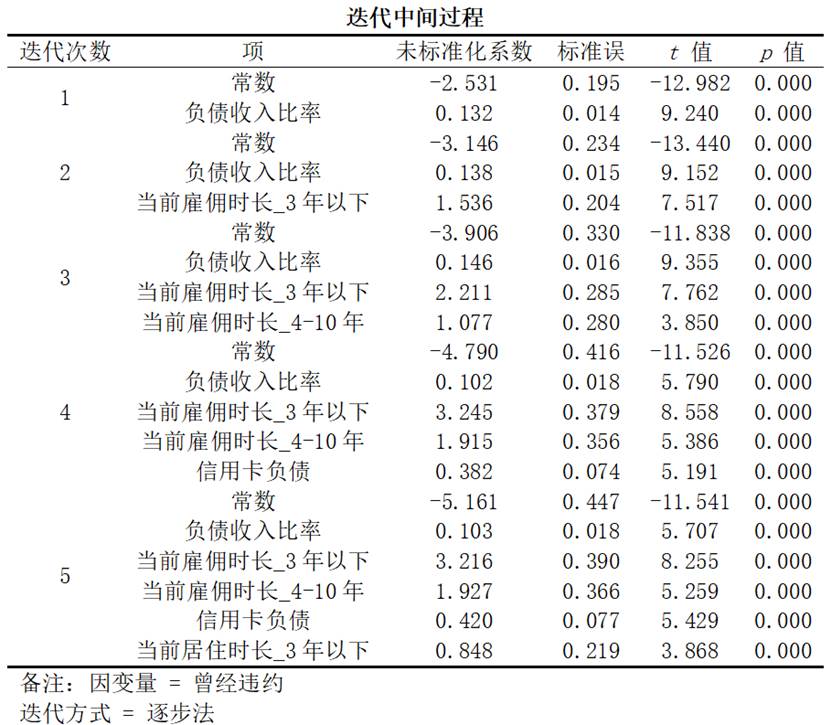
（3）迭代过程：展示模型构建过程中变量的进入和退出情况，反映了逐步法筛选自变量的逻辑和步骤。

四、指标间关联性与理论框架

二元Logit回归中的各项指标并非孤立存在，而是构成了一个完整的推断体系，相互印证、相互支持。

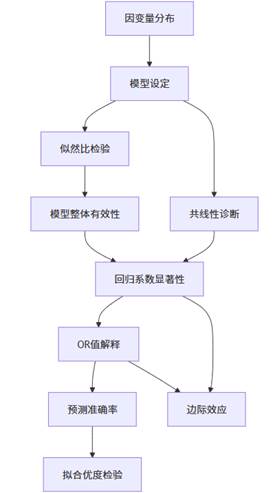
上图展示了二元Logit回归中关键指标之间的逻辑关系。首先，因变量分布决定了模型的基本设定；模型整体有效性通过似然比检验确认；在此基础上，单个自变量的影响通过回归系数和OR值评估；而预测准确率和拟合优度检验则从不同角度验证模型的实用价值；边际效应将模型结果转化为更直观的概率变化；共线性诊断确保系数估计的稳定性。这一完整的证据链确保了模型结果的科学性和可靠性。

特别需要注意的是，模型整体有效性与单个自变量显著性的关系：即使模型整体有效，也可能包含不显著的自变量；反之，模型整体无效时，单个自变量的显著性也缺乏意义。因此，在解读结果时，应从整体到局部，循序渐进。

五、逐步法、向前法、向后法

SPSSAU进行二元Logistic回归分析时，自变量进入模型的方式有‌全进入法（默认）、逐步法（基于Wald p）、向前法（基于Wald p）、向后法（基于Wald p）‌，操作如下图：

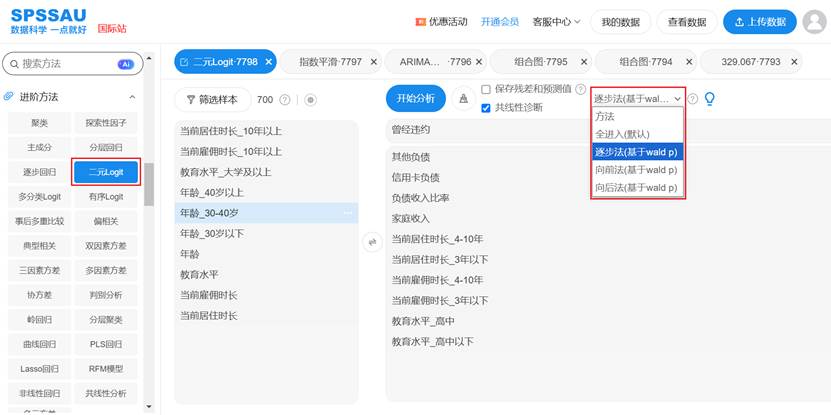
1. 全进入法（默认）

所有候选自变量‌一次性全部进入‌回归模型，无需筛选过程。适用于自变量数量少、研究者对所有自变量的预测作用均需保留的场景（如理论明确所有变量均需纳入分析）。

2. 逐步法（基于Wald p）

通过‌“进-出”双向筛选‌实现自变量选择：

• 初始模型无自变量，逐步加入显著性（Wald p值）达标的自变量；
• 若已进入模型的自变量后续因Wald p值不显著被剔除，或新变量加入后使原显著变量不显著，也会被剔除；
• 迭代过程持续至无变量满足“进入/剔除”条件，最终模型包含对因变量预测最稳定的自变量组合。

3. 向前法（基于Wald p）

以‌“逐步加入”‌为核心逻辑：

• 初始模型无自变量，每次仅加入一个Wald p值最显著的自变量；
• 每次加入后重新评估模型，若新变量加入后使原显著变量不显著，原变量会被剔除；
• 迭代至无变量满足“加入”条件，最终模型为逐步筛选出的最优自变量组合。

4. 向后法（基于Wald p）

以‌“逐步剔除”‌为核心逻辑：

• 初始模型包含所有候选自变量，每次剔除一个Wald p值最不显著的自变量；
• 每次剔除后重新评估模型，若剔除后使原不显著变量显著，原变量会被重新加入；
• 迭代至无变量满足“剔除”条件，最终模型为逐步筛选出的最优自变量组合。

这三类方法通过不同筛选逻辑，帮助研究者在自变量众多时高效选择对因变量预测价值最高的变量，平衡模型复杂度与预测能力。

六、结论与SPSSAU价值体现

二元Logit回归作为一个复杂的统计方法，涉及众多概念和指标，传统统计软件往往需要用户具备相当的统计知识才能正确理解和解读。SPSSAU通过自动化、智能化的分析流程，将这一复杂过程简化为几个点击操作，同时保持了方法的严谨性和结果的完整性。

SPSSAU为二元Logit回归提供了丰富的结果表格，每张表格都有其特定的理论和实用价值。SPSSAU的智能分析功能自动解读每张表格的理论意义和实用价值，大大节省了用户的学习成本和解读时间。