典型相关分析的操作步骤与结果解读方法

一、典型相关分析：揭示两组变量之间的深层关联

典型相关分析（Canonical Correlation Analysis, CCA）是多元统计分析中的重要方法，专门用于研究两组变量之间的相关关系。与简单相关分析只能研究两个变量之间的关系不同，CCA能够同时探究两组变量集合之间的内在联系，在心理学、教育学、医学和体育科学等领域有着广泛应用。

举个例子，在体育科学研究中，我们可能关心身体素质指标（如反复横向跳、纵跳、背力等）与运动表现指标（如50米跑、跳远、投球等）之间的关系。CCA正是解决这类问题的理想工具，它能够找出两组变量背后的共同结构，揭示它们之间的本质联系。

随着统计软件的发展，进行典型相关分析已变得十分便捷。SPSSAU作为一款在线数据分析工具，提供了用户友好的CCA分析模块，使研究者无需编程即可完成复杂的多元统计分析。本文将基于SPSSAU的实际输出，详细介绍典型相关分析的操作步骤与结果解读方法。

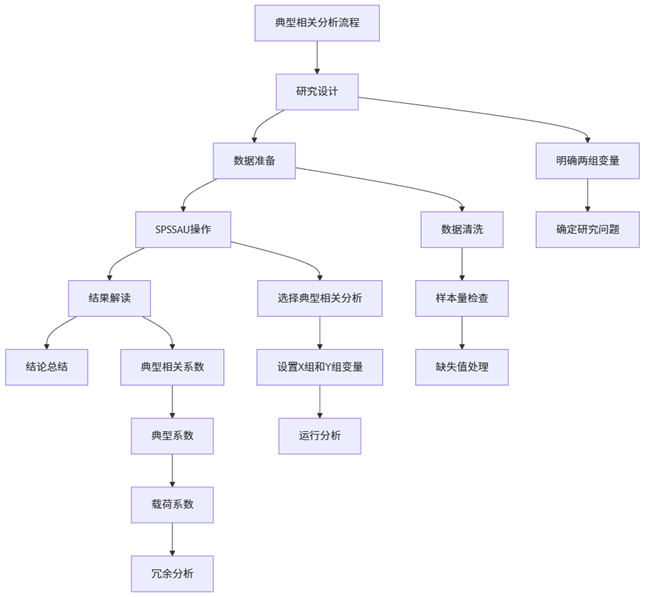
如上图所示，典型相关分析遵循一套系统的流程，从研究设计开始，经过数据准备、软件操作，最终到结果解读。每个环节都有其特定的要求和注意事项，我们将在下文详细展开。

二、典型相关分析的操作步骤

2.1 研究设计与数据准备

进行典型相关分析前，首先需要明确研究问题并确定两组变量。在本案例中，X组变量包括7项身体素质指标：反复横向跳、纵跳、背力、握力、台阶试验、立定体前屈和俯卧上体后仰；Y组变量包括5项运动表现指标：50米跑、跳远、投球、引体向上和耐力跑。

数据准备阶段需注意以下几点：

• 样本量应充足，一般建议样本数至少是变量数的10-20倍
• 检查变量间的线性关系，CCA基于线性假设
• 处理缺失值，确保数据完整
• 考虑变量标准化，避免量纲影响

从提供的SPSSAU输出中可以看到，本案例共有38个有效样本，无缺失数据，满足分析的基本要求。

2.2 SPSSAU操作流程

SPSSAU平台简化了典型相关分析的操作过程，具体步骤如下：

1. 选择分析方法：在"多元统计"模块中选择"典型相关分析"
2. 设置变量组：将X组变量（身体素质指标）和Y组变量（运动表现指标）分别放入对应框
3. 运行分析：点击"开始分析"即可得到完整结果，操作示例如下：

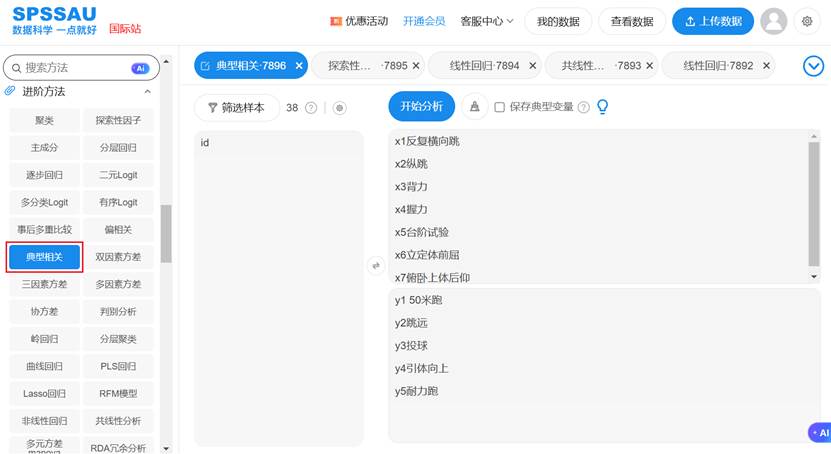
SPSSAU会自动完成模型拟合和结果计算，输出包括典型相关系数、典型系数、载荷系数和冗余分析等全面信息，大大提高了分析效率。

三、典型相关分析结果解读

3.1 典型相关系数及显著性检验

典型相关分析首先会提取一系列典型变量对，每对包括一个来自X组的典型变量和一个来自Y组的典型变量。首当其冲的是评估这些典型变量对之间的相关关系是否显著。

从SPSSAU输出表格中，我们可以看到：

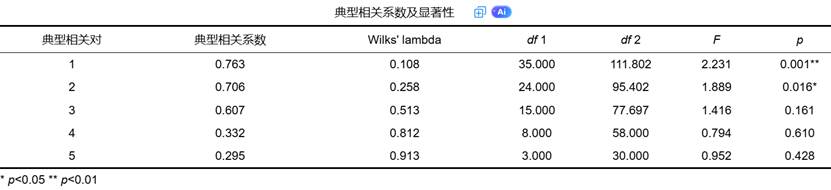
• 典型相关系数：表示典型变量对之间的相关程度，范围从0到1，值越大表示关系越强。第一对典型变量的相关系数为0.763，表明它们之间有较强的相关性。
• 显著性检验：基于Wilks' lambda统计量，p值小于0.05表示典型相关关系显著。本分析中，前两对典型变量在统计上显著（p<0.05），说明X组和Y组变量间确实存在显著的相关结构。
• 实际意义：身体素质指标与运动表现指标之间存在显著关联，且这种关联主要通过两个独立的维度体现。

3.2 典型系数与典型变量构建

典型系数用于构建典型变量，表示各原始变量在典型变量中的权重。SPSSAU分别提供了X组和Y组的典型系数表格。

X组典型系数表格显示：

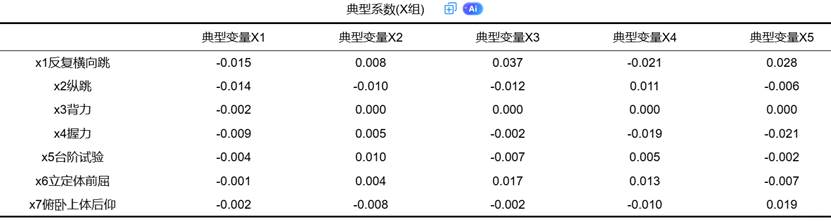
根据典型系数，我们可以构建典型变量的数学表达式。例如：
典型变量X1 = -0.015×x1反复横向跳 - 0.014×x2纵跳 - 0.002×x3背力 - 0.009×x4握力 - 0.004×x5台阶试验 - 0.001×x6立定体前屈 - 0.002×x7俯卧上体后仰

需要注意的是，典型系数仅从数学角度表达变量间关系，其数值大小并不直接代表变量的实际重要性。由于典型系数受变量量纲和共线性影响，解释时需谨慎。

3.3 典型载荷系数：解读变量贡献

典型载荷系数（也称结构系数）表示原始变量与典型变量之间的相关关系，更能反映变量的实际贡献。SPSSAU输出的载荷系数表格提供了更为直观的结果。

X组典型载荷系数表格显示：

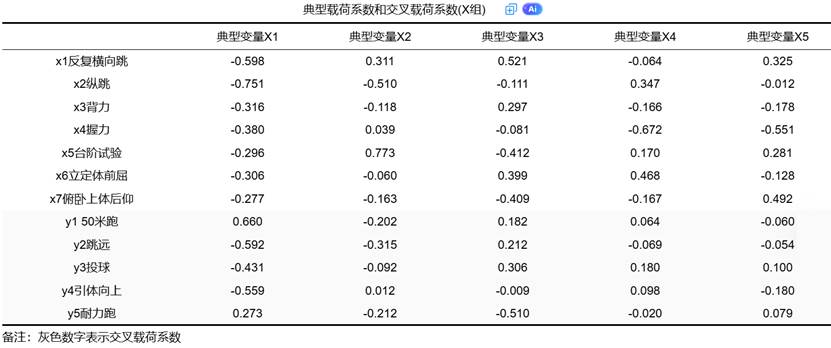
• 载荷系数绝对值：通常使用绝对值进行评估，值越大表示该变量与典型变量的关系越紧密。一般以0.3或0.4为临界点，判断变量是否对典型变量有重要贡献。
• 第一典型变量X1：纵跳(-0.751)和反复横向跳(-0.598)载荷较高，表明第一典型变量主要代表爆发力素质。
• 第二典型变量X2：台阶试验(0.773)载荷最高，表明第二典型变量主要代表心肺耐力素质。

通过分析载荷系数，我们可以为每个典型变量赋予实际意义，便于理解和解释结果。SPSSAU提供的载荷系数表格清晰展示了各变量对不同典型变量的贡献度，大大简化了解读过程。

交叉载荷系数表示典型变量与另一组变量之间的关系，如典型变量X与Y组变量之间的相关关系。这一指标有助于理解两组变量之间的交叉影响。

从SPSSAU输出中，我们可以看到典型变量X1与Y组变量的交叉载荷系数。

• 关系方向：正值表示正相关，负值表示负相关。例如，典型变量X1与50米跑正相关(0.660)，与跳远负相关(-0.592)。
• 实际意义：典型变量X1（代表爆发力）与50米跑正相关，表明爆发力强的学生50米跑成绩更好（时间短，数值大）；与跳远负相关则需谨慎解释，可能由于数据特性或变量编码方式导致。
• 结果应用：交叉载荷系数揭示了身体素质与运动表现之间的具体关联模式，为体育训练计划制定提供了理论依据。

3.5 典型冗余分析：解释力度评估

冗余分析用于评估典型变量对原始变量信息的解释能力，包括组内解释和组间解释。SPSSAU提供的冗余分析表格如下：

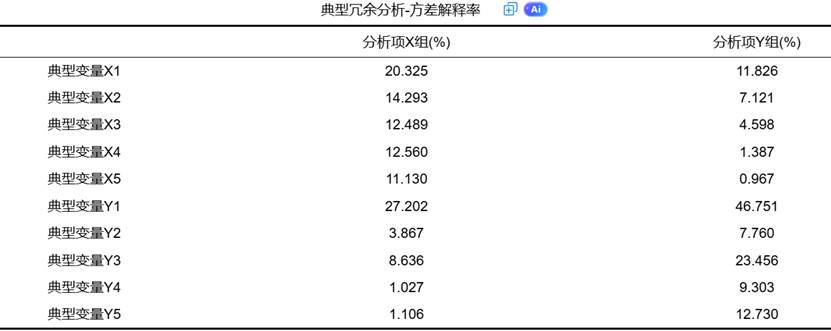
• 组内解释：典型变量对同组变量变异解释的比例。例如，前两个典型变量X累计可解释X组变量34.618%的信息（20.325%+14.293%）。
• 组间解释：典型变量对另一组变量变异解释的比例。例如，典型变量X1可以解释Y组变量11.826%的信息。
• 实际意义：前两个显著典型变量累计可解释X组变量34.62%的信息，解释Y组变量54.51%的信息，说明身体素质指标可以较好地预测运动表现。

冗余分析结果帮助我们评估典型相关模型的实用价值，解释率越高，模型的应用意义越大。

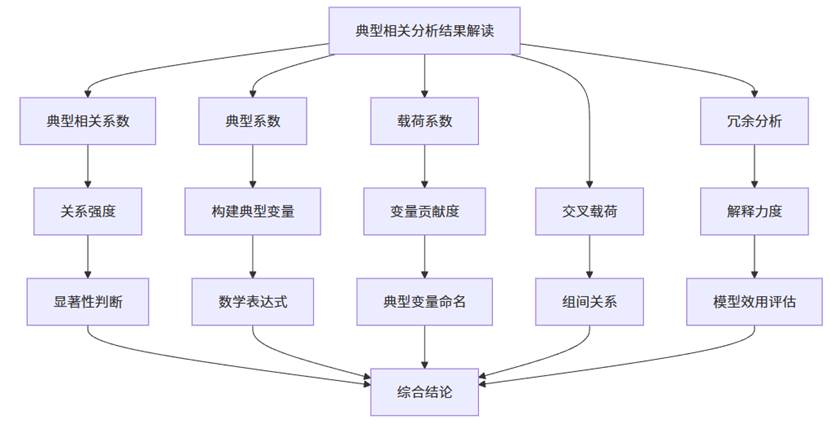
典型相关分析的结果解读是一个系统工程，需要从多个角度综合考虑。SPSSAU输出的完整结果表格为这种综合解读提供了便利，研究者可以按部就班地评估模型各方面特征，最终形成科学结论。

四、典型相关分析的应用建议与总结

4.1 分析结果总结

基于SPSSAU输出的全面分析，我们可以得出以下结论：

1. 身体素质与运动表现关系密切：典型相关分析结果显示，两组变量之间存在显著的典型相关关系，前两对典型变量均通过显著性检验。
2. 两维度主导关系：身体素质与运动表现的关系主要通过两个独立维度体现：第一个维度代表爆发力（由纵跳和反复横向跳主导），与50米跑密切相关；第二个维度代表心肺耐力（由台阶试验主导），与耐力跑相关。
3. 模型解释力度良好：前两对典型变量累计可解释X组变量34.62%的信息，解释Y组变量54.51%的信息，表明模型具有较好的解释能力。

4.2 典型相关分析的注意事项

在进行典型相关分析时，需要注意以下几点：

1. 样本量要求：典型相关分析需要足够的样本量，一般建议样本数至少是变量数的10-20倍。本案例中样本量为38，变量总数为12，比例约为3:1，略低于理想标准，这在解释结果时需保持谨慎。
2. 变量选择：理论上应包括所有相关变量，但高度相关的变量可能导致共线性问题。必要时可先进行变量筛选或主成分分析。
3. 结果验证：建议将数据随机分成两部分，一部分用于探索性分析，另一部分用于验证性分析，确保结果的稳定性。
4. 结合专业知识：统计显著性不等于实际意义，结果解释必须结合领域专业知识。例如，本研究中典型变量X1与跳远的负相关关系需要从体育科学角度进一步探讨。

4.3 SPSSAU在典型相关分析中的优势

通过本案例的分析过程，我们可以看出SPSSAU在典型相关分析中的多项优势：

1. 操作简便：直观的界面设计使得复杂的多元统计分析变得简单易行，无需编写代码。
2. 输出全面：提供典型相关系数、典型系数、载荷系数和冗余分析等完整结果，满足专业分析需求。
3. 解释清晰：智能分析功能自动生成结果解释，帮助用户理解统计输出。
4. 节省时间：自动化计算过程大大减少了分析时间，使研究者能专注于结果解释和应用。

典型相关分析作为一种强大的多元统计方法，能够揭示变量组间的复杂关系结构。结合SPSSAU这样的专业工具，研究者可以更加高效地开展数据分析工作，从数据中提取有价值的科学洞见。