一元线性回归与多重线性回归的区别

1. 基本概念差异

一元线性回归（简单线性回归）： 仅包含一个自变量和一个因变量，回归方程形式：y = a + bx - 例如：分析食物含糖量对糖尿病患病率的影响

多重线性回归（多元线性回归）：包含多个自变量和一个因变量，回归方程形式：y = b₀ + b₁x₁ + b₂x₂ + ... + bₙxₙ，例如：研究产品质量、服务、营业时间等多因素对客户满意度的影响

2. 核心区别对比

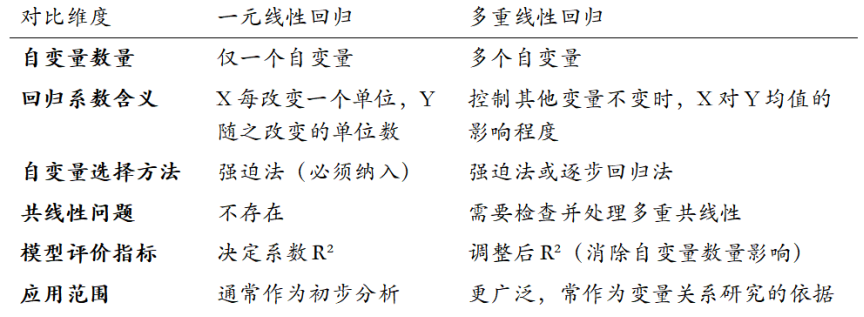
3. 技术细节差异

1. 模型假设不同：
   • 多重线性回归比一元线性回归多一个"解释变量间不存在严格线性相关"的假设
   • 多重线性回归需要进行多重共线性诊断（通过VIF值等）
2. 计算复杂度：
   • 一元线性回归只需建立二元方程组
   • 多重线性回归需建立m元正规方程组，通常需要矩阵运算
3. 检验方式：
   • 一元线性回归中，方程检验与系数检验效果等价
   • 多重线性回归中，方程检验包含多个自变量关系的综合检验

4. SPSSAU(在线SPSS)应用建议

1. 操作步骤：
   • 在SPSSAU(网页SPSS)中，两种回归分析路径相同：【通用方法】→【线性回归】
   • 区别仅在于自变量的选择数量
2. 结果解读：
   • 一元线性回归重点关注单个回归系数的显著性
   • 多重线性回归需同时关注：
     • 整体模型显著性(F检验)
     • 各自变量的显著性(t检验)
     • 共线性统计量(VIF值)
3. 模型选择：
   • 当研究单一因素影响时，使用一元线性回归
   • 当考虑多因素综合影响时，使用多重线性回归
   • 在SPSSAU中可通过"逐步回归"功能自动筛选重要变量

5. 实际应用建议

1. 初步分析：可先进行一元线性回归，了解各变量单独的影响
2. 深入分析：再通过多重线性回归建立综合模型
3. 注意事项：
   • 多重线性回归需确保样本量足够(一般每个自变量需要10-15个样本)
   • 分类变量需要先进行虚拟变量处理
   • 异常值可能对结果产生较大影响

如需在SPSSAU(在线SPSS)中进行这两种分析，可参考平台提供的帮助手册，确保分析过程的规范性和结果的可靠性。