随机前沿分析SFA理论、软件操作与分析结果解读

最新推荐文章于 2025-12-15 22:32:00 发布

原创最新推荐文章于 2025-12-15 22:32:00 发布 · 851 阅读

CC 4.0 BY-SA版权

文章标签：

随机前沿分析(Stochastic Frontier Analysis, SFA)是一种用于测量技术效率的计量经济学方法。其可以用来评估决策单元(如企业、农场等)相对于最佳实践前沿面的技术效率。类似DEA数据包络分析研究投入和产出效率关系，SFA使用统计方式来计算（DEA是使用求解器方式）。其数学原理如下：

SFA模型将传统的生产函数或成本函数中的误差项分解为两个部分：

随机误差项（v）：代表统计噪声，可正可负
技术无效率项（u）：代表技术无效率，通常为非负值

生产函数时：y = f(x, β) + v – u

成本函数时：y = f(x, β) + v + u

其中：y：产出（生产函数）或成本（成本函数）；x：投入变量；β：待估参数；v：随机误差项，通常假设服从正态分布；u：技术无效率项，通常假设服从半正态分布或其他非负分布。

SFA模型广泛应用于以下领域：企业效率评估：评估制造业、服务业等企业的生产效率，银行业分析：分析银行的成本效率和利润效率，农业研究：评估农场的生产效率，教育评估：分析学校或教育机构的效率，医疗绩效：评估医院或其他医疗机构的效率，公共部门：评估政府部门或公共服务的效率。

随机前沿分析案例

1 背景

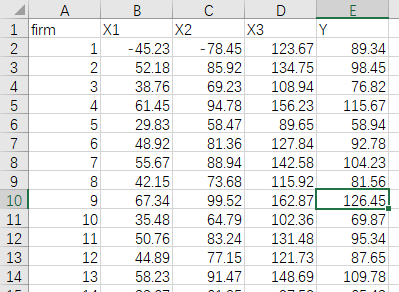
某研究机构收集了100家企业的投入产出数据，希望通过SFA分析评估这些企业的技术效率。数据包括3个投入变量(X1, X2, X3)和1个产出变量(Y)。研究目的是识别技术效率较低的企业，并分析影响效率的因素，部分数据如下。

2 理论

SFA包括生产函数和成本函数两种形式，通过构造数学模型公式，并且利用极大似然法进行数学求解，与此同时，SFA共包括三种技术效率估计方法，分别是Jondrow等(1982)提出的条件均值方法、Battese和Coelli(1988)提出的MSE最小化法（均方误差最小化法），Jondrow等(1982)提出的条件众数方法。相对来讲MSE最小化法可能使用相对更多。

分析上，首先应该确认是生产函数还是成本函数，并且选择技术效率估计方法（也或者三种估计方法进行对比），另外，SPSSAU中还提供数据取对数功能，包括对X或Y进行取对数处理。以及SFA分析时最重要指标为技术效率TE值，该值介于0和1之间。TE=1表示生产单位位于前沿面上，是完全技术有效率的；TE<1则表示存在无效率损失，越接近于1表示技术效率越高。TE值的获取上，可通过SPSSAU“保存信息”勾选后得到，分析完成后以新标题形式存储该数据。

3 操作

本案例操作截图和说明分别如下：

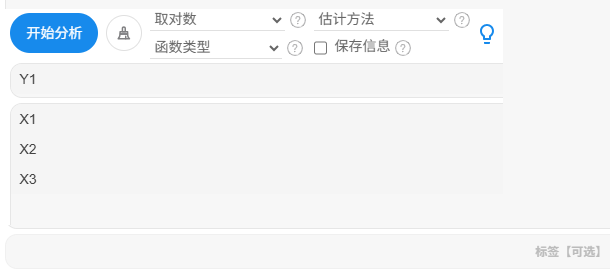
将X和Y分别放入右侧框中，右下方放入样本点的标签列数据，如果不放入，SPSSAU默认会输出比如第1项，第2项等内容。

关于‘取对数’
研究人员可自行下拉设置，默认是针对X和Y均取对数。以及取对数处理时，如果某列数据出现小于0则无法取对数，SPSSAU会自动进行‘非负平移’处理，即以该列为单位，均加上最小负数值的绝对数并且加上0.01，保证数据全部均大于0前提时再进行取对数处理。
关于‘估计方法’
建议研究人员尝试和对比该3种技术效率估计方法，分别是条件均值法、均方误差最小化法和条件众数法。通常使用条件均值或者均方误差最小化较多，可对比尝试使用，比如切换不同方法时查看AIC/BIC（该2指标越小越好），也或者对比Lambda值，该值越小越好。
关于‘函数类型’
默认是生产函数形式，可选为成本函数形式；生产函数更多关注产出能力或技术效率，成本函数更关注成本控制或成本效率。
关于‘保存信息’
如果选中该参数，SPSSAU会生成两个标题来存储指标数据，分别是技术效率TE和残差。

4 SPSSAU输出结果

SPSSAU中进行随机前沿分析时，其共输出7个表格，分别说明如下：

项	名称	说明
1	SFA基本参数表	显示SFA基本参数设置情况等
2	SFA模型似然比检验	显示似然比检验结果和信息准则(AIC、BIC)
3	参数估计表	显示模型参数估计值、标准误、t值、p值和置信区间
4	方差参数表	显示λ、σ²、σᵤ²、σᵥ²等方差参数
5	技术效率TE值	显示每个样本的技术效率估计值
6	技术效率统计指标	显示技术效率的均值、中位数、最小值、最大值和标准差
7	样本缺失情况汇总	展示真实进入算法模型时有效样本和排除在外的无效样本情况等

5文字分析

针对SFA分析，多数情况下需要对数据取对数后分析，对数变换通常可用于处理非线性关系和异方差性问题，使得模型更加稳定和易于解释，如果原始数据有小于等于0的数字，取对数时SPSSAU会自动进行‘非负平移’处理，平移单位为0.01；如果研究给定投入时最大化产出，那么则应该使用‘生产函数’，如果给出产出时研究最小化投入，此时应该使用‘成本函数’；多数情况下应该使用条件均值法（也或者均方误差最小化法）进行估计，当然也可尝试对比另外两种估计方法。

模型似然比检验用于对整体模型有效性进行分析。首先对p值进行分析，如果该值小于0.05，则说明模型有效；反之则说明模型无效；AIC和BIC值用于多次分析时的对比；此两值越低越好；如果多次进行分析，可对比此两个值的变化情况，综合说明模型构建的优化过程；
从上表可知：此处模型检验的原定假设为：是否放入投入变量（X1, X2, X3）两种情况时模型质量均一样；分析显示拒绝原假设（Chi=606.130，p=0.000<0.05），即说明本次构建模型时，放入的投入变量具有有效性，本次模型构建有意义。

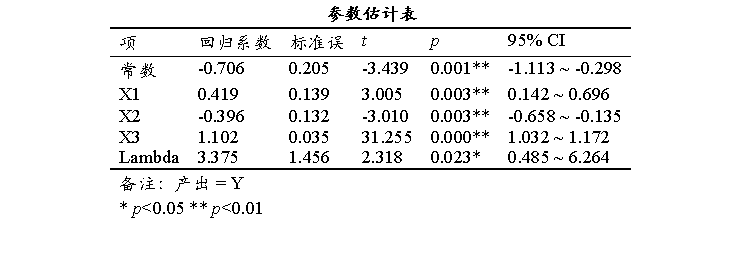
上表格展示投入变量对产出变量的影响关系，是否有影响关系，影响方向及影响程度情况如何；常数（截距）项表示模型的基准水平，其表示所有投入项为0时的预测值情况；接着分析投入项的显著性，如果呈现出显著性(p值小于0.05或0.01)，则说明投入项对产出有影响关系，接着具体分析影响关系方向，反之没有呈现出显著性，则意味着投入项并不会对产出产生影响；Lambda值反映了‘技术无效率项（u）’相对于‘随机误差项（v）’的相对重要性, λ=σᵤ / σᵥ，其中σᵤ 是技术无效率项的标准差,σᵥ是随机误差项的标准差；

Lambda值如果呈现出显著性则意味着‘技术无效率项’对模型有显著影响，反之说明‘技术无效率项’并没有对产出产生显著影响，Lambda值呈现出显著性时，此时该值越大时意味着‘技术无效率项’的影响越大。‘技术无效率项’ 指生产过程中由于管理不善/资源浪费/技术落后等因素导致的实际产出低于最大可能产出的程度，通常希望该指标值越小越好。

从上表可知，将X1, X2, X3共3项为投入变量，而将Y作为产出变量进行SFA模型构建，从上表可以看出，模型如下：Y = -0.70566 + 0.419*X1 - 0.396*X2 + 1.102*X3 + 3.375*Lambda + v - u最终具体分析可知：X1的回归系数值为0.419，并且呈现出0.01水平的显著性(p=0.003<0.01)，意味着X1会对Y产生显著的正向影响关系。X2的回归系数值为-0.396，并且呈现出0.01水平的显著性(p=0.003<0.01)，意味着X2会对Y产生显著的负向影响关系。X3的回归系数值为1.102，并且呈现出0.01水平的显著性(p=0.000<0.01)，意味着X3会对Y产生显著的正向影响关系。Lambda的回归系数值为3.375，并且呈现出0.05水平的显著性(p=0.023<0.05),意味着存在着显著的‘技术无效率’情况。

总结分析可知：X1, X2共2项会对Y产生显著的正向影响关系，以及X3会对Y产生显著的负向影响关系。以及Lambda呈现出显著性，其意味着生产过程中由于管理不善/资源浪费/技术落后等因素导致的实际产出低于最大可能产出的程度。

上表格是SFA模型的方差参数表格；公式上，σ² = σᵤ² + σᵥ²（误差项方差等于两个独立误差项方差之和），σᵤ² = λ² / (1 + λ²) × σ²（使用Lambda和总方差计算无效率方差），σᵥ² = σ² / (1 + λ²)（使用Lambda和总方差计算随机误差方差），λ = σᵤ/σᵥ（Lambda是两个标准差的比率）；σ²是总误差项的方差，表示模型中所有误差（包括技术无效率和随机误差）的总体波动程度。具体来说，它反映了观测值与模型预测值之间的总差异；σᵤ²表示由于技术无效率（如管理不善、资源浪费等）导致的产出低于最优水平的程度；σᵥ²表示由于不可控的随机因素（如市场波动、意外事件等）导致的观测值与模型预测值之间的差异；Lambda为技术无效率项标准差与随机误差项标准差的比值，其用于衡量技术无效率项与随机误差项的相对重要性。

提示：上表格中数字显示为0，可通过SPSSAU中设置小数位展示后查看，其并非刚好为0。

除此之外，SFA分析时非常关键的指标即技术效率TE值，其展示每个样本（每行数据，通常指每个企业公司等）的具体TE值，可通过针对TE值的具体分析来阐述竞争力情况，TE值介于0和1之间。TE=1表示生产单位位于前沿面上，是完全技术有效率；TE<1则表示存在无效率损失，越接近于1表示技术效率越高。与此同时TE值的获取上，可通过SPSSAU“保存信息”勾选后得到，分析完成后以新标题形式存储该数据，可用于进一步分析使用等。与此同时，SPSSAU还提供TE指标值的基础统计计算，包括平均值/中位数/最小或最大值/标准差信息等。