曲线回归分析的具体示例与软件操作步骤

曲线回归分析的具体示例与步骤

曲线回归分析是一种用于处理自变量与因变量之间非线性关系的统计方法。通过将非线性关系转换为线性关系，建立回归模型。以下是具体的示例和步骤，使用SPSSAU(在线SPSS)平台进行操作。

示例背景

假设我们有一组数据，研究儿童年龄与锡克氏实验阴性率之间的关系。数据包括两个变量：年龄（自变量）和阴性率（因变量）。我们的目标是拟合一个曲线回归模型，描述年龄与阴性率之间的关系。

具体步骤

1. 确认曲线关系
   • 绘制散点图：首先，我们需要绘制自变量（年龄）与因变量（阴性率）的散点图，观察二者之间的关系趋势。
     • 在SPSSAU(网页SPSS)平台中，进入【可视化】→【散点图】模块。
     • 将“年龄”设置为【X(定量)】横坐标，“阴性率”设置为【Y(定量)】纵坐标。
     • 绘制散点图后，观察点的分布趋势。如果趋势呈现非线性关系，则适合进行曲线回归分析。
2. 建立曲线模型
   • 选择曲线方程：根据散点图的走势，选择合适的曲线方程。常见的曲线方程包括二次曲线、三次曲线、对数曲线等。
     • 在SPSSAU(在线SPSS)平台中，进入【进阶方法】→【曲线回归】模块。
     • 将“年龄”放入【X(定量)】框，“阴性率”放入【Y(定量)】框。
     • 在顶部的下拉框中选择合适的曲线方程（如三次曲线、对数曲线等）。
     • 点击【开始分析】，SPSSAU将输出所选曲线方程的回归结果。
3. 模型检验和评价
   • 显著性检验：通过模型的方差分析结果，检验模型的总体显著性。如果p值小于0.05，说明模型具有统计学意义。
     • 查看SPSSAU输出的方差分析表，确认p值是否小于0.05。
   • 拟合质量评价：通过决定系数（R²）评价单个模型的拟合质量。R²越接近1，说明模型的拟合效果越好。
     • 查看SPSSAU输出的模型汇总表，比较不同曲线方程的R²值。
   • 模型比较：如果同时拟合了多个曲线方程，可以通过AIC、BIC等指标进行模型比较，选择最优模型。
     • 查看SPSSAU输出的AIC、BIC值，选择值较小的模型。
4. 综合报告
   • 报告最终模型：选择最优的曲线方程，报告其回归系数、显著性水平和拟合质量。
     • 在SPSSAU(网页SPSS)平台中，查看最优模型的回归系数表，记录各变量的偏回归系数及其p值。
     • 根据回归系数，写出最终的曲线方程。
     • 报告模型的R²值，说明模型对数据的解释能力。

示例结果

假设我们选择了三次曲线模型，SPSSAU输出的回归系数表如下：

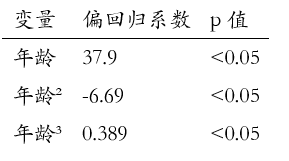
根据回归系数，三次曲线方程为：

该模型的R²值为0.995，说明模型可以解释阴性率99.5%的变异信息。

总结

通过以上步骤，我们可以在SPSSAU(在线SPSS)平台上完成曲线回归分析，选择合适的曲线方程，并对模型进行检验和评价。最终，我们可以得到一个有效的曲线回归模型，用于描述自变量与因变量之间的非线性关系。