【电路笔记 信号】信号能量在传输线中指数衰减+衰减系数特性+能量介质传播与指数衰减的关系+dB标度+功率指数衰减

1.从分布参数电路到电报方程

• 推导过程：微小线段电路模型 → 写出微分方程 → 解出指数解。整体和电路笔记(阻抗) : 传输线路方程&传输线输入阻抗公式 推导 + 理查德变换 Richards‘ Transformation（用传输线形式的分立元件替代集总元件）一样，只不过侧重的点不同。

1) 把电缆看成无限小段的分布参数模型

• 把长度 (x) 到 (x+dx) 的小段看作下面这个等效电路（串联 (R,dx), (L,dx)；并联 (G,dx), (C,dx)）。

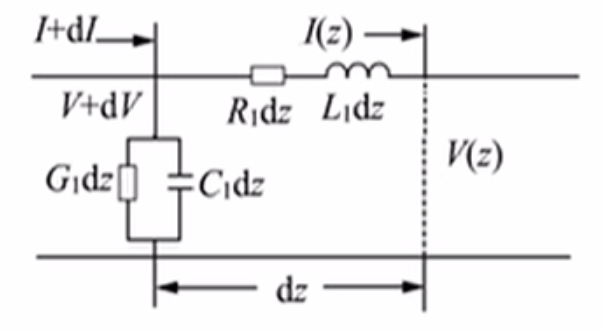
对于一条差分或单端传输线，每 单位长度 有四个参数（均为每米）：

• 电阻 R（Ω/m） — 串联耗散
• 电感 L（H/m） — 串联感抗
• 电导 G（S/m） — 对地漏导（介质损耗）
• 电容 C（F/m） — 对地或对相互线的电容

2) 写出微小段的基尔霍夫方程（KVL 与 KCL，在频域）

用复频域表示（假设信号为 $e^{j\omega t}$ 频率分量），对该小段：

• 电压降（KVL）：
  $$V(x)-V(x+dx)=(R,dx+j\omega L)\ast dx\ast I(x)$$
  两端差除以 (dx)，取极限：
  $$-\frac{\partial V}{\partial x}=(R+j\omega L)\ast I(x)\text{(1)}$$

• 电流连续方程（KCL）：流入与流出电流差等于并联支路的泄漏电流
  $$I(x)-I(x+dx)=(G,dx+j\omega C)\ast dx\ast V(x)$$
  类似化简得：
  $$-\frac{\partial I}{\partial x}=(G+j\omega C)\ast V(x)\text{(2)}$$

3) 消去 (I) 或 (V) 得到二阶微分方程（电报方程）

对式 (1) 两边对x求导，：

$$-\frac{{\partial }^{2}V}{\partial x^2}=(R+j\omega L)\ast \frac{\partial I}{\partial x}$$

将 (2) 代入：

$$\frac{{\partial }^{2}V}{\partial x^2}=(R+j\omega L)(G+j\omega C)\ast V$$

同理可以得到电流形式：

$$\frac{{\partial }^{2}I}{\partial x^2}=(R+j\omega L)(G+j\omega C)\ast I$$

4) 指数解

设
$${\gamma }^2=(R+j\omega L)(G+j\omega C)$$
则一阶解为
$$V(x)=V_{+}{e}^{-\gamma x}+V_{-}{e}^{+\gamma x}$$

• $V_{+}$：沿 +x 方向传播的波
• $V_{-}$：沿 −x 方向传播的波（反射波）,负载处因为匹配不反射(相当于无限长的电缆)，所以 没有反射波
• 只关心单向传播（从发送端向接收端），写作：
  $$V(x)=V_0{e}^{-\gamma x}$$

把$\gamma$分解：
$$\gamma =\alpha +j\beta$$
于是
$$V(x)=V_0{e}^{-\alpha x}{e}^{-j\beta x}$$

• $\alpha$ :$Np/m$（Neper per meter）是衰减常数（幅度随距離做指数衰减）,Neper奈珀和分贝一样，都是比率的对数表达式。分贝使用以10为底的对数，也就是十进制对数，而奈珀使用自然对数，也就是欧拉常数对数。
• $\beta$:$rad/m$是相位常数（表示波长/相位延迟）

这就是信号随距离呈指数衰减的本质原因。

2.衰减系数数特性

• 传输线的电报方程得出，衰减系数是频率的函数：

$$f(\omega )=>\gamma =\alpha +j\beta =\sqrt{(R+j\omega L)(G+j\omega C)}$$

• 其中：R每米串联电阻，L每米串联电感，G 每米并联电导，C 每米并联电容，$\omega =2\pi f$信号角频率

低频近似（ω → 0）

• 对低频信号，$\omega L\ll R$，$\omega C\ll G$
• γ 可近似为：

$$\gamma \approx \sqrt{RG}+j\cdot 0$$

• α 很小，主要由导体电阻 R 决定
• 低频信号几乎不衰减（万用表测不到）

高频近似（ω 较大）

• 高频时，$\omega L\gg R$，$\omega C\gg G$
• γ 可近似为：

$$\gamma \approx j\omega \sqrt{LC}+\frac{R}{2}\sqrt{\frac{C}{L}}+\frac{G}{2}\sqrt{\frac{L}{C}}$$

• 衰减常数 α ≈$\frac{R}{2}\sqrt{C/L}+\frac{G}{2}\sqrt{L/C}$
• 这时 α 会随频率变化（尤其 R 也随频率略增，C/G 对高频影响更明显）

高频信号衰减明显，低频信号几乎不衰减

损耗近似

• 特性阻抗：
  $$Z_0\approx \sqrt{\frac{L}{C}}$$
• 衰减常数近似为：
  $$\alpha \approx \frac{R}{2}\sqrt{\frac{C}{L}}+\frac{G}{2}\sqrt{\frac{L}{C}}=\frac{R}{2Z_0}+\frac{G{Z}_0}{2}$$

• 此公式直观地把衰减分成“导体损耗”（与 R成正比）和“介质损耗”（与G成正比）。

3.能量介质传播与指数衰减的关系

• 如果能量在吸收介质中传播（雾、水、大气强吸收段、土壤、组织），能量满足“比率损失 ∝ 当前能量”，产生 指数衰减：

$$\frac{dX}{dt}=-kX(t),k>0$$

$$X(t)=X_0{e}^{-kt}$$

• 像传输线方程这样的高阶常系数线性齐次微分方程，其通解也是多个指数函数的解的组合，能量的传播也满足指数衰减关系。

4.dB标度

• 工程上常用 dB/m 表示衰减。此时指数衰减在 dB 标度上变成了“线性衰减”。因此信号每增加一段距离，损耗的 dB 是恒定的，方便计算与叠加。

• 例如：

  • 光纤损耗：x dB/km
  • 声波吸收率： x dB/m
  • 传输线损耗：x dB/m

5.功率指数衰减

• 沿线的电压和电流幅度随距离 (x) 衰减：

$$V(x)=V_0{e}^{-\alpha x},I(x)=I_0{e}^{-\alpha x}$$

• 单位长度的瞬时功率为：

$$P(x)=\frac{1}{2}|V(x)|\cdot |I^{\ast }(x)|$$

• 代入衰减公式（幅度同样指数衰减）：

$$P(x)\propto V(x{)}^2\propto e^{-2\alpha x}$$

• 所以功率（能量传输速率）衰减指数更快。