在学习沐神的课时,对其中示例的代码部分进行详细分析和整理。
我们用 带噪声的正弦序列 做一个简单的 Python 示例,直观展示传统 AR 模型如何预测序列。
一、模型思路
自回归模型(AR) 假设当前值只依赖过去
τ
\tau
τ个时间点:
x
t
=
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
⋯
+
ϕ
τ
x
t
−
τ
+
ϵ
t
x_t = \phi_1x_{t-1}+\phi_2x_{t-2}+\cdots + \phi_{\tau}x_{t-\tau} +\epsilon_t
xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕτxt−τ+ϵt
其中,
τ
\tau
τ称为滞后阶数(lag),
ϵ
t
\epsilon_t
ϵt是噪声项,可以通过线性回归拟合系数
ϕ
1
,
…
,
ϕ
τ
\phi_1, \dots, \phi_\tau
ϕ1,…,ϕτ。
二、模拟数据
为了演示传统 AR 模型的序列预测,我们先生成一组模拟序列数据。按照下述方式生成的序列既有明显的周期趋势,又有一定的随机波动,非常适合用来演示自回归模型(AR)的预测能力。
-
序列类型:正弦函数 + 可加性噪声
-
公式:
x t = sin ( 0.01 ⋅ t ) + ϵ t , ϵ t ∼ N ( 0 , 0.2 ) x_t = \sin(0.01 \cdot t) + \epsilon_t, \epsilon_t \sim \mathcal{N}(0, 0.2) xt=sin(0.01⋅t)+ϵt,ϵt∼N(0,0.2) -
噪声说明: ϵ t \epsilon_t ϵt是均值为 0、标准差为 0.2 的高斯噪声,模拟现实序列中的观测误差或随机波动
-
时间步数: T = 1000 T = 1000 T=1000
0.01 ⋅ T = 0.01 × 1000 = 10 0.01 \cdot T = 0.01 \times 1000 = 10 0.01⋅T=0.01×1000=10(相当于 约 1.59 个正弦周期)
def gen_data(n_samples: int):
time = torch.arange(1, n_samples + 1, dtype=torch.float32) # 从1到1000
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (n_samples,))
return time, x
n_samples = 1000 # 总共产生1000个点
time, x = gen_data(n_samples)
我们将数据绘制出来:
def plot_data(time: torch.Tensor, data: torch.Tensor):
plt.figure(figsize=(12, 4))
plt.plot(time, x, label="带噪声正弦序列")
plt.xlabel("时间步")
plt.ylabel("值")
plt.title("模拟序列数据生成示例")
plt.legend()
plt.grid()
plt.show()
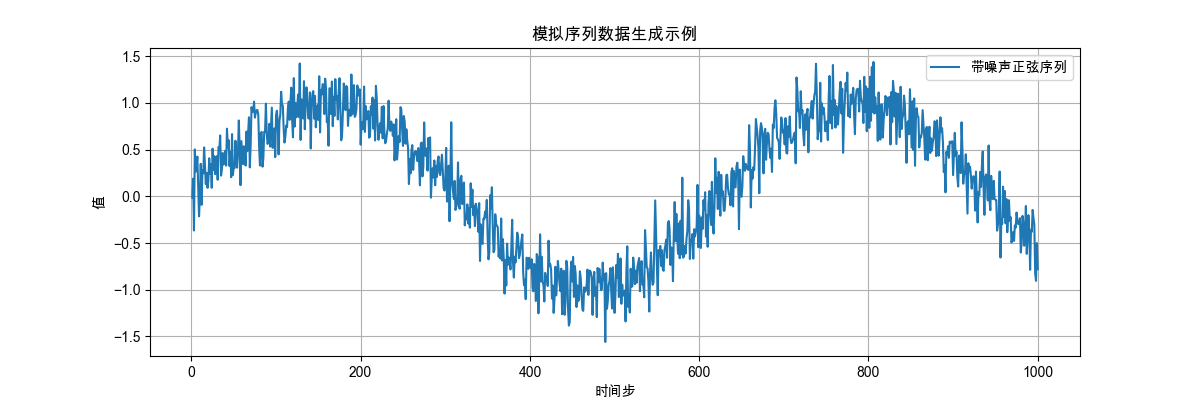
-
接下来,我们将这个序列转换为模型的特征-标签(feature-label)对。 基于嵌入维度,我们将数据映射为数据对 y t = x t y_t = x_t yt=xt和 x t = [ x t − τ , ⋯ , x t − 1 ] \mathbf{x}_t = [x_{t-\tau}, \cdots, x_{t-1}] xt=[xt−τ,⋯,xt−1]。 这比我们提供的数据样本少了 τ \tau τ个, 因为我们没有足够的历史记录来描述前 τ \tau τ个数据样本。 一个简单的解决办法是:如果拥有足够长的序列就丢弃这几项; 另一个方法是用零填充序列。
注意:我们这里的数据集用于单步预测,即给定过去连续 τ \tau τ个观测值,预测下一个时间点。特征数据均来自真实序列的观测值(每个样本都是由真实数据的连续 τ \tau τ个值组成,不包含模型的预测值),label也来自真实序列。
这里因为我们的样本数 n _ s a m p l e s = 1000 n\_samples = 1000 n_samples=1000,我们选择丢弃前 τ = 4 \tau=4 τ=4项。生成的数据对个数为 n _ s a m p l e s − τ = 996 n\_samples - \tau = 996 n_samples−τ=996。
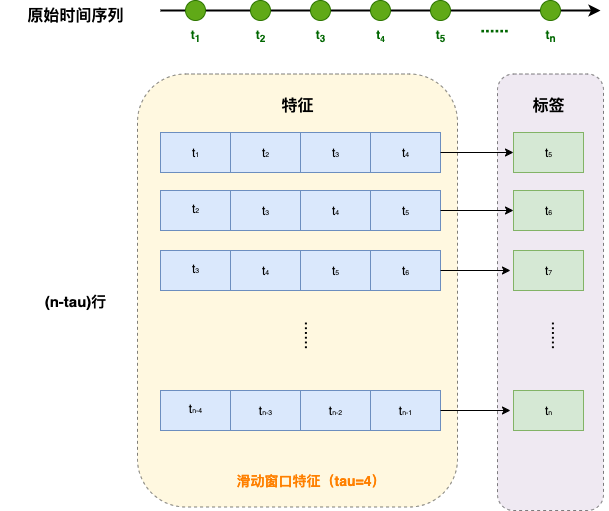
-
在这里,我们仅使用前 600 600 600个"特征-标签"对构成训练集,用于训练。
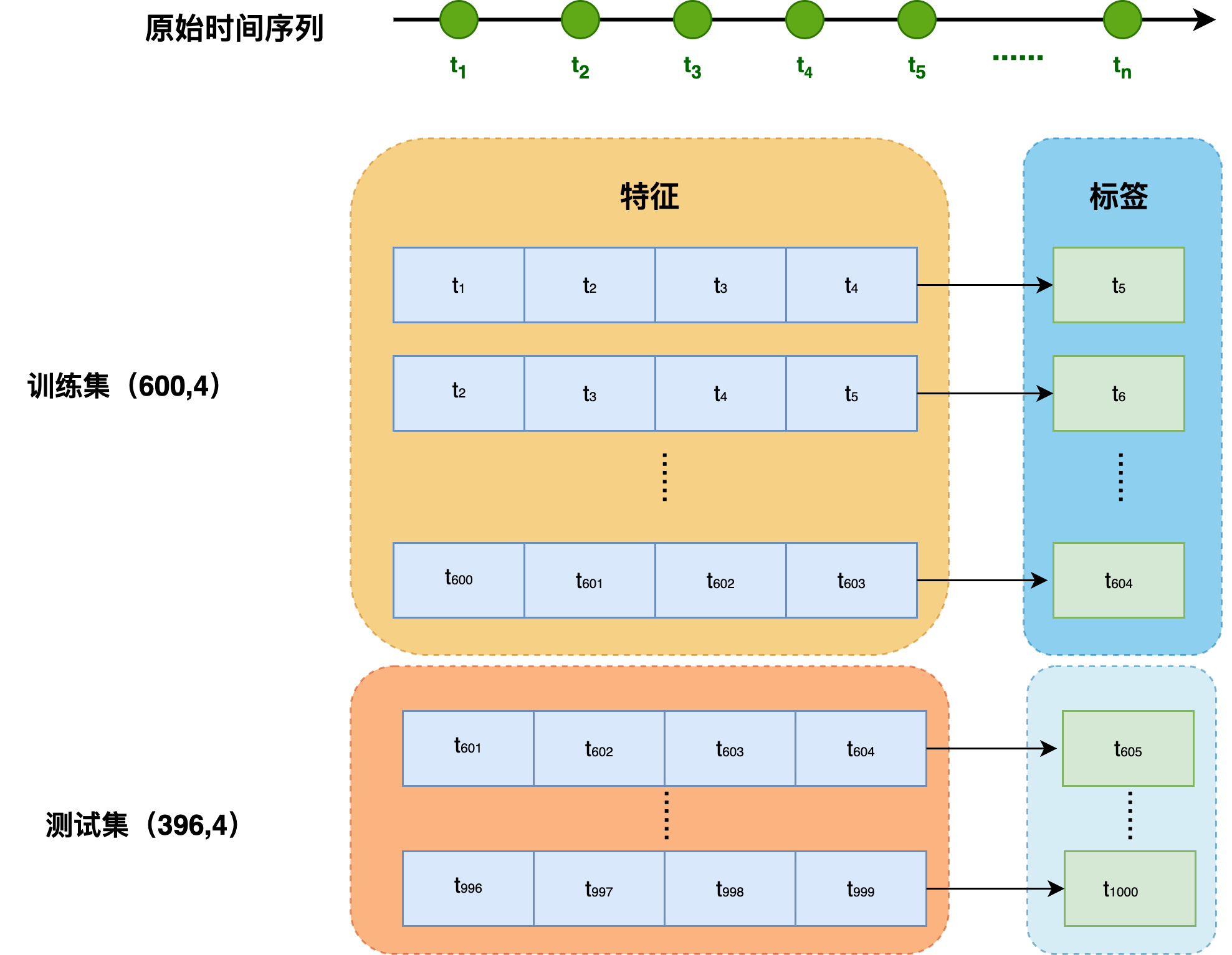
def create_ar_dataloader(x: torch.Tensor, tau: int, n_train: int, batch_size: int = 16):
"""
构建滑动窗口 AR 特征,并封装成 PyTorch DataLoader
Args:
x : torch.Tensor, 时间序列, shape (T,)
tau : int, 滞后阶数
n_train : int, 用于训练的样本数
batch_size : int, DataLoader batch size
Return:
train_loader : PyTorch DataLoader
test_loader : PyTorch DataLoader
features : torch.Tensor, 滑动窗口特征
labels : torch.Tensor, 对应标签
"""
T = x.shape[0]
# 构建滑动窗口特征
features = torch.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))
# 划分训练集和测试集
X_train = features[:n_train]
y_train = labels[:n_train]
X_test = features[n_train:]
y_test = labels[n_train:]
# 封装成 DataLoader
train_dataset = TensorDataset(X_train, y_train)
test_dataset = TensorDataset(X_test, y_test)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
return train_loader, test_loader, features, labels
这里我们假设 τ = 4 \tau = 4 τ=4, n t r a i n = 600 n_{train}=600 ntrain=600, b a t c h _ s i z e = 16 batch\_size = 16 batch_size=16
train_loader, test_loader, features, labels = create_ar_dataloader(x=x, tau=tau, n_train=n_train, batch_size=batch_size)
num_train_samples = len(train_loader.dataset)
num_test_samples = len(test_loader.dataset)
print(f"num train samples: {num_train_samples}, num test samples: {num_test_samples}")
输出:
num train samples: 600, num test samples: 396
三、MLP模型
在这里,我们使用一个相当简单的架构训练模型: 一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失。
-
网络权重初始化
torch.nn.init.xavier_uniform_实现的是:
W i j ∼ U ( − 6 n in + n out , 6 n in + n out ) W_{ij} \sim U\left( -\sqrt{\frac{6}{n_\text{in}+n_\text{out}}}, \; \sqrt{\frac{6}{n_\text{in}+n_\text{out}}} \right) Wij∼U(−nin+nout6,nin+nout6)
它包含以下优点:-
保持前向传播方差稳定
V a r [ y ] ≈ V a r [ x ] \mathrm{Var}[y] \approx \mathrm{Var}[x] Var[y]≈Var[x] -
保持反向传播梯度方差稳定
V a r [ δ x ] ≈ V a r [ δ y ] \mathrm{Var}[\delta_x] \approx \mathrm{Var}[\delta_y] Var[δx]≈Var[δy] -
避免梯度爆炸(variance 过大)
-
避免梯度消失(variance 过小)
-
对 Sigmoid / Tanh / GELU 这类激活函数尤其友好(原因:对称 + 缩放良好)
因此,它是最常见也最推荐的线性层初始化方法之一,并被广泛用于传统神经网络、RNN、Transformer 的 FFN 层等模块。
def init_weights(m): """ 初始化网络权重,使用这种初始化,训练更快收敛、更稳定 """ # 判断只对全连接层进行初始化 if isinstance(m, nn.Linear): nn.init.xavier_uniform_(m.weight) # 均匀分布采样初始化 if m.bias is not None: nn.init.zeros_(m.bias) # 偏置初始化为 0(推荐做法)- 为什么偏置用 0 初始化?
- 偏置不影响输入的方差传播
- 不引入额外的随机性
- 简洁、稳定、收敛更快
- 这是工业界通用做法(默认 bias=0 足够好)
-
-
模型定义
import torch.nn as nn class SimpleMLP(nn.Module): def __init__(self, input_dim=4, hidden_dim=10, output_dim=1): super().__init__() self.model = nn.Sequential( nn.Linear(input_dim, hidden_dim), nn.ReLU(), nn.Linear(hidden_dim, output_dim), ) self.apply(init_weights) def forward(self, x): return self.model(x) net = SimpleMLP(input_dim=tau, hidden_dim=hidden_dim, output_dim=1) -
损失函数
MSELoss计算平方误差时不带系数1/2
loss_fn = nn.MSELoss(reduction='none')注意:如果设定
reduction='none',该损失函数不会做任何 reduction(求和/求平均),所以返回的 loss 是“逐样本、逐元素”的张量,而不是一个标量。 -
优化器
在训练深度学习模型时,我们需要一个优化器来根据梯度更新参数。这里采用Adam优化器,其中需要指定学习率
lr。optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
四、模型训练
1. 训练模型
此外,在训练循环中,我们希望每个 epoch 统计一个平均损失,用于观察模型训练过程中的收敛情况。
- 在每个 epoch 中,我们遍历所有 mini-batch,计算每个 batch 的损失
- 将每个 batch 的损失按样本数累加,得到该 epoch 的总损失
- 最后除以总样本数,得到 每个样本的平均损失
2. code
def train(net, train_iter, loss_fn, optimizer, epochs, device=None):
"""
通用训练循环
Args:
- net: 待训练的神经网络(nn.Module)
- train_iter: DataLoader,提供 (X, y) 批数据
- loss_fn: 损失函数,例如 MSELoss(reduction='none')
- optimizer: 优化器,例如 Adam、SGD
- epochs: 训练轮数
- device: 指定设备,默认自动选择 GPU 或 CPU
"""
device = device or ('cuda' if torch.cuda.is_available() else 'cpu')
net = net.to(device)
# 总样本数,用于计算 epoch 平均损失
total_samples = len(train_iter.dataset)
for epoch in range(epochs):
net.train() # 切换到训练模式(启用 Dropout、BN 等)
total_loss = 0.0
# 遍历所有 mini-batch
for X, y in train_iter:
# 将数据移动到 GPU / CPU
X, y = X.to(device), y.to(device)
# 1. 前向传播
y_hat = net(X)
# 2. 计算损失
# 若使用 MSELoss(reduction='none'), 返回按样本的损失
# 因此需要对一个 batch 做 mean 得到标量
loss = loss_fn(y_hat, y).mean()
# 3. 反向传播之前清空梯度
# 防止梯度累积(PyTorch 默认不会自动清空)
optimizer.zero_grad()
# 4. 反向传播
loss.backward()
# 5. 更新参数
optimizer.step()
# 6. 累积损失,用于 epoch 统计
batch_size = X.size(0)
# 防止梯度回传影响累积计算
total_loss += loss.detach().item() * batch_size
# 计算该 epoch 的平均损失
avg_loss = total_loss / total_samples
print(f"Epoch {epoch + 1}/{epochs}, Loss = {avg_loss:.4f}")
print("Training finished!")
epochs = 5
device = 'cuda' if torch.cuda.is_available() else 'cpu'
train(net, train_loader, loss_fn, optimizer, epochs)
Epoch 1/5, Loss = 0.1360 Epoch 2/5, Loss = 0.0590 Epoch 3/5, Loss = 0.0584 Epoch 4/5, Loss = 0.0555 Epoch 5/5, Loss = 0.0541 Training finished!
从数值下降趋势可以看出模型训练逐步收敛。
五、模型预测
1. 单步模型预测
训练完成后,我们可以用训练好的模型对之前构造的完整序列数据(features)做单步预测(one-step prediction),并与原始数据对比。
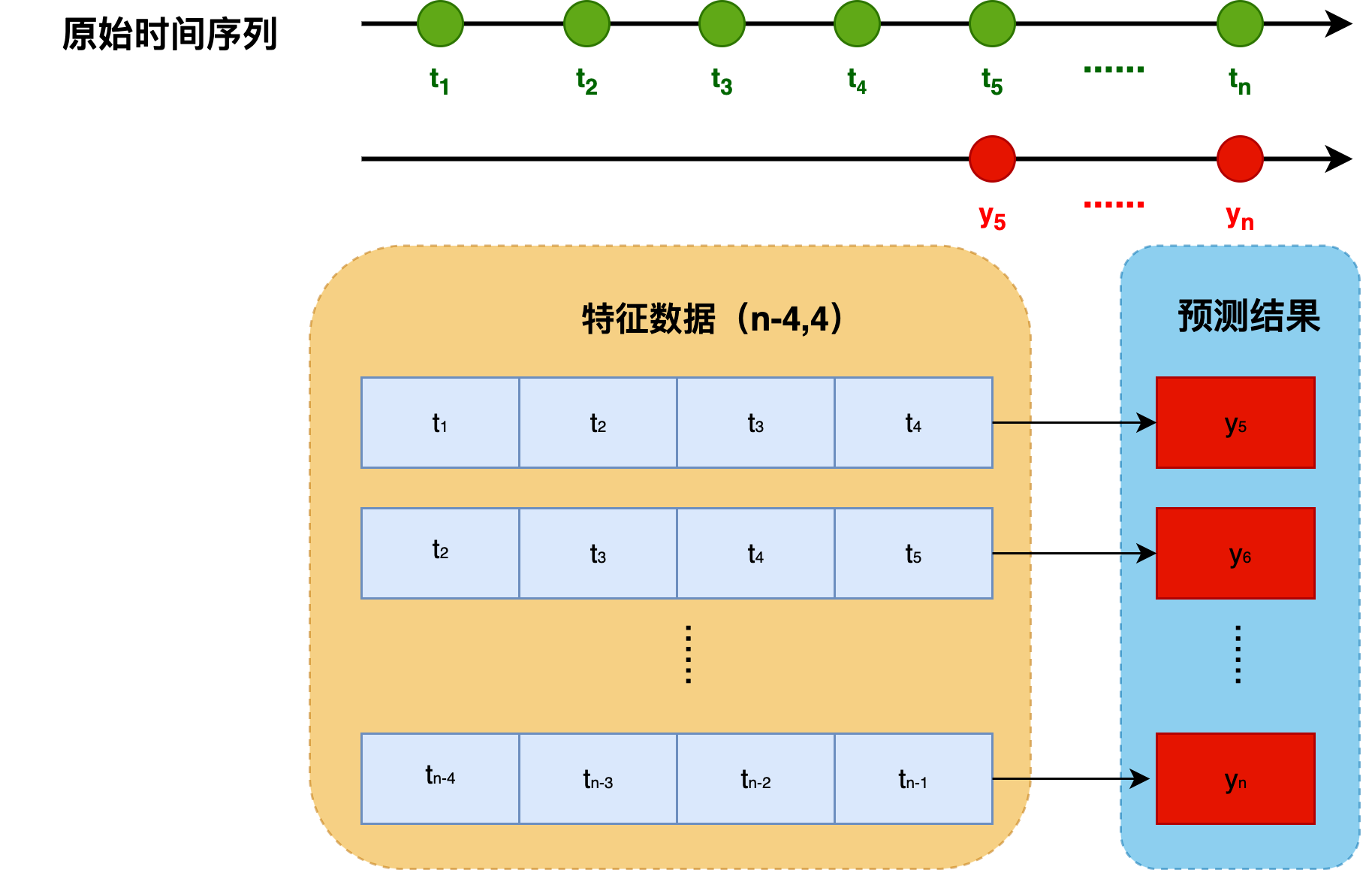
- 本质就是使用模型对完整的特征数据进行预测,即用 ( x i − 4 , x i − 3 , x i − 2 , x i − 1 ) (x_{i-4}, x_{i-3}, x_{i-2}, x_{i-1} ) (xi−4,xi−3,xi−2,xi−1)来预测 x i x_i xi的值,其中 i = 5 , 6 , ⋯ , 1000 i = 5, 6, \cdots, 1000 i=5,6,⋯,1000。
# 模型预测
net.eval() # 切换到评估模式
with torch.no_grad():
onestep_preds = net(features).detach().numpy()
-
构建时间轴,并对预测与原始序列进行对齐:
x_np = x.detach().numpy() # 构建时间轴 time_all = time.numpy() time_pred = time_all[tau:] # 预测时间轴,从 tau 开始这里我们构造了两条时间轴,其中
time_all是完整时间序列的时间戳,time_pred是预测标签对应的时间戳(因为我们的标签从x[tau]开始,所以时间轴会跳过前tau个) -
绘制预测效果
def plot_one_step_prediction(x: torch.Tensor, onestep_preds: torch.Tensor, time: torch.Tensor, tau: int, title: str = "One-Step Prediction", figsize=(8, 4)): """ 绘制模型的一步预测效果,与原始序列对比 Args: x : torch.Tensor, 原始时间序列 onestep_preds : torch.Tensor, 预测序列 time : torch.Tensor, 时间轴 tau : int, 滞后阶数 title : str, 图标题 figsize : tuple, 图大小 """ x_np = x.detach().numpy() # 构建时间轴 time_all = time.numpy() time_pred = time_all[tau:] # 预测时间轴,从 tau 开始 # 绘图 plt.figure(figsize=figsize) plt.plot(time_all, x_np, label='Original data') # 原始数据 plt.plot(time_pred, onestep_preds, label='1-step preds') # 模型预测 plt.xlabel('Time') plt.ylabel('x') plt.title(title) plt.legend() plt.xlim([time_all[0], time_all[-1]]) plt.show() plot_one_step_prediction(x, onestep_preds, time, tau=tau) 用蓝色线表示原始数据对,橙色线表示单步预测的结果。
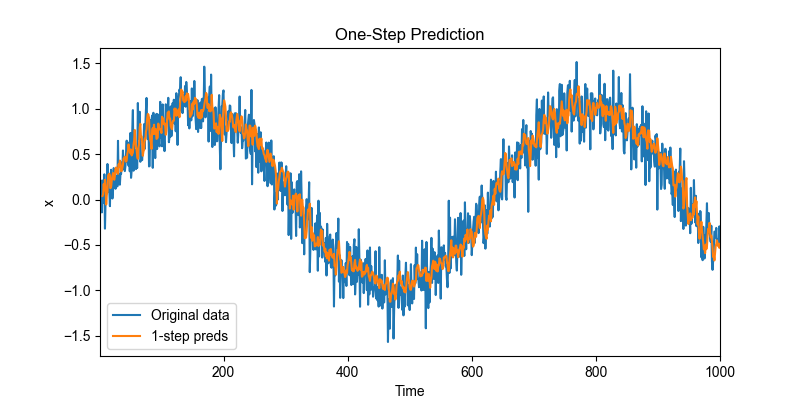
本实验的单步预测表现稳定且可靠。其关键原因在于:模型在预测阶段仍然能够使用完整的真实历史观测值作为输入特征。因此,即使预测时间步已经超出训练样本的范围(例如
n_train + tau = 600 + 4 = 604),模型的输入仍然来自真实序列,而非迭代生成的预测值。这避免了多步预测中常见的误差累积现象,使得模型的预测结果在训练范围之外依旧保持平滑、合理且具有可信性。
2. 多步模型预测
-
在前面的单步预测(one-step prediction)实验中,我们的目标是利用最近的真实观测来预测下一时刻的值:
x ^ t = f ( x t − τ , x t − τ + 1 , ⋯ , x t − 1 ) \hat{x}_t = f(x_{t-\tau}, x_{t-\tau+1}, \cdots, x_{t-1}) x^t=f(xt−τ,xt−τ+1,⋯,xt−1)
这种方式的关键特征是: 输入窗口始终来自真实序列,不包含任何模型自己生成的预测值。因此,单步预测通常非常稳定,也不会产生误差累积。
-
如果希望预测未来多个时间步,我们将不可避免地使用模型自己生成的预测来继续往前预测。
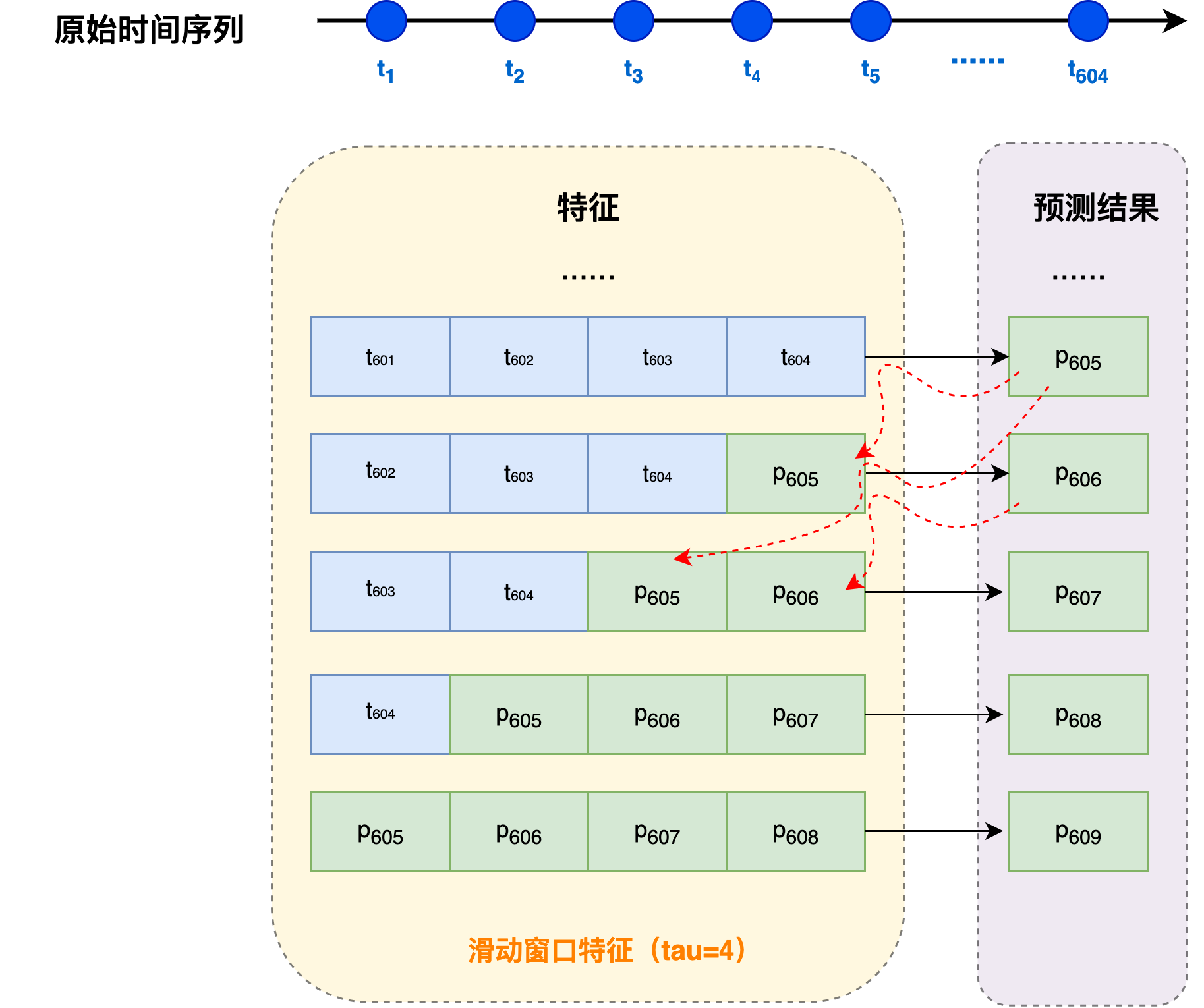
假设观测序列已知到 x 604 x_{604} x604,预测过程如下:
x ^ 605 = f ( x 601 , x 602 , x 603 , x 604 ) , x ^ 606 = f ( x 602 , x 603 , x 604 , x ^ 605 ) , x ^ 607 = f ( x 603 , x 604 , x ^ 605 , x ^ 606 ) , x ^ 608 = f ( x 604 , x ^ 605 , x ^ 606 , x ^ 607 ) , x ^ 609 = f ( x ^ 605 , x ^ 606 , x ^ 607 , x ^ 608 ) , … \begin{align*} \hat{\boldsymbol{x}}_{605} &= \boldsymbol{f}(\boldsymbol{x}_{601}, \boldsymbol{x}_{602}, \boldsymbol{x}_{603}, \boldsymbol{x}_{604}), \\ \hat{\boldsymbol{x}}_{606} &= \boldsymbol{f}(\boldsymbol{x}_{602}, \boldsymbol{x}_{603}, \boldsymbol{x}_{604}, \hat{\boldsymbol{x}}_{605}), \\ \hat{\boldsymbol{x}}_{607} &= \boldsymbol{f}(\boldsymbol{x}_{603}, \boldsymbol{x}_{604}, \hat{\boldsymbol{x}}_{605}, \hat{\boldsymbol{x}}_{606}), \\ \hat{\boldsymbol{x}}_{608} &= \boldsymbol{f}(\boldsymbol{x}_{604}, \hat{\boldsymbol{x}}_{605}, \hat{\boldsymbol{x}}_{606}, \hat{\boldsymbol{x}}_{607}), \\ \hat{\boldsymbol{x}}_{609} &= \boldsymbol{f}(\hat{\boldsymbol{x}}_{605}, \hat{\boldsymbol{x}}_{606}, \hat{\boldsymbol{x}}_{607}, \hat{\boldsymbol{x}}_{608}), \\ &\dots \end{align*} x^605x^606x^607x^608x^609=f(x601,x602,x603,x604),=f(x602,x603,x604,x^605),=f(x603,x604,x^605,x^606),=f(x604,x^605,x^606,x^607),=f(x^605,x^606,x^607,x^608),…
其中,每一步预测的输入除了最近的真实观测,还需要使用前面预测的结果。此外,每一个新的预测值都会作为下一个输入的一部分。预测越远,误差越可能累积。 这里, x ^ 604 + k \hat{x}_{604+k} x^604+k 即为 k 步预测(k-step-ahead prediction),当 k = 1 k=1 k=1时,表示预测1个时间步后的值;当 k = 16 k=16 k=16时,表示预测16个时间步后的值。
⚠️ 注意:随着预测步数增加,误差可能会累积,因此多步预测通常比单步预测更难。
-
多步预测序列初始化:
在多步预测(multi-step prediction)中,我们需要一步步向前预测未来的时间步。为了方便后续迭代计算,我们通常会先初始化整个预测序列:
multistep_preds = torch.zeros(n_samples) multistep_preds[: n_train + tau] = x[: n_train + tau] # 保留训练和初始窗口数据 其中,前
n_train + tau( 600 + 4 = 604 600 + 4=604 600+4=604) 个时间步使用真实观测值填充,这样能保留历史观测数据,确保模型一开始的输入窗口是完全真实的,为后续预测提供初始输入。 -
多步预测
在多步预测(multi-step prediction)中,我们从训练数据的末尾(
n_train+tau)开始,一步步向前生成未来时间步的预测值。for i in range(n_train + tau, n_samples): # 使用前 tau 个值(可能包括预测值)作为输入 input_window = multistep_preds[i - tau:i].reshape(1, -1) multistep_preds[i] = net(input_window)每一步都使用当前窗口的 τ \tau τ个数值作为输入;如果窗口中包含预测值,那么后续预测将基于这些预测。
-
绘图展示
我们对可视化原始序列、单步预测和多步预测进行对比,可以直观理解模型的预测效果以及随时间累积误差的情况。
-
原始序列,对应整个时间轴 ,图例中对应蓝色
-
单步预测序列:从
tau开始,因为它使用前 tau 个值预测下一步,图例中对应橙色使用全部真实历史,因此误差小。
-
多步预测序列:从
n_train + tau开始,因为多步预测依赖训练数据结束后的预测值,图例中对应红色误差随时间可能累积
def compare_single_and_multi_steps_predictions( x: torch.Tensor, time: torch.Tensor, onestep_preds: torch.Tensor, multistep_preds: torch.Tensor, tau: int, n_train: int, title: str = "One-Step VS Multi-Step Prediction", figsize=(8, 4)): """ 可视化单步预测和多步预测结果 Args: x : 原始序列, shape (T,) time : 时间序列, shape (T,) onestep_preds : 单步预测结果, shape (T-tau,) multistep_preds: 多步预测序列, shape (T,) tau : 滞后阶数 n_train : 训练样本数 title : 图表标题 figsize : 图表大小 """ # 转成 numpy 方便绘图 x_np = x.detach().numpy() onestep_preds_np = onestep_preds.detach().numpy() multistep_preds_np = multistep_preds.detach().numpy() # 构建时间轴 time_all = time.numpy() time_pred = time_all[tau:] # 单步预测时间轴 time_multistep = time_all[n_train + tau:] # 多步预测时间轴 plt.figure(figsize=figsize) # 原始数据 plt.plot(time_all, x_np, label='Original data', color='blue') # 单步预测 plt.plot(time_pred, onestep_preds_np, label='1-step preds', linestyle='--', color='orange') # 多步预测 plt.plot(time_multistep, multistep_preds_np[n_train + tau:], label='multi-step preds', color='red', linestyle='-.') plt.xlabel('Time') plt.ylabel('x') plt.title(title) plt.legend() plt.xlim([time_all[0], time_all[-1]]) plt.show() -
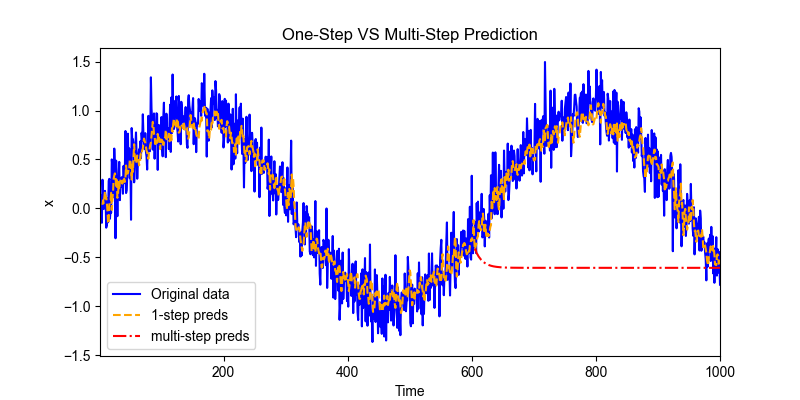
如上例所示,**多步预测(红色线)**在短时间内就逐渐偏离真实序列,最后甚至收敛到某个几乎不再变化的常数。这是一种非常典型的现象,在自回归模型(AR)、RNN、甚至 Transformer 的文本生成中都会出现。
为什么会出现这种现象呢?关键原因是误差累积(error accumulation):
- 在多步预测中,每一步预测的输入不仅包含真实观测值,还可能包含前一步预测产生的误差。
- 假设在第 t + 1 t+1 t+1步预测中累积了一些误差,那么这个扰动会直接影响第 t + 2 t+2 t+2步的预测输入。
- 随着步骤推进,误差逐步累积并按序传递,最终导致预测值偏离真实观测,甚至趋向常数。
这也解释了为什么短期预测通常比较准确,例如未来几个小时的天气预报,而超过一定时间跨度后,预测精度会迅速下降。
3. 不同k-step预测
为了更直观展示多步预测的误差累积现象,我们构建一个 features 矩阵,用来同时存储:
-
前
tau个时间步使用真实观测值(作为滑动窗口输入) -
后
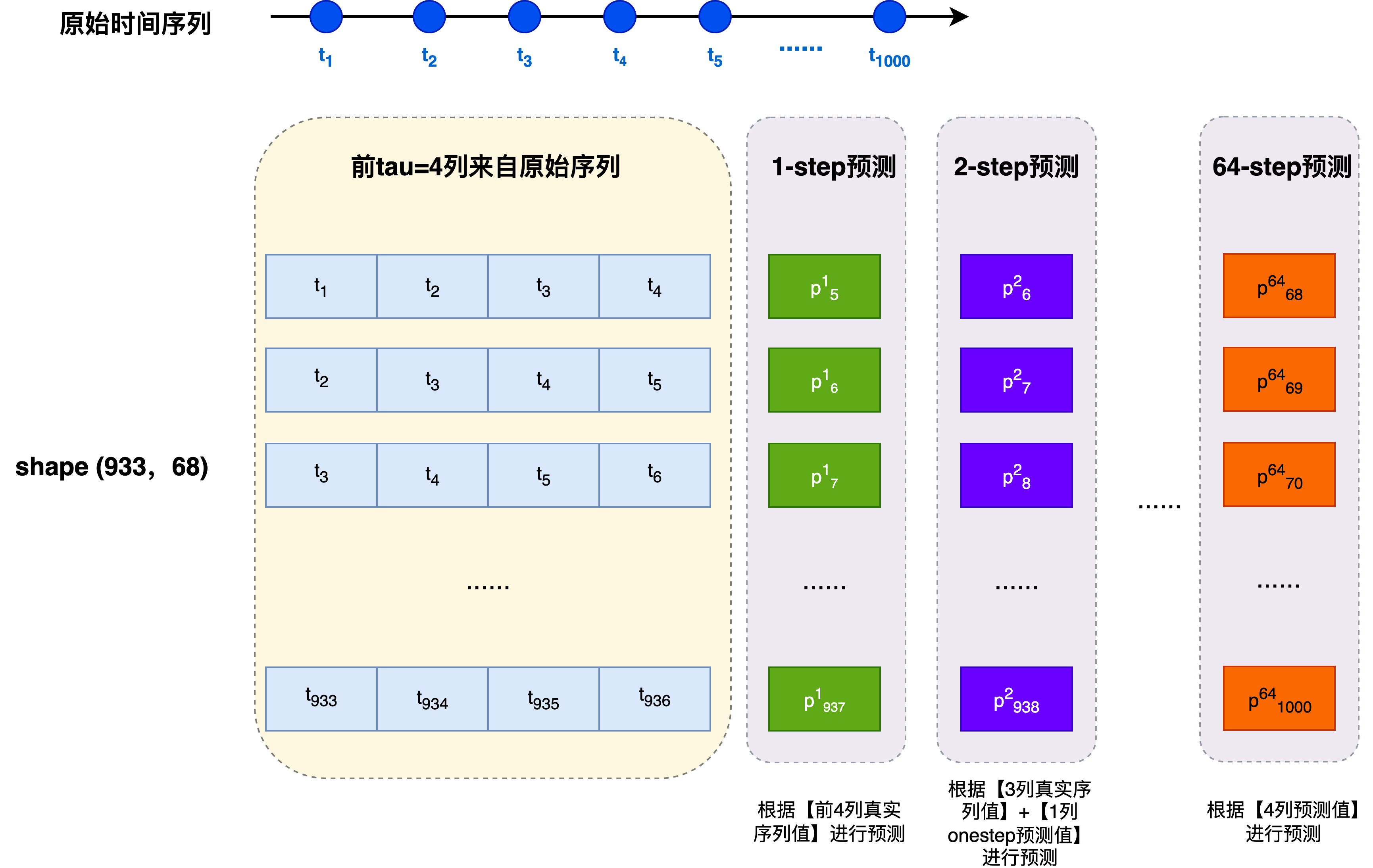
max_steps列的模型预测结果(1-step, 2-step, …, max_steps-step)features = torch.zeros((n_samples - tau - max_steps + 1, tau + max_steps)) # 前tau列作为观测值 for i in range(tau): features[:, i] = x[i: i + n_samples - tau - max_steps + 1] # 后 max_steps 列依次存 1-step, 2-step ... max_steps-step 预测 for i in range(tau, tau + max_steps): # 每列预测都基于前 tau 列 input_window = features[:, i - tau:i] features[:, i] = net(input_window).reshape(-1)-
每行表示一个滑动窗口样本
-
前
tau列:真实观测窗口,这 τ \tau τ列来自原始序列样本索引 features(长度 tau) 0 [0, 1, 2, 3] 1 [1, 2, 3, 4] 2 [2, 3, 4, 5] 3 [3, 4, 5, 6] 4 [4, 5, 6, 7] 每一行就是一个训练样本(特征向量),用于预测下一个值或做多步预测
-
后
max_steps列依次存放1-step、2-step、…、max_steps的预测值;每一列都依赖于前面 τ \tau τ列数据,其中可能包含预测值,因此会出现误差累积。
-
第 τ = 4 \tau=4 τ=4列存放模型的1-step预测
使用 [ x 1 , x 2 , x 3 , x 4 ] [x_1, x_{2}, x_{3}, x_{4}] [x1,x2,x3,x4]预测 x 5 x_{5} x5
-
第 τ + 1 = 5 \tau+1= 5 τ+1=5列存放模型的2-step预测
使用 [ x 2 , x 3 , x 4 , x ^ 5 ] [x_{2}, x_{3}, x_{4}, \hat{x}_{5}] [x2,x3,x4,x^5]预测 x 6 x_{6} x6
-
第 τ + m a x _ s t e p s = 68 \tau + max\_steps = 68 τ+max_steps=68列存放模型的64-step预测
使用 [ x ^ 64 , x ^ 65 , x ^ 66 , x ^ 67 ] [\hat{x}_{64}, \hat{x}_{65}, \hat{x}_{66}, \hat{x}_{67}] [x^64,x^65,x^66,x^67]预测 x 68 x_{68} x68
列越靠后,对应的 k-step 预测步数越大,误差累积也可能越明显。
-
-
-
可视化
可视化模型在不同步长下的预测效果,包括 1-step、4-step、16-step 和 64-step 预测,并与原始序列进行对比,帮助理解多步预测中误差累积的现象。
steps = [1, 4, 16, 64] # 绘制不同 k-step 预测 line_styles = ['--', '-.', ':', '-'] # 为每条 k-step 曲线指定不同的线型 plt.figure(figsize=figsize) for i, k in enumerate(steps): idx = tau + k - 1 plt.plot( time[tau + k - 1: n_samples - max_steps + k], features[:, idx].detach().numpy(), label=f'{k}-step preds', linestyle=line_styles[i % len(line_styles)], # 循环使用线型 color=None # 可以保持自动配色,也可以指定 color ) # 原始序列 plt.plot(time, x.detach().numpy(), label='Original data', color='k', alpha=0.5) plt.xlabel('Time') plt.ylabel('x') plt.title('Different k-step Predictions') plt.legend() plt.xlim([time[0], time[-1]]) plt.show()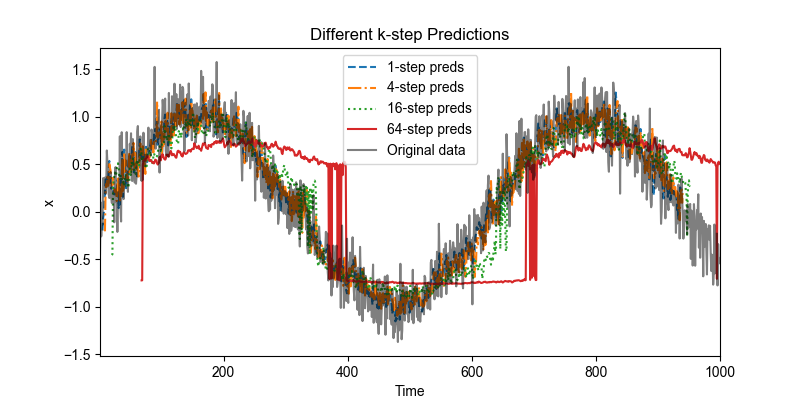
以上例子清楚地说明了预测步长对预测质量的影响:
- 对于较短步长的预测(如 1-step 或 4-step),模型仍能较好地捕捉序列的变化趋势,因此预测结果相对准确。
- 随着步长增加(如 16-step 或 64-step),每一步预测都依赖于前面预测的结果,误差逐步累积,导致预测值逐渐偏离真实序列。
- 结果表现为多步预测曲线迅速衰减或趋向常数,几乎无法反映真实序列的波动,因此对于远期预测而言,模型的输出几乎无实际参考价值。
这个现象直观地说明了多步预测的困难:短期预测可行,但长期预测通常会受到误差累积的严重影响。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








