【深度学习】Hidden vs Latent：神经网络与概率模型中两个“隐”的本质区别

为什么在学习神经网络与概率模型时，hidden 和 latent 总是被混用？
因为它们都翻译成“隐”，却来自完全不同的建模范式。

一、引言

1. 先说结论

• Hidden：
  • 神经网络里的中间表示
  • 确定性、可直接计算
  • 每一次前向传播都“真实存在”
• Latent：
  • 概率模型里的未观测随机变量
  • 不确定、需要推断
  • 只通过后验分布被“估计”

Hidden 是计算出来的；Latent 是推断出来的。

2. 概念对照表（避免混淆）

维度	Hidden	Latent
所属范式	神经网络	概率模型
是否随机	❌ 否（确定性）	✅ 是（随机变量）
是否可直接求值	✅ 前向传播即可	❌ 需做推断
是否显式建模分布	❌ 不需要	✅ 必须
典型例子	RNN 的 $h_t$、Transformer 的中间层	VAE 的 $z$、HMM 的隐状态
直觉比喻	盒子里真实存在的物品	潜在性格/动机等因素

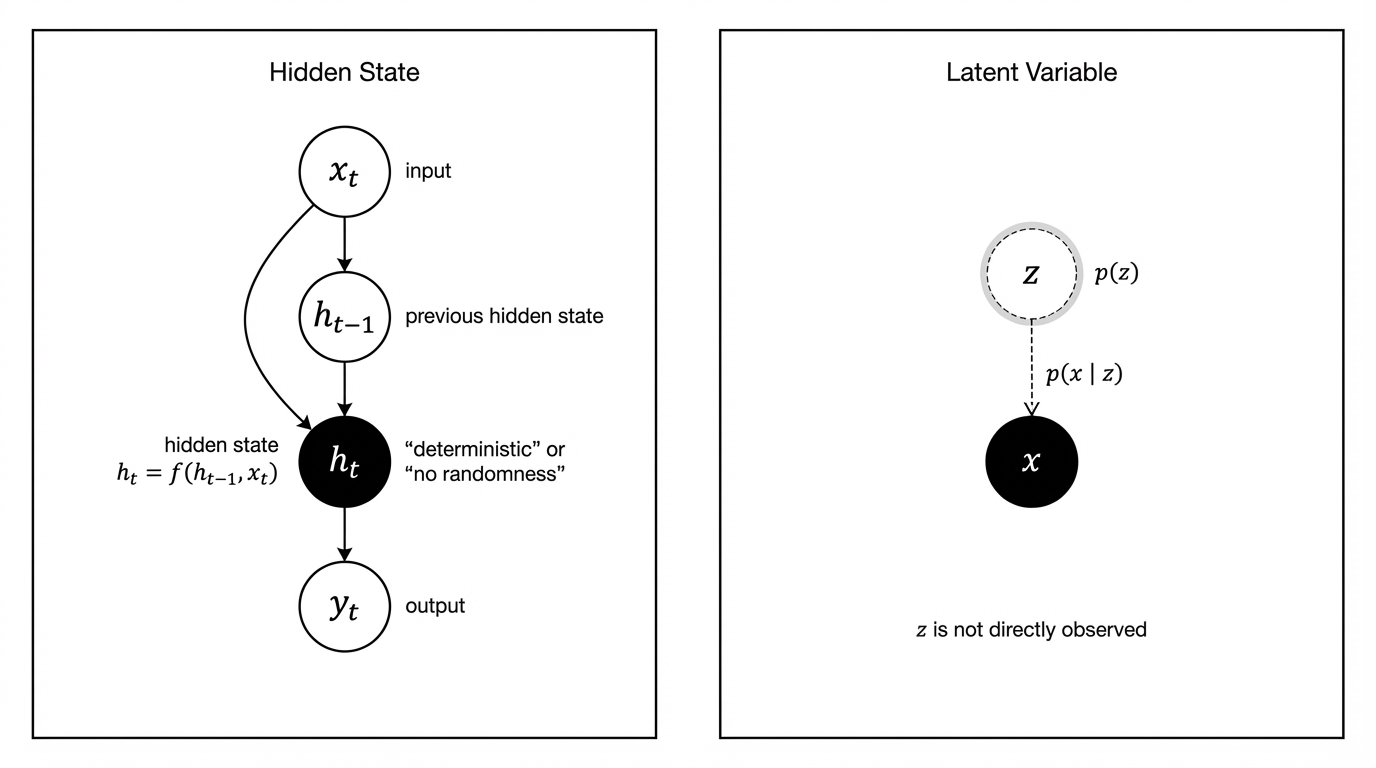
二、Hidden：网络结构中的隐藏状态

盒子里真实存在的一个物品，只是你没打开看到。

1. 词源直觉

• hidden 来自古英语 hide：遮住、藏起
• 含义强调：
  • 东西已经存在
  • 只是对观察者不可见

这与神经网络中的 hidden state / hidden layer 非常贴合。

2. 数学本质

​ Hidden 是确定性计算图上的节点：
$${\mathbf{h}}_t=f({\mathbf{h}}_{t-1},{\mathbf{x}}_t;\theta )$$

• 给定参数 $\theta$ 和输入 ${\mathbf{x}}_t$
• ${\mathbf{h}}_t$ 的值是唯一确定的
• 不涉及概率、不涉及采样

3. 关键特征总结

• 是模型内部真实存在的数据
• 每一步 forward 都会产生
• 反向传播可直接计算梯度
• 本质是 feature / representation

Hidden ≈ 网络在“此刻学到了什么表征”

三、Latent：概率模型中的隐变量

“这个人可能有某种性格特质”，但你没有观测，只能推断。

1. 词源直觉

• latent 来自拉丁语 latēre：潜伏、尚未显露
• 不是“被挡住”，而是：
  • 可能存在
  • 不可直接接触

强调的是：潜在因素（underlying factors）

2. 数学本质

​ Latent 是随机变量：
$$\begin{gathered} z\sim p(z) \\ x\sim p(x|z) \end{gathered}$$

• $z$ 本身不可观测
• 我们只能通过：$p(z|x)$来推断它的分布

3. 关键特征总结

• 不直接可见
• 不是一个确定数值
• 通常需要：
  • EM
  • 变分推断（VAE）
  • MCMC

Latent ≈ “是什么潜在原因生成了这些观测？”

四、为什么它们经常被混用？

1. 语言层面的原因

• 中文都翻译为“隐”
• 英文都带有 hidden / latent

2. 模型层面的交叉

一些模型同时出现两者：

• VAE：
  • Encoder 输出是 hidden representation
  • 但它参数化的是 latent 的分布
• Deep State Space Model：
  • hidden network
  • latent stochastic state

表面都在“中间层”，但数学地位完全不同。

五、判断口诀（非常实用）

1. 能不能前向一步直接算出来？

这是区分 计算节点 和 推断变量 的最快方法。

• 能 → Hidden

  hidden 属于计算图中的节点，给定输入与参数，一次 forward 即可得到唯一确定的数值，本质是模型在计算过程中形成的中间特征表示。

• 不能，必须算 posterior → Latent

  latent 属于概率模型中的随机变量，不是函数输出，必须通过条件分布（posterior）进行推断。

2.是不是显式写了 $p(\cdot )$？

这是一个形式层面的硬判断，不看直觉，只看模型在数学建模阶段写了什么。

​ 显式的意思是数学建模阶段是否为某个变量定义了概率分布。

• 是 → Latent

  ​ latent 变量以随机变量的形式出现，并被显式建模分布，例如：$z\sim p(z),x\sim p(x|z)$，其中$z$不是通过计算得到的，而是被假设存在、需要通过观测进行推断的潜在因素。

• 否 → Hidden

  ​ hidden 是确定性的中间表示，仅以函数形式出现：$h=f(x;\theta )$，给定输入和参数，$h$的值唯一确定，不涉及概率建模。

• 只要你为一个变量建模了分布，它就不再是 hidden，而是 latent。

• Hidden 用函数表示；Latent 用概率分布表示。

六、总结

• Hidden 是网络结构中的确定性中间表示
• Latent 是概率模型中用于解释数据生成过程的随机变量

它们的“隐”，一个是“被遮住的已知”，一个是“尚未显露的未知”。