57.零钱兑换II

一、题目描述

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

• 提示：

  1 <= coins.length <= 300
  1 <= coins[i] <= 5000
  coins 中的所有值 互不相同
  0 <= amount <= 5000

二、解题思路

（动态规划第十三题）

通过题目可以知道，这是一道需要计算的选取硬币的组合数，与54_目标和问题类似，是一道求组合数的问题，题中说了每一种面额的硬币数假设是无线的，可以看做是一个完全背包问题。

动规五部曲:

第一步：确定dp数组以及下标的含义

dp[j]表示金额之和等于j的硬币组合数

第二步：确定递推公式

对于面额为 coin 的硬币，当coin ≤ j ≤ amount 时，如果存在一种硬币组合的金额之和等于 j−coin，则在该硬币组合中增加一个面额为 coin 的硬币，即可得到一种金额之和等于 j 的硬币组合。因此需要遍历 coins，对于其中的每一种面额的硬币，更新数组dp 中的每个大于或等于该面额的元素的值。既然要求的是达到所要求的的组合数，那么要得到当前金额之和等于j的组合数dp[j]，当面临某一个硬币coin[i]时，有两种决策，这两种决策决定了两种组合方式，就是选或者不选coins[i]:

• 当不选择coins[i]时，此时已选硬币的金额之和应该是j-coins，对应的组合数应该是dp[j-coins]
• 当选择coins[i]时，此时已选硬币的金额之和就是j，对应额组合数就是dp[j]

所以总的组合数就为：dp[i] = dp[i] + dp[j-coins[i]]

第三步：dp数组如何初始化

初始化的边界是dp[0] = 1，只有当不选取任何硬币的时候，金额之和才为0，因此只有一种硬币组合。

第四部：确定遍历顺序

本题中我们是外层for循环遍历物品（钱币），内层for遍历背包（⾦钱总额），还是外层for遍历背包

（⾦钱总额），内层for循环遍历物品（钱币）呢？

答案是不行的！下面就来分析一下：

本题和纯完全背包是不一样的，纯完全背包是能否凑成总金额，而本题是要求凑成总金额的方式个数。题目中要求的是组合数，为什么强调是组合数呢？

例如：

5 = 2 + 2 + 1
5 = 2 + 1 + 2

这是一种组合问题，都是2 2 1。如果是排列数，上面就是两种排列了。组合不强调元素之间的顺序，排列强调元素之间的顺序。

因为纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也⾏，没有顺

序也⾏！对于本题中我们先来看看外层for循环遍历物品（钱币），内层for遍历背包（⾦钱总额）的情况。

for (int i = 0; i < coins.length; i++) { // 遍历物品
    for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] += dp[j - coins[i]];
    }
}

假设：coins[0] = 1，coins[1] = 5。

那么就是先把1加⼊计算，然后再把5加⼊计算，得到的⽅法数量只有{1, 5}这种情况。⽽不会出现{5, 1}

的情况。因为限制了1,5的顺序，到了i=5之后不可能会发生5,1的情况产生。所以这种遍历顺序中dp[j]⾥计算的是组合数！

假设下面将循环遍历的顺序变一下呢？

for (int j = 0; j <= amount; j++) { // 遍历背包容量
    for (int i = 0; i < coins.length; i++) { // 遍历物品
        if (j - coins[i] >= 0){
            dp[j] += dp[j - coins[i]]；
        }
    }
}

对于背包中的每一个值，都是经过1和5计算的，包含了{1,5}和{5,1}两种情况，会导致重复冗余的问题。

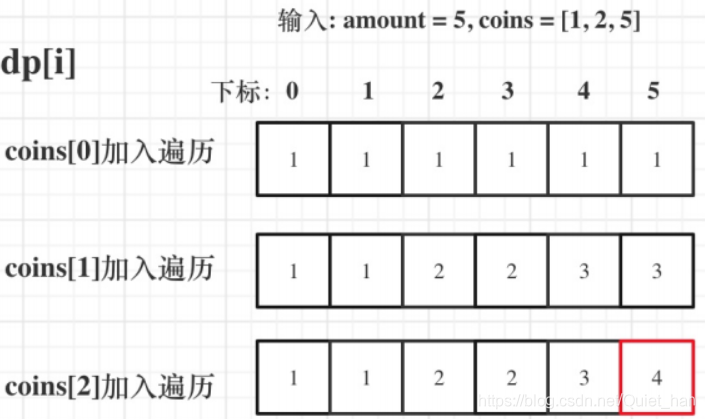
第五步：举例推导dp数组

输⼊: amount = 5, coins = [1, 2, 5] ，dp状态图如下：

三、代码演示

class Solution {
    public int change(int amount, int[] coins) {
        //定义dp数组
        int[] dp = new int[amount+1];

        //dp初始化
        dp[0] = 1;

        //遍历
        for(int i=0; i<coins.length; i++){
            for(int j=coins[i]; j<=amount; j++){
                dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

四、总结

对于求装满背包有几种方案的时候，认清遍历顺序是非常关键的：

• 如果求组合数就是外层for循环遍历物品，内层for遍历背包。

• 如果求排列数就是外层for遍历背包，内层for循环遍历物品。