一、向量的点乘
1、点乘的计算公式
=
其中 表示的是向量a的模即长度,
为向量a与向量b形成的夹角
2、点乘的矩阵表示
=
=
3、应用
(1) 计算两个向量之间的夹角,如下:
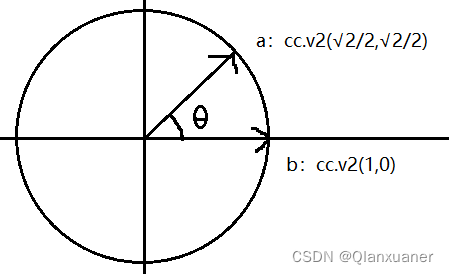
=
=
=
=
,得出
为45度
在cocosCreator中,
情况1:已知两个向量,求夹角:
let v1 = cc.v2(0 , 100);
let v2 = cc.v2(100 , 0);
let s1 = v1.signAngle(v2); //逆时针是正,顺时针是负
let s2 = s1 * 180 / (Math.PI); //将弧度转成角度
情况2:已知一个向量和要旋转的角度,求另一个向量:
let v3 = cc.v2(0 , 100);
let angle = 90; //要旋转的角度
let hudu = angle * Math.PI / 180; //将角度转成弧度
let r4 = v3.rotate(hudu); //rotate方法中的参数,正数表示逆时针,负数表示顺时针
(2)向量b在a上的投影,可以将力进行分解
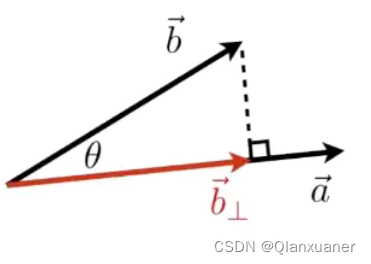
结论:最后红线部分的长度 =
(3) 判断两个向量是否接近或者方向相同
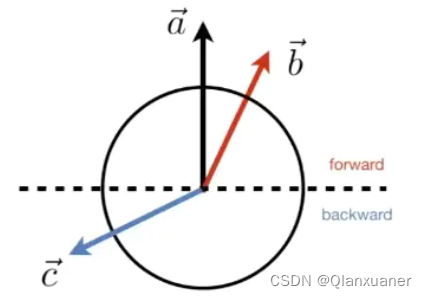
结论:
> 0,方向相同,越趋近1,越近
< 0,方向相反,越趋近-1,越远
二、向量叉乘
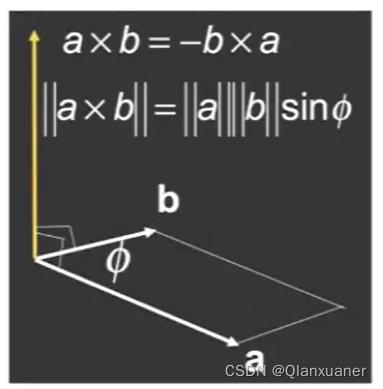
1、叉乘的定义:向量a叉乘向量b得到向量c,向量c垂直于向量a、b所形成的平面,方向由右手螺旋定则决定。
,即伸出右手,四个手指初始放在向量a的位置,然后四个手指向手心往向量b的方向收缩,得到大拇指的方向就是向量c的方向。
叉乘的计算公式: =
特殊:
=
,根据叉乘的计算公式,向量自己的叉乘得到的是零向量。
2、叉乘的矩阵表示
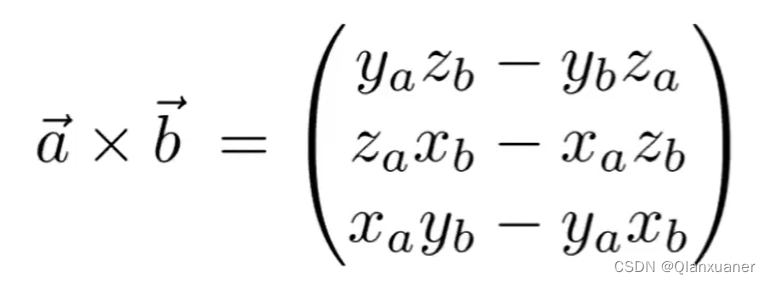
3、应用
(1)判断一个向量在另一个向量的左侧还是右侧
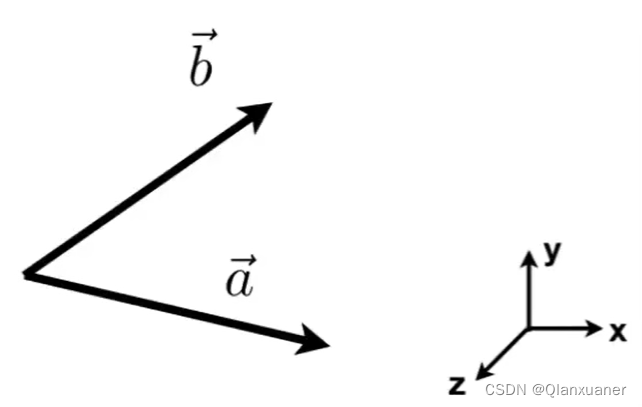
根据三维坐标系和右手螺旋定则得到 后的向量垂直向上,说明
在
的左侧,反过来,
在
的右侧。
(2)判断一个点是否在三角形内,可用于图形光栅化时候的采样,该点是否该被选取为像素点。
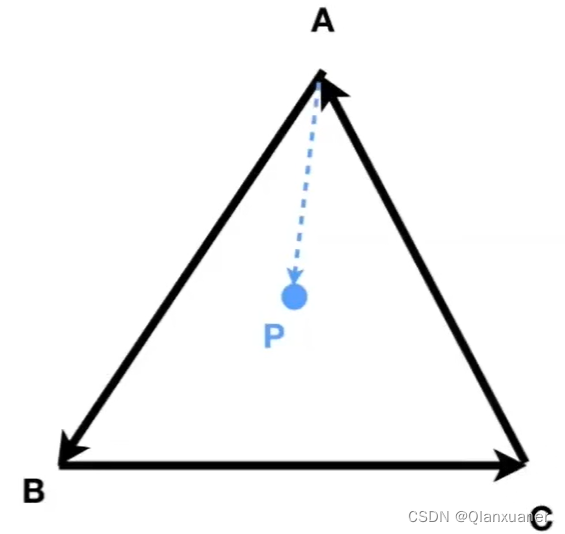
> 0
> 0
> 0
三角形的三条边和点P形成的向量进行叉乘后都大于0,说明点P是在三角形ABC内。





 本文深入探讨了向量的点乘和叉乘概念,包括计算公式、矩阵表示及实际应用。点乘用于计算向量夹角、投影和判断方向一致性;叉乘涉及判断向量方位、确定点在平面位置。通过实例展示了在游戏开发(如CocosCreator)中的应用,帮助开发者更好地理解和运用向量操作。
本文深入探讨了向量的点乘和叉乘概念,包括计算公式、矩阵表示及实际应用。点乘用于计算向量夹角、投影和判断方向一致性;叉乘涉及判断向量方位、确定点在平面位置。通过实例展示了在游戏开发(如CocosCreator)中的应用,帮助开发者更好地理解和运用向量操作。
















 5074
5074

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








