经典休哈特SPC算法与现代智能SPC算法的比较

作者：Juergen Ude

经典 SPC（统计过程控制）技术是由休哈特100多年前提出，那时没有现代计算能力且生产过程非常简单。受技术限制那个时代的大师们不得不对过程提出很多不合理的假设。最基础的假设是：

“数据服从正态分布，且过程固有的波动仅存在于子组内。”

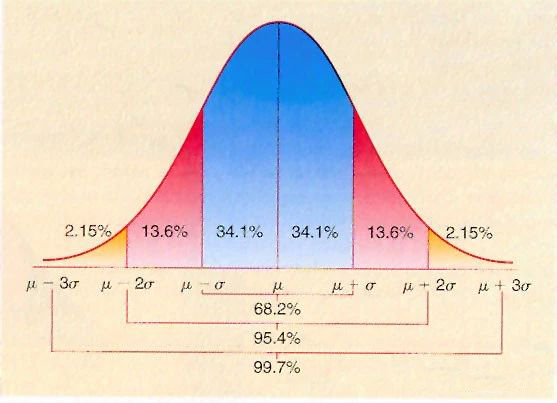
随着时代的发展，SPC早已形成巨大咨询业务市场。但是，大部分咨询顾问似乎只是照本宣科，从不质疑。有趣的是，实干家休哈特却倡导：“布丁好不好吃，只有吃了才知道”，即实践是检验真理的唯一标准。

虽然 SPC 这个术语涵盖的范围不止控制图，但本文仅从“正态假设”谈起，讨论以统计学为基础的控制图。

经典 SPC 与优化算法 SPC 最重要的区别是新技术不假设数据服从正态分布。通过优化算法，新技术能够获得数据的实际分布，并基于此分布绘制控制图进行分析控制。

正态假设

经典SPC理论基础为正态分布。实际环境中非正态分布的场景随处可见，休哈特也意识到了这一点，所以在其理论公式中引入了纠偏参数用来增强经典SPC模型对于非正态数据的稳健性。

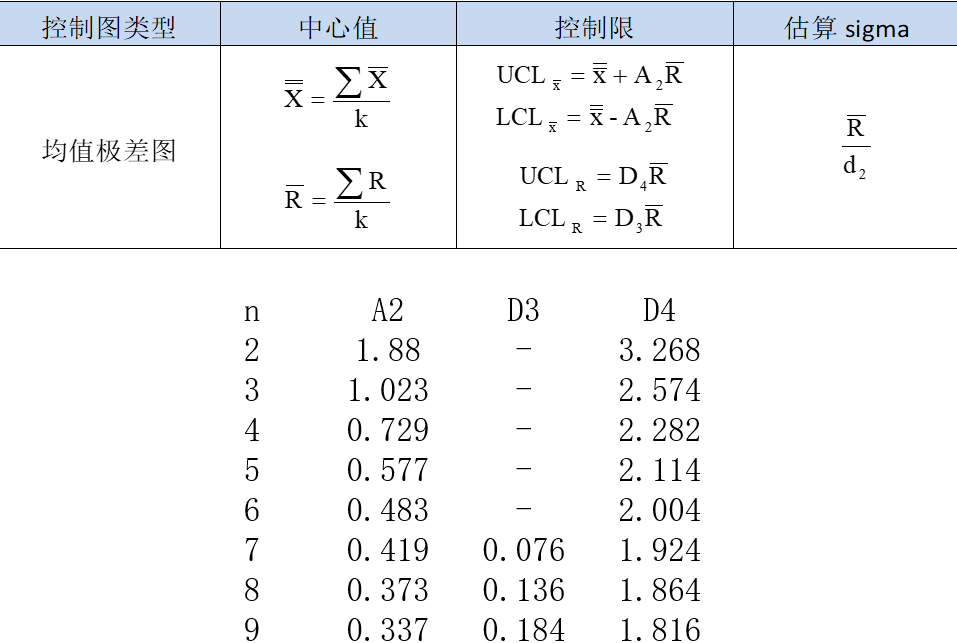
休哈特在其《工业产品质量的经济控制》一书中声称，即使样本量为4，均值的分布也是正态的。因此，休哈特均值图和后来的移动均值图和指数加权移动均值图被普遍接受，即使严重的偏离正态都认为是稳健的。但经典模型对于非正态数据并没有宣传的那样稳健。

接下来将证明均值图对非正态数据稳健的假设并非总是如此。

实践验证

让我们来检验一下。我们通过研究一个受控过程的3种不同分布的非正态性对假警报的影响，来检验均值图对非正态性的敏感性。

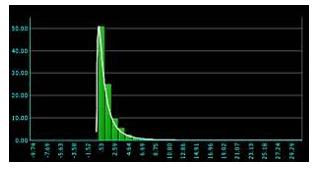
图1：高度偏态分布

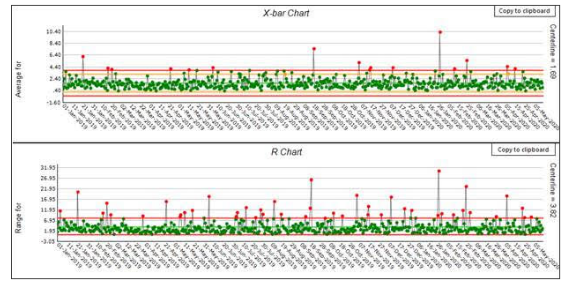
图2：均值极差图（基于图1数据，子组大小为5）

这个例子看似是“精挑细选”的极端情况，用于强调存在问题，但在实践中，这些类型的分布经常遇到。

500个点中，均值图有16个失控点，3次超出警告限。极差图有45个失控点。正如预测的那样，因为极差没有做均值处理，因此极差图表现的更差一些。

仅此一点就表明，均值图对非正态数据并不像休哈特所说的那样稳健。如图3所示，均值处理并没有显著地使数据正态化。

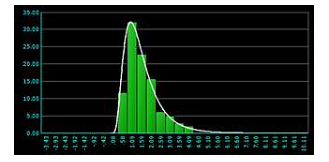
图3：子组均值的分布（基于图1 数据）

图4所示的分布是比图1更温和的非正态分布。

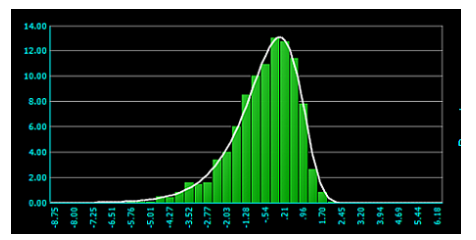
图4：与图1相比，一个更为温和的非正态分布

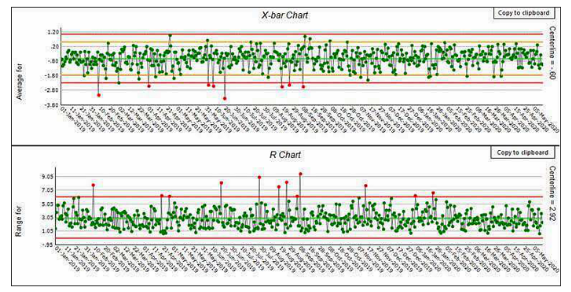
图5：均值极差图（基于图4数据，子组大小为5）

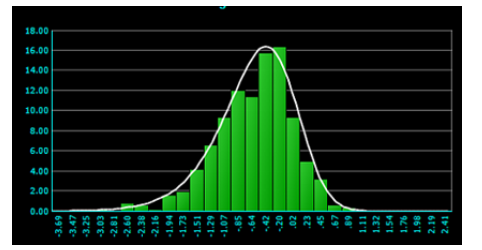
图6：子组均值的分布（基于图4 数据）

图6显示，与图1相比，该分布更正态化。然而，在500个点中，均值图有8个失控点，而极差图有12个。

上述例子表明均值图特别是极差图对非正态性非常不稳健。如中心极限定理所述：当样本量接近无穷大时，所有连续分布接近正态分布。然而，与无穷大相比，实际应用均值图时使用的样本量非常小。

上述事例的所有数据都是从模拟的受控过程中独立获得，这就得出结论，计算出的控制限是不适合的。

即使休哈特明白问题的严重性，在休哈特的时代，也不可能处理非正态的问题。即便现在，也没有像休哈特均值图那样简单的通过手工就能计算控制限的公式。这可能就是为什么控制图技术像尘封在“时间胶囊”中几乎没有改变的原因。

由于现代计算机的发展，现在可以利用Machine Power(计算机的数字运算能力)和智能算法来绘制非正态数据的控制图。基于Machine Power 算法的新技术无需正态假设，可获取数据的实际分布，对非正态数据更稳健，更符合实际情况。

分布优化控制图

经典SPC控制图基于正态分布假设，利用纠偏参数计算控制限。基于Machine Power算法的分布优化控制图，根据数据实际分布计算控制限，对正态分布更稳健。

我们还是遵循休哈特的倡导：“布丁好不好吃，只有吃了才知道”。为了了解这项技术是否有效，使用Machine Power算法分析上述图表的数据。

图7是基于图2控制图数据的分布优化控制图。休哈特控制图有16个超出上限的失控点，而分布优化图只有2个高于上限2个低于上限（紧紧地挨着），考虑到ARL的可变性，对于所选择的0.00135（相当于3σ的常规控制限）的概率点来说，这并不意外。极差图只有1个失控点。相比之下，使用休哈特均值图和极差图有45个失控点。

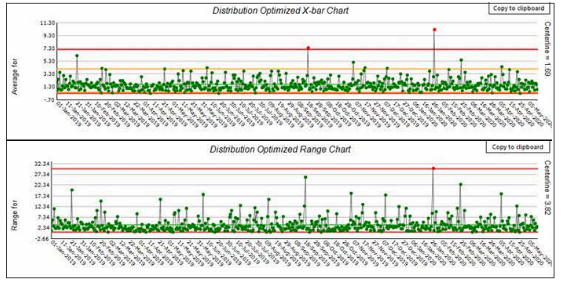
图7：均值极差图（基于图2数据，子组大小为5）

图8是基于图4控制图数据的分布优化控制图。休哈特控制图有8个低于下限的失控点，而分布优化图只有2个高于下限1个低于下限，这对于所选择的0.00135（相当于3σ的常规控制限）的概率点来说也并非意外。极差图只有2个超出失控点。相比之下，使用休哈特均值图和极差图有12个失控点。

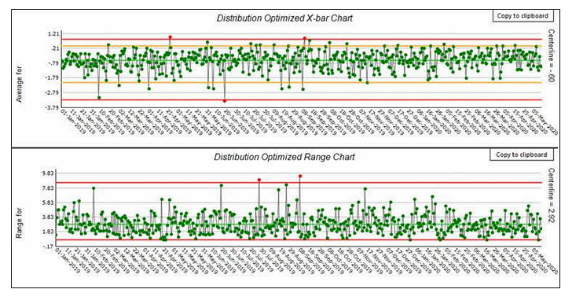
图8：均值极差图（基于图5数据，子组大小为5）

通过上述模拟数据的对比分析，可以发现基于数据实际分布计算的控制限对非正态分布数据更符合实际情况，更具指导意义。对于正态分布数据，两种算法的控制限是一致的。这为现代生产环境下的过程控制提供了新选择。