从e系到g系更形象的理解方式。如图所示:
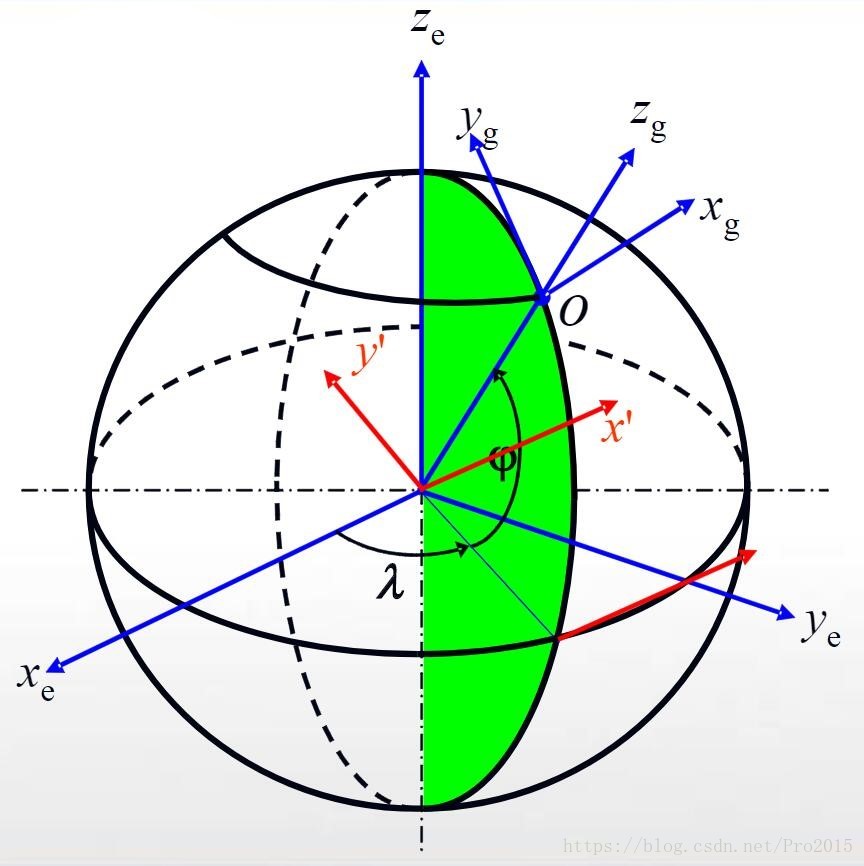
图中,λ\lambdaλ表示经度,φ\varphiφ表示纬度。
当e系绕zez_eze轴正向旋转λ\lambdaλ,那么此时xex_exe轴就在本初子午面上,过本初子午线与赤道线的交点。此时xex_exe轴的指向为的天方向。
观察g系中xgx_gxg轴的指向,其指向东方向。此时xex_exe与xgx_gxg还相差90∘90^\circ90∘,所以还要再旋转90∘90^\circ90∘。即e系绕zez_eze轴正向旋转λ+90∘\lambda+90^\circλ+90∘便能使xex_exe与xgx_gxg同向。
之后便需要绕xex_exe轴旋转,如果让zez_eze与zgz_gzg同向,便实现了两个坐标系的旋转变换。
zgz_gzg与赤道平面的夹角为φ\varphiφ,那么与zez_eze的夹角为90∘−φ90^\circ-\varphi90∘−φ,因此绕xex_exe轴旋转90∘−φ90^\circ-\varphi90∘−φ即可。
这样便实现了从e系到g系的转换。
绕zez_eze轴旋转λ+90\lambda + 90λ+90:
[cos(λ+90∘)sin(λ+90∘)0−sin(λ+90∘)cos(λ+90∘)0001]=[−sinλcosλ0−cosλ−sinλ0001]
\begin{bmatrix}
cos(\lambda+90^\circ) & sin(\lambda+90^\circ) & 0\\
-sin(\lambda+90^\circ) & cos(\lambda+90^\circ) & 0\\
0 & 0 & 1\\
\end{bmatrix} =
\begin{bmatrix}
-sin\lambda & cos\lambda & 0\\
-cos\lambda & -sin\lambda & 0\\
0 & 0 & 1\\
\end{bmatrix}
⎣⎡cos(λ+90∘)−sin(λ+90∘)0sin(λ+90∘)cos(λ+90∘)0001⎦⎤=⎣⎡−sinλ−cosλ0cosλ−sinλ0001⎦⎤
绕xex_exe轴旋转90−φ90-\varphi90−φ:
[1000cos(90∘−φ)sin(90∘−φ)0−sin(90∘−φ)cos(90∘−φ)]=[1000sinφcosφ0−cosφsinφ]
\begin{bmatrix}
1 & 0 & 0\\
0 & cos(90^\circ - \varphi) & sin(90^\circ - \varphi)\\
0 & -sin(90^\circ - \varphi) & cos(90^\circ - \varphi)\\
\end{bmatrix} =
\begin{bmatrix}
1 & 0 & 0\\
0 & sin\varphi & cos\varphi\\
0 & -cos\varphi & sin\varphi
\end{bmatrix}
⎣⎡1000cos(90∘−φ)−sin(90∘−φ)0sin(90∘−φ)cos(90∘−φ)⎦⎤=⎣⎡1000sinφ−cosφ0cosφsinφ⎦⎤
可得:
Ceg=[1000sinφcosφ0−cosφsinφ][−sinλcosλ0−cosλ−sinλ0001]=[−sinλcosλ0−sinφcosλ−sinφsinλcosφcosφcosλcosφsinλsinφ]
C_e^g =
\begin{bmatrix}
1 & 0 & 0\\
0 & sin\varphi & cos\varphi\\
0 & -cos\varphi & sin\varphi
\end{bmatrix}
\begin{bmatrix}
-sin\lambda & cos\lambda & 0\\
-cos\lambda & -sin\lambda & 0\\
0 & 0 & 1\\
\end{bmatrix} =
\begin{bmatrix}
-sin\lambda & cos\lambda & 0 \\
-sin\varphi cos\lambda & -sin\varphi sin\lambda & cos\varphi \\
cos\varphi cos\lambda & cos\varphi sin\lambda & sin\varphi
\end{bmatrix}
Ceg=⎣⎡1000sinφ−cosφ0cosφsinφ⎦⎤⎣⎡−sinλ−cosλ0cosλ−sinλ0001⎦⎤=⎣⎡−sinλ−sinφcosλcosφcosλcosλ−sinφsinλcosφsinλ0cosφsinφ⎦⎤
Cge=[−sinλ−sinφcosλcosφcosλcosλ−sinφsinλcosφsinλ0cosφsinφ]
C_g^e =
\begin{bmatrix}
-sin\lambda & -sin\varphi cos\lambda & cos\varphi cos\lambda\\
cos\lambda & -sin\varphi sin\lambda & cos\varphi sin\lambda\\
0 & cos\varphi & sin\varphi
\end{bmatrix}
Cge=⎣⎡−sinλcosλ0−sinφcosλ−sinφsinλcosφcosφcosλcosφsinλsinφ⎦⎤





















 3142
3142

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








