如需要数据及源码,关注微信公众号【爱敲代码的破晓】,后台私信【20260109】
一、KNN时间序列预测原理
1. 基本思想
KNN(K最近邻)时间序列预测的核心思想是"历史会重演"。算法假设相似的过去模式会导致相似的未来结果。通过寻找当前序列模式在历史数据中最相似的K个邻居,用这些邻居的未来值来预测当前序列的未来值。
2. 监督学习转换
将时间序列预测问题转换为监督学习问题。通过滑动窗口技术,将连续的时间序列数据转换为特征-标签对:
-
特征:过去N个时间点的序列值
-
标签:下一个时间点的序列值
这样就把时间依赖性转化为特征空间中的空间相似性。
3. 相似性度量
使用距离度量(如欧氏距离、曼哈顿距离)来量化序列模式之间的相似性。当前时间窗口与历史时间窗口的距离越小,说明两个序列模式越相似。
4. 预测机制
对于当前的时间窗口:
-
计算它与所有历史时间窗口的距离
-
选择距离最小的K个邻居
-
基于这K个邻居的下一个时间点的值进行预测
-
预测方式可以是平均值(uniform)或距离加权平均(distance-weighted)
5. 参数选择关键
-
K值:平衡偏差和方差的关键参数,小K值对噪声敏感,大K值可能平滑掉重要模式
-
时间窗口大小:决定了考虑多少历史信息,需要根据序列的周期性和自相关性确定
-
距离度量:影响相似性判断的标准,欧氏距离常用但可能对尺度敏感
6. 无模型假设
KNN是惰性学习算法,不对数据分布做任何假设。这种非参数特性使其能够适应各种复杂的时间序列模式,包括非线性、非平稳的模式。
7. 局部模式捕捉
特别擅长捕捉时间序列中的局部模式重复,对于具有循环模式、季节性模式的时间序列效果较好。算法只关注最相似的局部模式,而不是全局模式。
二、KNN与其他时间序列预测算法的优势比较
1. 相对于传统统计方法(ARIMA、ETS等)
-
无需模型假设:ARIMA需要数据平稳、残差独立等严格假设,KNN无需任何统计假设
-
非线性处理:能自动捕捉非线性关系,而传统方法主要处理线性关系
-
灵活性:适应各种复杂模式,不需要手动识别季节周期、趋势类型
-
多模态处理:能处理具有多个不同模式的时间序列
2. 相对于深度学习(LSTM、GRU等)
-
训练速度快:KNN没有训练过程,只有存储和搜索,特别适合小到中等数据集
-
可解释性强:预测基于具体的邻居实例,可以追溯到相似的历史模式
-
超参数少:主要需要调优K值和窗口大小,调参相对简单
-
小样本友好:在小数据集上表现稳定,不容易过拟合
-
无梯度问题:不存在梯度消失或爆炸问题
3. 相对于树模型(随机森林、XGBoost等)
-
计算效率:对于实时预测,KNN的预测速度通常更快
-
参数敏感性低:相对更少的超参数需要调优
-
边界处理:在特征空间边界处的预测通常更稳定
-
距离直观:基于距离的相似性判断比树的分裂规则更直观
4. 相对于Prophet等专门的时间序列方法
-
通用性:不限于特定类型的时间序列模式
-
无先验知识要求:不需要指定季节周期、节假日等先验信息
-
适应性:能快速适应序列模式的变化
-
实现简单:算法简单,容易实现和调试
5. 相对于简单基准方法(滑动平均、指数平滑等)
-
模式识别能力:不仅能平滑序列,还能识别和利用特定模式
-
动态适应性:根据当前模式动态选择参考的历史数据
-
多尺度信息:通过调整K值和窗口大小,可以捕捉不同时间尺度的模式
6. 独特优势总结
-
概念简单直观:基于"相似历史导致相似未来"的直观思想
-
零训练时间:训练阶段只是存储数据,特别适合在线学习场景
-
增量学习友好:新数据可以无缝加入,不需要重新训练整个模型
-
多步预测稳定:递归多步预测时相对稳定,误差累积较小
-
缺失数据鲁棒:对缺失值和异常值有一定的鲁棒性
-
多变量扩展易:容易扩展到多变量时间序列,只需扩展特征维度
7. 应用场景优势
-
周期性明显的时间序列:对于具有明显重复模式的序列效果显著
-
小到中等规模数据:在数据量不大时通常能取得不错效果
-
快速原型开发:快速验证时间序列预测问题的可行性
-
实时预测系统:适合需要快速响应的实时预测场景
-
模式变化快的序列:能快速适应序列模式的突然变化
8. 作为基准模型的优势
-
建立合理基准:KNN通常能提供比简单平均更好的基准表现
-
特征工程验证:可以用来验证时间序列特征工程的有效性
-
模型复杂度参考:帮助确定是否需要更复杂的模型
KNN时间序列预测虽然简单,但在许多实际应用中表现出色,特别适合作为第一尝试的算法或基准模型。它的主要局限性在于对大规模数据和高维特征的处理效率,以及对长期依赖关系的捕捉能力有限。
三、KNN在时间序列预测中是应用示例
1. 数据准备
2.导入第三方库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import joblib
import os
import warnings
warnings.filterwarnings('ignore')
3.脚本参数配置
# 数据参数
DATA_PATH = '20260109.csv' # CSV文件路径
TARGET_COLUMN = 'Open' # 目标列
DATE_COLUMN = 'Date' # 日期列
TEST_SIZE = 0.2 # 测试集比例
RANDOM_STATE = 42 # 随机种子
# KNN模型参数
LOOK_BACK = 10 # 时间窗口大小
K_NEIGHBORS = 5 # KNN的K值
WEIGHTS = 'uniform' # 'uniform' 或 'distance'
ALGORITHM = 'auto' # 'auto', 'ball_tree', 'kd_tree', 'brute'
# 图形参数
PLOT_SIZE = (12, 8)
DPI = 100
SAVE_FIGURES = True
OUTPUT_DIR = 'outputs/'
4.读取数据并预处理
# 1. 读取数据
print("1. 读取数据...")
df = pd.read_csv(DATA_PATH)
df[DATE_COLUMN] = pd.to_datetime(df[DATE_COLUMN])
df.set_index(DATE_COLUMN, inplace=True)
# 只使用Open列
data = df[TARGET_COLUMN].values.reshape(-1, 1)
dates = df.index
print(f"数据形状: {data.shape}")
print(f"数据时间范围: {dates.min()} 到 {dates.max()}")
# 2. 数据标准化
print("\n2. 数据标准化...")
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
5.划分训练集和测试集
# 4. 划分训练集和测试集
print("\n4. 划分数据集...")
train_size = int(len(X) * (1 - TEST_SIZE))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
dates_train, dates_test = dates_X[:train_size], dates_X[train_size:]
print(f"训练集大小: {len(X_train)}")
print(f"测试集大小: {len(X_test)}")
6.训练模型
# 5. 训练KNN模型
print("\n5. 训练KNN模型...")
print(f"K值: {K_NEIGHBORS}")
print(f"权重: {WEIGHTS}")
knn_model = KNeighborsRegressor(
n_neighbors=K_NEIGHBORS,
weights=WEIGHTS,
algorithm=ALGORITHM
)
knn_model.fit(X_train, y_train)
7.模型预测
# 6. 预测
print("\n6. 进行预测...")
y_train_pred = knn_model.predict(X_train)
y_test_pred = knn_model.predict(X_test)
# 反标准化
y_train_actual = scaler.inverse_transform(y_train.reshape(-1, 1)).flatten()
y_test_actual = scaler.inverse_transform(y_test.reshape(-1, 1)).flatten()
y_train_pred_actual = scaler.inverse_transform(y_train_pred.reshape(-1, 1)).flatten()
y_test_pred_actual = scaler.inverse_transform(y_test_pred.reshape(-1, 1)).flatten()
8.模型评估并绘图
# 7. 计算评估指标
print("\n7. 计算评估指标...")
metrics = {}
for name, y_true, y_pred in [
("训练集", y_train_actual, y_train_pred_actual),
("测试集", y_test_actual, y_test_pred_actual)
]:
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_true, y_pred)
mape = np.mean(np.abs((y_true - y_pred) / y_true)) * 100
r2 = r2_score(y_true, y_pred)
metrics[name] = {
'MSE': mse,
'RMSE': rmse,
'MAE': mae,
'MAPE': mape,
'R2': r2
}
print(f"\n{name}评估指标:")
print(f" MSE: {mse:.4f}")
print(f" RMSE: {rmse:.4f}")
print(f" MAE: {mae:.4f}")
print(f" MAPE: {mape:.2f}%")
print(f" R²: {r2:.4f}")
9.保存模型
# 8. 保存模型和结果
print("\n8. 保存模型和结果...")
# 保存模型
model_info = {
'model': knn_model,
'scaler': scaler,
'look_back': LOOK_BACK,
'train_size': train_size,
'metrics': metrics,
'dates_train': dates_train,
'dates_test': dates_test,
'y_train_actual': y_train_actual,
'y_test_actual': y_test_actual,
'y_train_pred': y_train_pred_actual,
'y_test_pred': y_test_pred_actual,
'train_params': {
'k_neighbors': K_NEIGHBORS,
'weights': WEIGHTS,
'algorithm': ALGORITHM
}
}
joblib.dump(model_info, os.path.join(OUTPUT_DIR, 'knn_model.pkl'))
print(f"模型已保存到: {os.path.join(OUTPUT_DIR, 'knn_model.pkl')}")
# 保存评估指标
metrics_df = pd.DataFrame({
'数据集': ['训练集', '测试集'],
'MSE': [metrics['训练集']['MSE'], metrics['测试集']['MSE']],
'RMSE': [metrics['训练集']['RMSE'], metrics['测试集']['RMSE']],
'MAE': [metrics['训练集']['MAE'], metrics['测试集']['MAE']],
'MAPE': [metrics['训练集']['MAPE'], metrics['测试集']['MAPE']],
'R2': [metrics['训练集']['R2'], metrics['测试集']['R2']]
})
metrics_df.to_csv(os.path.join(OUTPUT_DIR, 'evaluation_metrics.csv'), index=False)
print(f"评估指标已保存到: {os.path.join(OUTPUT_DIR, 'evaluation_metrics.csv')}")
# 9. 绘制训练过程图
print("\n9. 绘制训练结果图...")
plot_training_results(model_info)
print("\n" + "=" * 60)
print("训练完成!")
print("=" * 60)
以下是结果
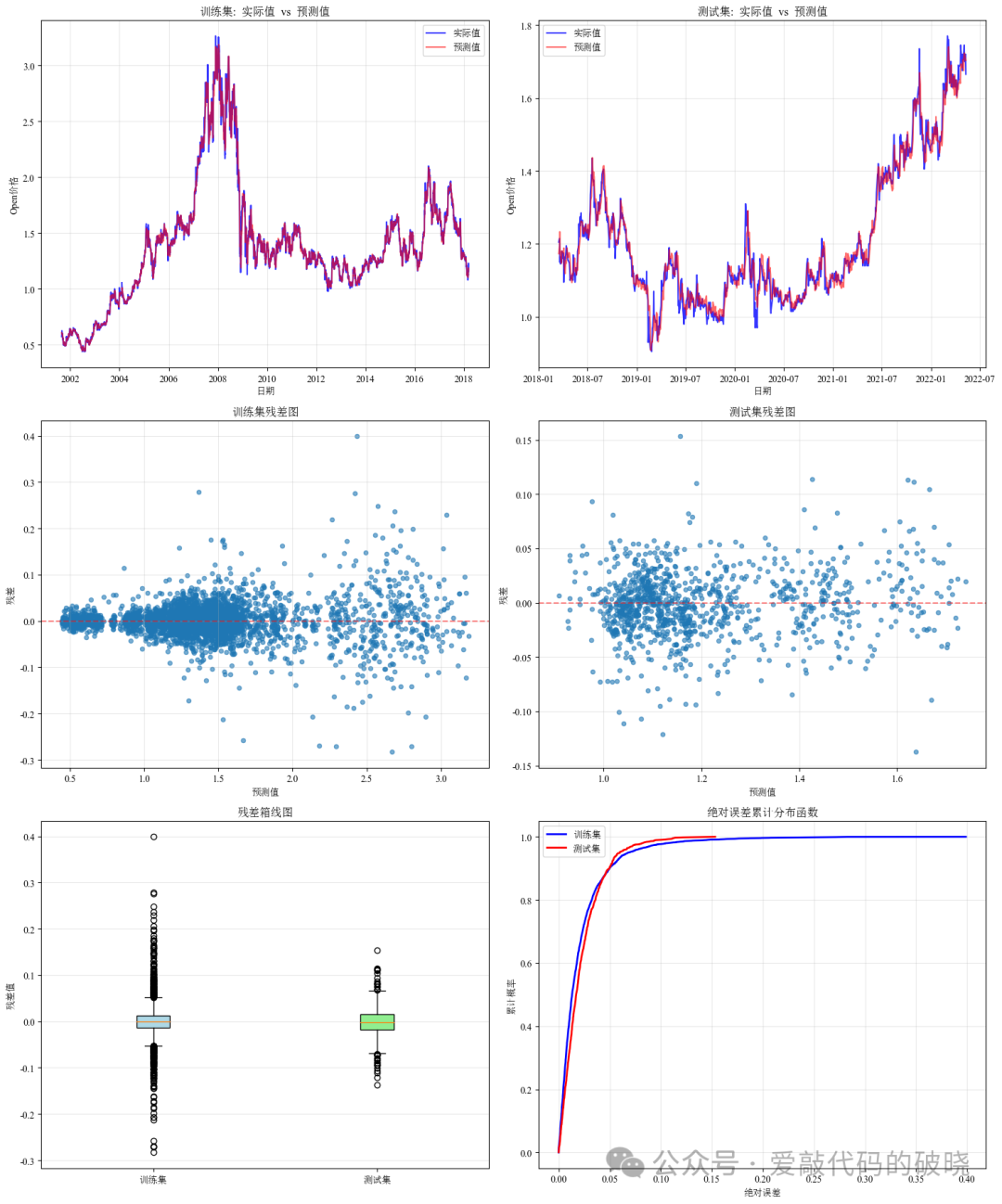
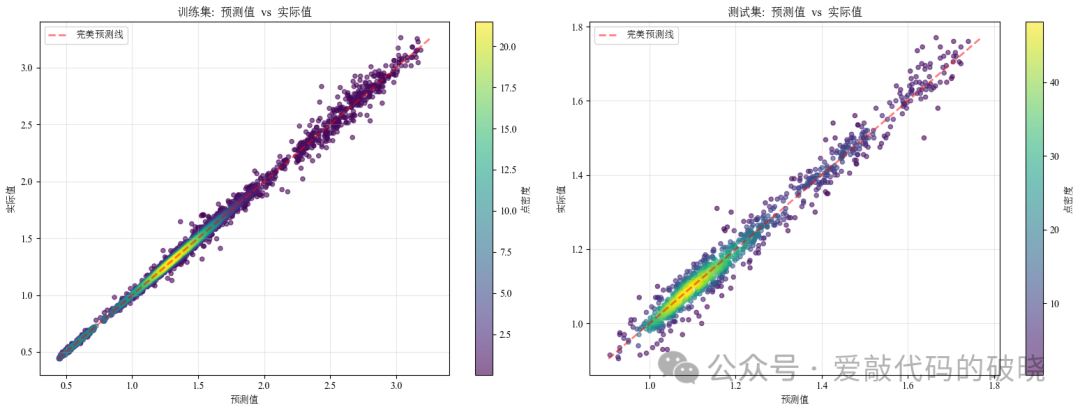
同时,MSE、RMSE、MAE、MAPE、R²这4个参数对结果进行评估,控制台输出结果如下:






















 380
380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








