硅基计划4.0 算法 二分查找

文章目录
一、二分查找
题目链接
这道题就是最简单的二分查找题,在正式解题之前,我想先来讲讲二分查找算法
可能大家之前已经了解过了这个算法,我之前文章也有介绍过,但是我想说,二分查找不止于此
我们接下来先讲讲最普通的二分查找算法
二分查找,本质上是二段性,不一定要以1/2作为分割点,1/3,1/4等等也可以
但是为什么推荐用1/2作为分割点呢,因为这样子时间复杂度是最小的,证明可以去网上搜搜
好,我们二分查找的核心是不是设立两个指针,一个在最左边一个在最右边,然后相互靠拢,当两个指针位置互换了循环就结束了
好,那我的循环条件是写成left<=right还是写成left<right呢?
我们推荐写成left<=right,为什么?
你想,我们每一次二分查找,区间都是未知的,到最后的时候,即使区间收缩成一个点,这个点我们还是未知的,我们还是要进行判断的
好,那我们如何去寻找中间元素呢?
我们为了避免超出数据范围即溢出的风险,我们采用left+(right-left)/2,即左指针加上整体长度的一半
当然,我们求中间元素还有left+(right-left+1)/2
这两个有什么区别呢,我们看到它们区别就是+1的问题
在奇数个元素下,求的中间节点都是一样的,而在偶数个元素下
上面那个求中间元素,求的中间元素是在中间的第一个元素,即[0,1,2,3]中间元素是1
下面那个求中间元素,求的中间元素是在中间的第二个元素,即[0,1,2,3]中间元素是2
好,我们最后来分析时间复杂度,求一次二分,排查剩下
n
2
\frac{n}{2}
2n个元素
求第二次二分,排查剩下
n
4
\frac{n}{4}
4n个元素…求第x次二分,排查剩下
1
2
x
\frac{1}{2^x}
2x1
因此等差数列求和后是
2
x
=
n
2^x=n
2x=n,化简成
x
=
l
o
g
n
x=logn
x=logn
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left <= right){
int middle = left+(right-left)/2;
if(nums[middle] > target){
right = middle-1;
}else if(nums[middle] < target){
left = middle+1;
}else{
return middle;
}
}
return -1;
}
}
二、排序数组中查找指定元素第一个位置和最后一个位置
题目链接
这道题我们看到是一个有序的数组,那我们就可以利用单调性使用二分查找了
1. 先找左端点
我们把原数组划分成两个区域,一个区域是<target,一个区域是>target
- 当中间元素值比
target小的时候,不可能是我们的最终结果,此时我们的左指针要去中间元素右边寻找,即left = middle +1 - 当中间元素值
>=target时候,可能是我们的最终结果,即我们要找的左端点,也可能不是,因此我们的right = middle
为什么我们的
right不能去middle左边呢?因为middle可能正好是我们要找的左端点
好,我们来讨论细节问题
- 为什么循环终止条件是
left < right呢?
你想,我们最后如果能找到结果,此时一定left = right,那我们都把周边区域排查完了,此时我们就没必要排查了,这一点和普通二分查找不一样
还有最重要的是,当我们的原始数组内所有的值都比target目标值大,此时right就会一直不断向左移,直到和left相遇,此时就是我们的最后结果
当我们的原始数组值都比target小,left就会向右移,直到和right相遇
上述两种情况,当它们相遇的时候,由于循环是left <= right,它们会一直原地判断,导致死循环 - 为什么求中点使用
left+(right-left)/2而不使用left+(right-left+1)/2呢?
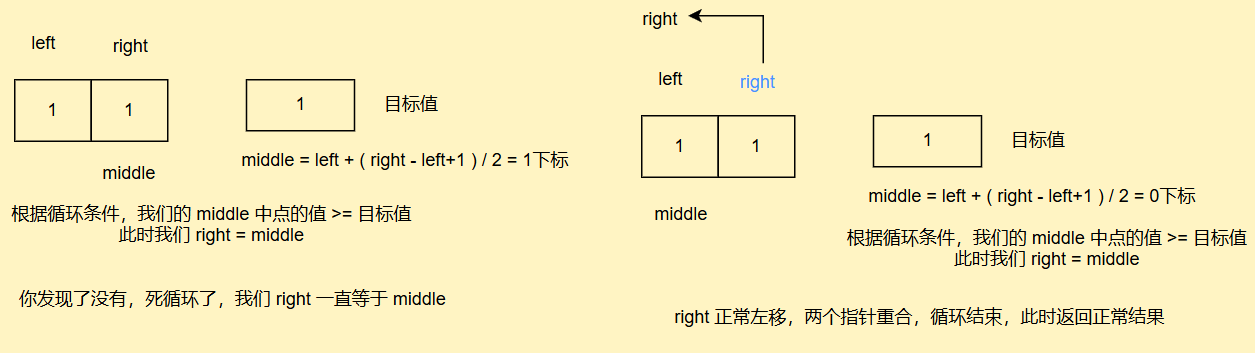
2. 再找右端点
跟刚刚找左端点一样,是反着来的
- 当中间元素值
>target的时候,不可能是我们的最终结果,此时我们的右指针要去中间元素左边寻找,即right = middle -1 - 当中间元素值
<=target时候,可能是我们的最终结果,即我们要找的右端点,也可能不是,因此我们的left = middle
为什么我们的
left不能去middle右边呢?因为middle可能正好是我们要找的右端点
好,我们继续来讨论细节问题
- 为什么循环终止条件还是
left < right呢?
原因和刚刚一样的,相等的时候就是最终结果,无需判断,也避免死循环 - 为什么求中点使用
left+(right-left+1)/2而不使用left+(right-left)/2呢?
这里就和刚刚不一样了,我们还是用画图来演示一下

3. 编写代码
class Solution {
public int[] searchRange(int[] nums, int target) {
int [] ret = {-1,-1};
int length = nums.length;
if(length == 0){
return ret;
}
if(target > nums[length-1]){
return ret;
}
int left = 0;
int right = length-1;
//找左端点
while(left < right){
int middle = left+(right-left)/2;
if(nums[middle] < target){
left = middle+1;
}else{
right = middle;
}
}
//判断左端点是否找到了结果
if(nums[left] == target){
ret[0] = left;
}else{
return ret;
}
//找右端点
right = length-1;
while(left < right){
int middle = left+(right-left+1)/2;
if(nums[middle] > target){
right = middle-1;
}else{
left = middle;
}
}
ret[1] = right;
return ret;
}
}
三、x平方根
题目链接
这一题和上一题类似,我们把数组划分成两个区域
middle*middle <= 目标值,left = middlemiddle*middle > 目标值,right = middle-1
class Solution {
public int mySqrt(int x) {
if(x < 1){
return x;
}
long left = 0;
long right = x;
while(left < right){
long middle = left+(right-left+1)/2;
if(middle*middle > x){
right = middle-1;
}else{
left = middle;
}
}
return (int)left;
}
}
四、搜索插入位置
题目链接
这道题唯一需要注意的是如果数组末尾的数(最大数)比目标值还要小的话,说明我们插入的数要插入到数组末尾,即left+1位置(此时left会走到最后一个位置)
否则我们就正常放入left循环结束后的位置就好
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left <= right){
int middle = left+(right-left)/2;
if(nums[middle] > target){
right = middle-1;
}else if(nums[middle] < target){
left = middle+1;
}else{
return middle;
}
}
//此时说明不存在数组中,看最后一个值是否大于目标值
return nums[nums.length-1] > target ? right+1 : left;
}
}
五、山脉数组峰顶索引
题目链接
根据单调性去解决问题就好,直接二分查找就行,不过多赘述
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left = 0;
int right = arr.length-1;
while(left < right){
int middle = left+(right-left)/2;
if(arr[middle] >= arr[middle+1]){
right = middle;
}else{
left = middle+1;
}
}
return left;
}
}
六、寻找峰值
题目链接
这题因为只需要返回一个峰值就好,和上一题一模一样的代码
class Solution {
public int findPeakElement(int[] nums) {
int left = 0;
int right = nums.length-1;
while(left < right){
int middle = left+(right-left)/2;
if(nums[middle] >= nums[middle+1]){
right = middle;
}else{
left = middle+1;
}
}
return left;
}
}
七、寻找旋转排序数组最大值
题目链接
这题数组特点就是从头到尾先增大,后迅速减小,又增大,像两个坡
但是你观察到,因为旋转之前是有序的数组,因此我们可以很明确的直到,数组最左边的值一定是大于数组最右边的值的,不信您可以看看示例
我们可以利用这个特性,以数组末尾的数作为参照,我们分为两种情况
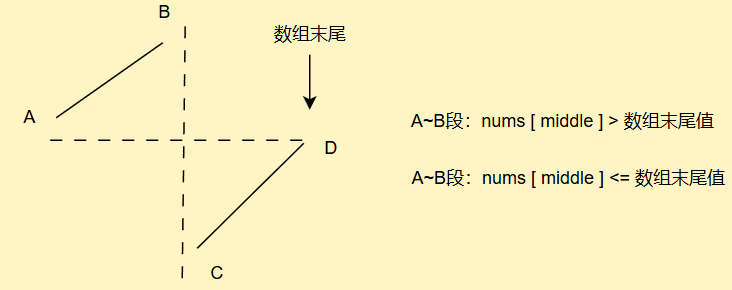
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length-1;
// 先处理数组未旋转的情况
if(nums[left] <= nums[right]) {
return nums[left];
}
while(left < right) {
int mid = left + (right-left)/2;
// 与第一个元素比较
if(nums[mid] >= nums[0]) {
// 中间值在左半部分(较大段)
left = mid+1;
} else {
// 中间值在右半部分(较小段)
right = mid;
}
}
return nums[left];
}
}
你说,我们以数组起始位置为参考点可以吗,可以,但是有一种特殊情况
就是如果数组是完全有序的,那我们最后left会变到middle+1位置,并不是起始位置了
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length-1;
// 先处理数组未旋转的情况
if(nums[left] <= nums[right]) {
return nums[left];
}
while(left < right) {
int mid = left + (right-left)/2;
// 与第一个元素比较
if(nums[mid] >= nums[0]) {
// 中间值在左半部分(较大段)
left = mid+1;
} else {
// 中间值在右半部分(较小段)
right = mid;
}
}
return nums[left];
}
}
八、0~n-1的缺失数字
题目链接
这一题就是说数组值和下标值相同,如果出现错位,请你找出那个缺失的值
这一我们可以用好多种方法,我们先用二分查找方法
有个细节要注意,如果是[0,1,2,3]这种情况,看起来有序,其实它缺失的是数字4,但是4超出了数组范围,因此我们要返回left+1
1. 二分查找
class Solution {
public int takeAttendance(int[] records) {
int left = 0;
int right = records.length-1;
while(left < right){
int middle = left+(right-left)/2;
//根据下标确定
if(records[middle] - middle == 0){
left = middle+1;
}else{
right = middle;
}
}
//left+1针对是是完全有序的数组,最后left会落在数组末尾
//但是缺失的数是末尾数值+1,因此返回left+1,否则正常返回left
return left == records[left] ? left+1 : left;
}
}
2. 模拟哈希表
class Solution {
public int takeAttendance(int[] records) {
boolean[] exists = new boolean[records.length + 1];
for (int num : records) {
if (num < exists.length) {
exists[num] = true;
}
}
for (int i = 0; i < exists.length; i++) {
if (!exists[i]) {
return i;
}
}
return -1; // 不会执行
}
}
3. 位运算
class Solution {
public int takeAttendance(int[] records) {
int result = records.length; // 初始化结果为n
for (int i = 0; i < records.length; i++) {
result ^= i;
result ^= records[i];
}
return result;
}
}
4. 高斯求和
class Solution {
public int takeAttendance(int[] records) {
int n = records.length;
long total = (long) n * (n + 1) / 2; // 0到n的总和
long sum = 0;
for (int num : records) {
sum += num;
}
return (int) (total - sum);
}
}
5. 直接遍历
class Solution {
public int takeAttendance(int[] records) {
int n = records.length;
for (int i = 0; i < n; i++) {
if (records[i] != i) {
return i;
}
}
return n; // 缺失的是最后一个数
}
}
6.综合分析
| 方法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 直接遍历 | O(n) | O(1) |
| 高斯求和 | O(n) | O(1) |
| 位运算 | O(n) | O(1) |
| 模拟哈希表 | O(n) | O(1) |
| 二分查找 | O(log n) | O(1) |
因此对于本题数组的有序性,使用二分查找是最优解




















 1863
1863

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








