硅基计划4.0 算法 前缀和

一、一维前缀和
题目链接
这道题就是我们一维前缀和的模板,接下来我会详细讲解原理
我们先来理解题意
题目中说数组从1下标开始,也就是说0下标的元素是默认值,为什么要这么干,稍后解释
输入示例中
第一行第一个数字3代表有三个元素
第二个数字2达标要进行2次查询
第二行是给的输入数组
第三行中1和2指的是从下标1到下标2区间内的元素之和,求和结果是3
第四行中2和3是指是从下标2到下标3区间内的元素之和,求和结果是6
倘若给出2 2,指的就是求下标2一个元素就好
好,题目解析完毕,我们来讲讲算法原理
既然要求的是区间的和,那我们就可以遍历数组,根据你要查询的区间,求出对应区间的和就好
但是,这样时间复杂度就很高,为什么高呢,你想,如果每次查询都从头开始,是不是总共要查询O(n*q)这么多
因此,我们利用数组是正数的原理,可以这样
我们可以先预处理一个前缀和数组dp[],其中dp[i]代表的是从[1,i]位置的元素之和
这就是我们动态规划里的状态表示
好,我们怎么求出dp[]中的每一个元素呢,其实很简单,你想想,我们求的是区间的和
那我们要求当前区间的和,是不是只需要先把从头到当前位置的和先算出来,然后减去前面区间的和,就是当前区间的和啦
比如[1,2,3,4],我们要求最后两个数字的区间的和,是不是只需要把整个数组和算出来,然后减去[1,2]就好
因此我们可以得到递推公式,即状态转移方程dp[i] = dp[i-1]+arr[i]
那我们有了dp[]数组,是不是就可以去使用了,如何使用
我们很容易得出区间公式[i,j] = dp[i] - dp[j-1],为什么要减一呢,因为我们求的是[1,j]区间,包括了j自己

好,我们现在来回答为什么数组下标要从1开始,倘若我求的是原数组[0,2]区间的和,根据公式,那我应该是dp[2] - dp [-1],而-1会导致越界
因此我们dp[0]保持默认值,充当边界作用,而且我们保持默认值0,并不会影响最终结果
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
int n = in.nextInt(),m = in.nextInt();
int [] arr = new int[n+1];
for(int i = 1;i<arr.length;i++){
arr[i] = in.nextInt();
}
//预处理前缀和数组,数字可能很大,要用到long
long [] dp = new long[n+1];
for(int i = 1;i<dp.length;i++){
dp[i] = dp[i-1]+arr[i];
}
while(m > 0){
int l = in.nextInt(),r = in.nextInt();
System.out.println(dp[r]-dp[l-1]);
m--;
}
}
}
二、二维前缀和
题目链接
这题比一位前缀和复杂的多,我们先来解读输入示例
第一行数字3和4代表是一个三行四列的矩阵,后面的3代表要进行3次查询
第二、三、四行代表矩阵数字
第五行代表从[1,1]位置到[2,2]位置所围成的区域和,为8
第五行代表从[1,1]位置到[3,3]位置所围成的区域和,为25
第五行代表从[1,2]位置到[3,4]位置所围成的区域和,为32
接下来我们讲解算法原理
暴力解法就不说了,遍历子数组区间就好,时间复杂度O(nmq)
我们利用前缀和思想,预处理一个与原数组同等规模的前缀和的二位数组(矩阵)

好,我们如何使用呢,且看图解

我们来分析下我们的时间复杂度,首先要创建前缀和数组,是O(m,n),再查询O(q),总共就是O(m,n)+O(q)
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
int n = in.nextInt(),m = in.nextInt(),q = in.nextInt();//n行m列q次查询
int [] [] arr = new int[n+1][m+1];
for(int i = 1;i <= n;i++){
for(int j = 1;j<= m;j++){
arr[i][j] = in.nextInt();
}
}
//初始化前缀和数组
long [] [] dp = new long[n+1][m+1];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+arr[i][j];
}
}
while(q > 0){
int x1 = in.nextInt(),y1 = in.nextInt(),x2 = in.nextInt(),y2 = in.nextInt();
System.out.println(dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]);
q--;
}
}
}
三、矩阵区域求和
题目链接
这道题意思是以一个坐标为中心,向周围扩展K个单位,求这个区域内的和

好,我们要怎么求呢,根据我们刚刚讲的二维前缀和的知识就可以求,一模一样,也是求当前区域的和,但是有几个注意的地方
左上角坐标怎么表示,可以这样i-k,右下角同样i+k
就是关于越界的问题,就像刚刚图示一样,因此我们在求边角位置的时候,要让坐标不越界
//左上角位置
(max(0,i-k),max(0,j-k))
//右下角位置,m代表行,n代表列
(min(m-1,i+k),max(n-1,i+k))
还有,力扣中原数组下标从0开始的,当我们寻找(x,y)位置的值的时候,要去原数组中(x-1,y-1)中寻找
因此我们前缀和递推公式要改成dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];
因此我们左上角和右小角位置修改下
//左上角位置
(max(0,i-k)+1,max(0,j-k)+1)
//右下角位置,m代表行,n代表列
(min(m-1mi+k)+1,max(n-1,i+k)+1)
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int row = mat.length;
int column = mat[0].length;
int [] [] dp = new int[row+1][column+1];
for(int i = 1;i < row+1;i++){
for(int j = 1;j < column+1;j++){
dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];
}
}
for(int i = 0;i < row;i++){
for(int j = 0;j < column;j++){
int x2 = Math.min(row-1,i+k)+1;
int y2 = Math.min(column-1,j+k)+1;
int x1 = Math.max(0,i-k)+1;
int y1 = Math.max(0,j-k)+1;
mat[i][j] = dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
}
}
return mat;
}
}
四、寻找数组中心下标
题目链接
这题可以利用我们的前缀和思想,既然是要找到左右两边值相等的下标,那我们不妨这样
我们创造两个数组,一个是前缀f和,一个是后缀和g
但是由于题目是的是不包括当前下标的值得两边要相等
因此f[i]表示[0,i-1]区间内的和,同样g[i]表示[i+1,n-1]区域内的和
因此我们可以得出递推公式f[i] = f[i-1]+nums[i-1] g[i] = g[i+1]+nums[i+1];
最后我们再判断在什么位置相等就好
但是同样还是存在越界问题,你看,当我们求f(1)的时候根据公式f(1) = f(0)+nums(0)
而f(0) = f(-1)+nums(-1),并不存在-1下标
因此我们要初始化f(0) = 0
同样求g(n-2) = g(n-1)+nums(n-1),而g(n-1) = g(n)+nums(n),不存在超过数组长度的下标,因此我们要初始化g(n-1) = 0
因此我们创建前缀和是从左到右,后缀和是从右到左
对于本题,创建数组默认值就是0,因此不需要管了
class Solution{
public int pivotIndex(int[] nums){
int n = nums.length;
int[] lsum = new int[n];//前缀和
int[] rsum = new int[n];//后缀和
// 预处理前缀和后缀和数组
for(int i = 1; i < n; i++){
lsum[i] = lsum[i - 1] + nums[i - 1];
}
for(int i = n - 2; i >= 0; i--){
rsum[i] = rsum[i + 1] + nums[i + 1];
}
// 判断
for(int i = 0; i < n; i++){
if(lsum[i] == rsum[i]){
return i;
}
}
return -1;
}
}
这是只使用一个前缀和数组代码,注意错位问题
class Solution {
public int pivotIndex(int[] nums) {
//注意本题原数组和dp数组位置错开了一位,返回的时候尤其注意
int length = nums.length;//3,对于下标2
int [] dp = new int[length+1];//4,对于下标3
for(int i = 1;i<=length;i++){
dp[i] = dp[i-1]+nums[i-1];
}
for(int i = 1;i<=length;i++){
int leftSum = dp[i-1];
int rightSum = dp[length]-leftSum-nums[i-1];
if(leftSum == rightSum){
return i-1;
}
}
return -1;
}
}
五、除自身以外数组乘积
题目链接
这道题跟刚刚那道题差不多,只是把条件改成算出除当前下标以外的值的乘积
说白了还是可以像刚刚那样去划分区域,我们利用上一题做法,算出前缀积和后缀积再相乘即可
同样我们定义前缀积f和后缀积g
其中f(i)代表就是从[0,i-1]区间内的乘积,g(i)代表就是从[i+1,n-1]区间内的乘积
因此递推公式f(i) = f(i-1)*arr(i-1) g(i) = g(i+1)*arr(i+1)
我们的填表顺序还是f(i)从前往后填,g(i)从后往左填
因此我们的结果数组中ret[i] = f[i]*g[i]
同样我们记得要初始化边界条件,当f(0)时,我们不可以初始化成0,会导致计算结果错误,我们要初始化成f(0) = 1
同样g(n-1) = 1
class Solution {
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
int [] dp1 = new int[length];//前缀积
int [] dp2 = new int[length];//后缀积
//初始化边界
dp1[0] = 1;
dp2[length-1] = 1;
//前缀积预处理
for(int i = 1;i<length;i++){
dp1[i] = dp1[i-1]*nums[i-1];
}
//后缀积预处理
for(int i = length-2;i>=0;i--){
dp2[i] = dp2[i+1]*nums[i+1];
}
for(int i = 0;i<length;i++){
nums[i] = dp1[i]*dp2[i];
}
return nums;
}
}
六、和为k的子数组
题目链接
这道题我们看到提示中说数组可能存在负数,因此就不具有单调性了,不能使用滑动窗口
暴力策略就是枚举所有子数组,看看有没有符合要求的,找到一个后不能停止枚举,因为可能还存在其他符合要求的子数组
我们可以利用前缀和思想
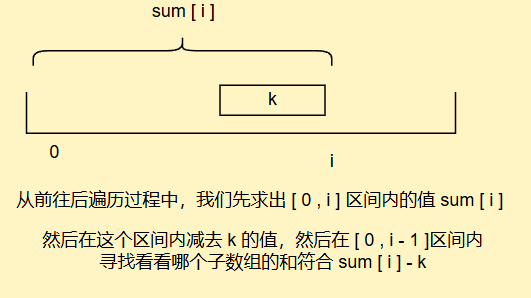
你说为什么不去[0,i]区间内寻找,因为你想,我们i下标的值就算很大,它减去了k值,那它是不是相当于把当前的位置占了,我们只能在子区间内寻找符合要求的值了
因此我们刚刚画的图k的范围可能很大,也可能没有
好,我们还要统计出现次数,我们可以利用哈希表统计,那么其下标映射关系<int,int>
第一个int表示前缀和的值,第二个int表示出现次数
好,我们来说说几个细节问题
-
前缀和什么时候进入哈希表
答:我们求当前下标符合要求的子数组,是不是要让哈希表只统计从0下标到我们当前下标区间内的前缀和出现次数
为什么要这么做,因为如果你统计的不是我们当前区间范围内的前缀和出现次数,当我们往后遍历数组的时候,会导致前面已经统计过了一次,现在又要统计一次,出现了重复统计
因此我们在进行计算完成统计好次数之后,准备往后遍历的时候,再把当前位置的前缀和放入就好 -
是否需要创建一个前缀和数组
答:不需要,我们不需要统计区间长度,只需要统计次数,因此我们用一个sum变量充当求和值就好 -
如果我们数组中的第一个值就是k呢
答:按照原理,那我们应该就要去[0,-1]区间内寻找,但是这就产生了越界情况
因此,我们默认前缀和为0的至少出现了一次,即hash<0,1>
class Solution {
public int subarraySum(int[] nums, int k) {
Map<Integer,Integer> hash = new HashMap<Integer,Integer>();
hash.put(0,1);
int sum = 0;
int ret = 0;
for(int x:nums){
sum += x;
ret += hash.getOrDefault(sum-k,0);
hash.put(sum,hash.getOrDefault(sum,0)+1);
}
return ret;
}
}
七、和可被k整除的子数组
题目链接
首先我们先来了解一下同余定理
假设有两个数,他们能被p整除,得到k这个结果
那么根据定理(a-b)%p=k,即a % p = b % p余数相等
这个定理证明可以去网上搜搜,这里就不详述了
在Java中我们负数取模会导致结果是负数,因此我们需要修正a%p+p,但是如果a本身就是正数,会导致我们重复计算,因此我们进行最后修正(a%p+p)%p
好,这一题还是利用前缀和以及哈希表统计次数
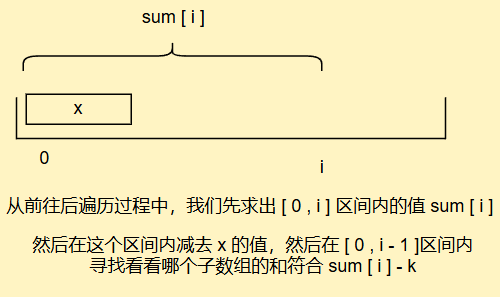
但是请注意,这一题并没有给我们区间x的值,因此它是一个随机变化的数,还记得我们刚刚的同余定理吗
我们代入这一题(sum - x) % k = 0 ---> sum % k = x % k
因此我们在求sum-x区间内的符合要求的子数组的时候,实质上就在求[0,i-1]区间内符合要求的子数组
因此我们的问题就转换成在[0,i-1]区间内寻找符合要求的子数组,使得2子数组的值总和能被k整除
因此我们创建的哈希表<int,int>,第一个int代表对应求的前缀和的余数,第二个int代表出现次数,其他还是不变,比如sum变量代表前缀和什么的
class Solution {
public int subarraysDivByK(int[] nums, int k) {
Map<Integer,Integer> hash = new HashMap<Integer,Integer>();
hash.put(0 % k,1);
int sum = 0;
int ret = 0;
for(int x : nums){
sum += x;
int r = (sum%k+k)%k;
ret += hash.getOrDefault(r,0);
hash.put(r,hash.getOrDefault(r,0)+1);
}
return ret;
}
}
八、连续数组
题目链接
这一题我们可以这么想,如果我们统计个数,会非常麻烦,因为你的区间是不断变化的,你的哈希表每次都要更新
但是,如果我们把0换成-1,假如区间内0和1个数对等,那么它们和就会为0
因此我们哈希表<int,int>,第一个int代表前缀和,第二个int代表对应的下标
其次,我们要等到i下标数值参与计算后,往后走的时候再放入哈希表
再者,如果出现前缀和重复的情况,你想,我们遍历是从前往后遍历
我们只有选择下标值更小的i,才可以使得i和j区间内所围成的长度最大
还有,关于计算长度,由于我们的j小标是包含在随机变量x里面的,因此我们的长度并不包括在内,因此我们的长度就是j+1~i,可以看我刚刚的图示
最后,关于我们的默认前缀和余数,它的值是0我们知道,但是它应该放入哪个下标呢?
答案是-1下标,为什么?这样在我们计算最长子数组的时候,就是求的0~i+1的长度了
class Solution {
public int findMaxLength(int[] nums) {
Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
hash.put(0, -1); // 默认存在⼀个前缀和为 0 的情况
int sum = 0, ret = 0;
for(int i = 0; i < nums.length; i++){
sum += (nums[i] == 0 ? -1 : 1); // 计算当前位置的前缀和
if(hash.containsKey(sum)){
ret = Math.max(ret, i - hash.get(sum));
}else{
hash.put(sum, i);
}
}
return ret;
}
}




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








