硅基计划4.0 算法 滑动窗口

一、长度最小的子数组
题目链接
这题意思就是我们在给出的数组内寻找一个连续的区间,让这个区间的和等于我们的目标值,而且还要使得区间长度最小
我们利用双指针算法,再给出一个变量,去统计我们left和right区间内的值
我们让right向后走,并且加上每次位置的值,加到sum中,直到这个sum值>=目标值10

因此我们不用让right向右走了,我们让left向右走一步,此时如果你的right回到left位置,是不是相当于把前面的数重新遍历了一遍
因此我们让right位置保持不动就好
此时我们的范围就发生了变化,像不像一个窗口在慢慢滑动呢?
好,那我们新的区间的sum和怎么求呢?其实很简单,我们之前不是求过从left到right区间的值吗
因为right位置并没有改变,仅仅只是left向右移了一步,因此我们减去之前left下标的值就好了
因此我们使用滑动窗口的四要素:双指针围成窗口,判断是否出窗口,是否进窗口,再更新我们想要的结果
这么讲太生硬,我们举个题目中的例子来讲吧
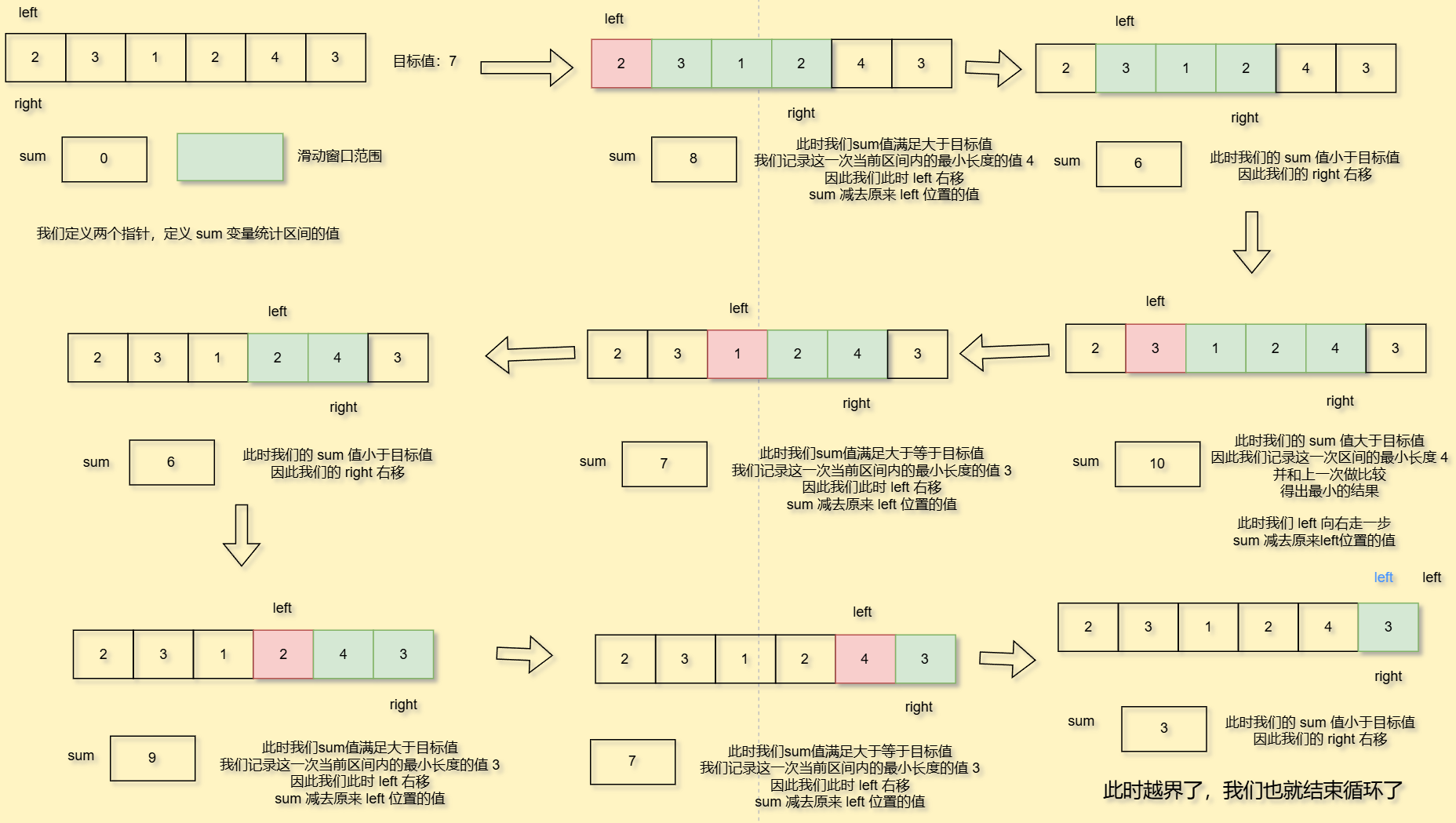
为什么说我们滑动窗口是正确的呢?刚刚你看我的过程讲解,也看的出来,我们是利用数字的单调性去解决问题
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0;
int right = 0;
int minLength = Integer.MAX_VALUE;
int sum = 0;
while(right < nums.length){
sum += nums[right];
while(sum >= target){
//检查最小长度是不是比最开始的还要小
minLength = Math.min(minLength,right-left+1);
sum -= nums[left];
left++;
}
right++;
}
return minLength == Integer.MAX_VALUE ? 0 : minLength;
}
}
时间复杂度:遍历一次n,最坏移动n次,总共2n次,即O(
n
2
n^2
n2)
二、无重复字符的最长子串
我们利用一个例子来讲解这个滑动窗口原理
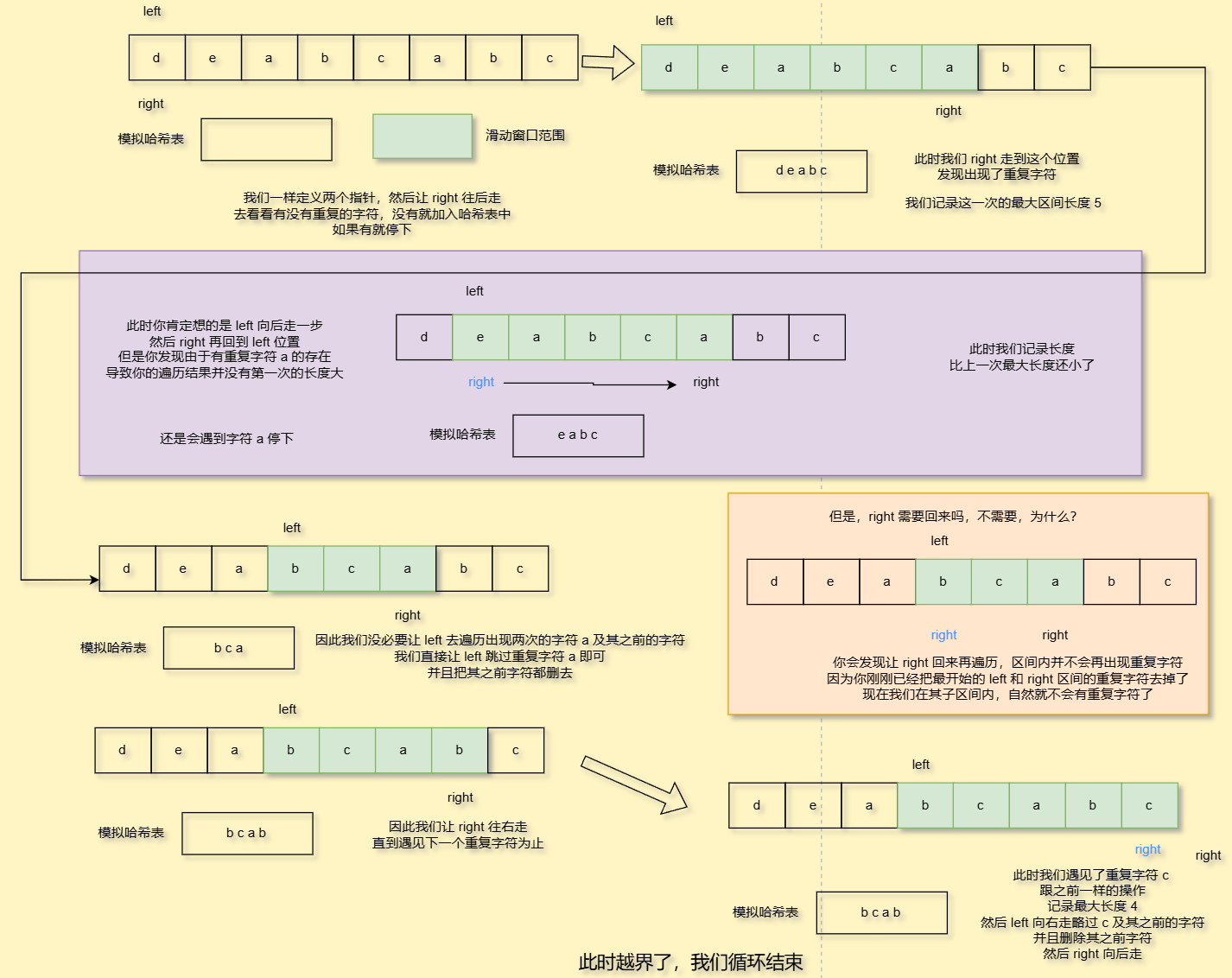
我们可以使用数组去模拟哈希表,让其下标对应字符ASCII码值,统计每个字符出现次数就好
class Solution {
public int lengthOfLongestSubstring(String s) {
int [] hash = new int[128];
int left = 0;
int right = 0;
int maxLength = 0;
while(right < s.length()){
//进入窗口,直到遇到重复字符为止
hash[(int)s.charAt(right)]++;
//右指针遇到重复字符了,左指针字符离开哈希表,并且左指针++
while(hash[(int)s.charAt(right)] > 1){
hash[(int)s.charAt(left)]--;
left++;
}
//结果取最大值
maxLength = Math.max(maxLength,right-left+1);
//判断完成后,右指针继续往后走
right++;
}
return maxLength;
}
}
三、最大的连续1的个数
题目中说的翻转就是把0变成1的意思
最多不超过K个,说的是可以翻转0~K个0变成1
如果你的k值很大,超过了数组长度,其实我们只需要返回这个数组长度就好了
我们还是利用题目实例去讲解原理
这道题的核心就是统计区间内0的个数,让其不能超过k个
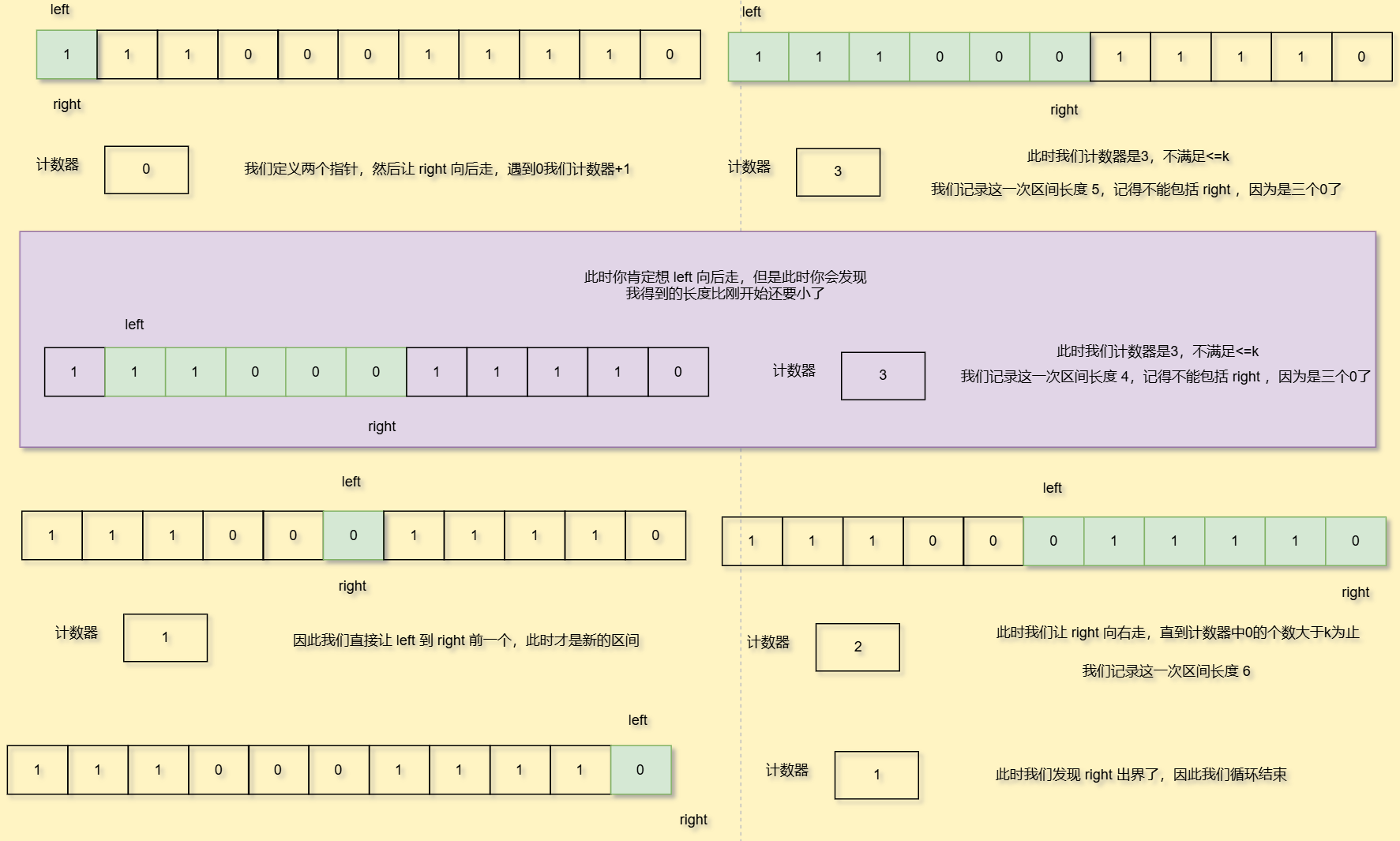
class Solution {
public int longestOnes(int[] nums, int k) {
int left = 0;
int right = 0;
int maxLength = 0;
int count = 0;
while(right < nums.length){
//遇见0计数器加加,进窗口操作
if(nums[right] == 0){
count++;
}
//只有区间内0的个数大于k个才进来,进行出窗口操作
while(count > k){
if(nums[left] == 0){
count--;
}
left++;
}
//更新最大值
maxLength = Math.max(maxLength,right-left+1);
//为什么放在最后++,因为只要区间内0的个数不超过k个,就是一个合法区间
right++;
}
return maxLength;
}
}
四、将x减小到0的最小操作数
题目链接
这个题目意思就是使用完一次数值过后,我们要删除改数值
其实我们可以这么想,我们去在该数组内选择一个区间(子数组),让这个区间的数恰好等于数组总和前期删去的左右数值

因此就跟我们的滑动窗口思想一样,right向后走,left不用回来
当我们子数组内的值总和等于我们原始数组总和减去目标值的时候,说明就找到了一个符合要求的区间,我们记录下值就好
class Solution {
public int minOperations(int[] nums, int x) {
int sum = 0;
for(int n:nums){
sum += n;
}
int target = sum-x;
if(target < 0){
return -1;
}
int left = 0;
int right = 0;
int count = 0;
int len = -1;
while(right < nums.length){
count += nums[right];
while(count > target){
count -= nums[left];
left++;
}
if(count == target){
len = Math.max(len,right-left+1);
}
right++;
}
return len == -1 ? -1 : nums.length-len;
}
}
五、水果成篮
题目链接
这道题看起来很复杂,其实核心就这么几个
- 每个数组内不同数字代表不同水果种类
- 每次只能选两种,当碰到第三种就停止,每次移动从数组左边向右边移动
- 一个篮子装一种水果
- 统计我们在数组内的子数组,保证内部只能出现两种水果,还要说最长的子数组即可
其实就是在数组中找一个连续的区域,使得区域内部最多只能有两种类型水果(可能为一种,也可能为两种),并且使得这个子数组的长度最长
因此我们可以借助哈希表去统计,如果这个哈希表中水果的种类个数大于2,我们就停止操作
我们就统计这个位置之前的区间长度就好

因为这一题的特殊性,我们知道题目中水果种类是小于数组大小的,因此我们使用模拟哈希表大大降低时间复杂度
class Solution {
public int totalFruit(int[] fruits) {
//不用哈希表,我们去模拟,时间复杂度就小很多
int len = fruits.length;
//len+1为了避免非法越界问题
int [] hash = new int[len+1];
int left = 0;
int right = 0;
//统计水果种类
int kinds = 0;
int maxCount = 0;
while(right < len){
//先判断是不是新的水果
if(hash[fruits[right]] == 0){
kinds++;
}
hash[fruits[right]]++;
//水果种类大于2进行出窗口操作
while(kinds > 2){
hash[fruits[left]]--;
//减到0水果种类就减少
if(hash[fruits[left]] == 0){
kinds--;
}
left++;
}
maxCount = Math.max(maxCount,right-left+1);
right++;
}
return maxCount;
}
}
六、找出字符串中所有字母异位词
题目链接
什么是异位词?指的就是改变字符串内部排序,但字符个数不变
比如"abc",它的一个异位词可以是"bca","cba"等等
那在题目给的字符串中找是什么意思呢?
比如题目给的是"cbaebabacd",目标字符串是"abc",那它所有的异位字符串有"cbaebabacd"
它们的起始下标分别是0和6,因此我们返回0和6
但也有可能有多种组合,比如题目给的是"abab",目标字符串是"ab"
那它的所有异位字符串有"ab,ba,ab",起始下标分别是0,1,2,因此返回0,1,2
这题可以使用暴力解法,也就是求出目标字符串长度,然后放入哈希表
再在题目给的字符串中寻找跟目标字符串长度一样的子串,然后放入哈希表进行对比就好
之后继续在题目的字符串中向后枚举
但是这样太复杂了,我们来看看如何优化
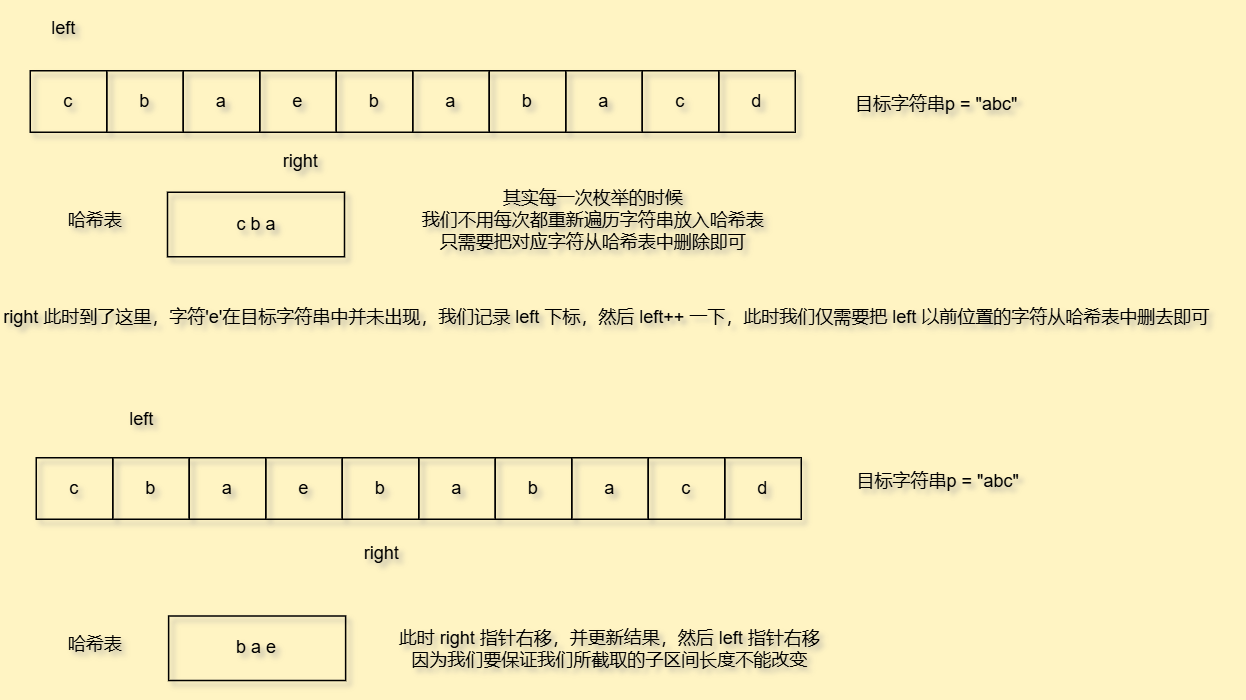
好,但是我们去比较两个哈希表的时候,如果使用遍历一个个比较,未免太麻烦了
因此我们要使用一个变量count去统计有效字符个数
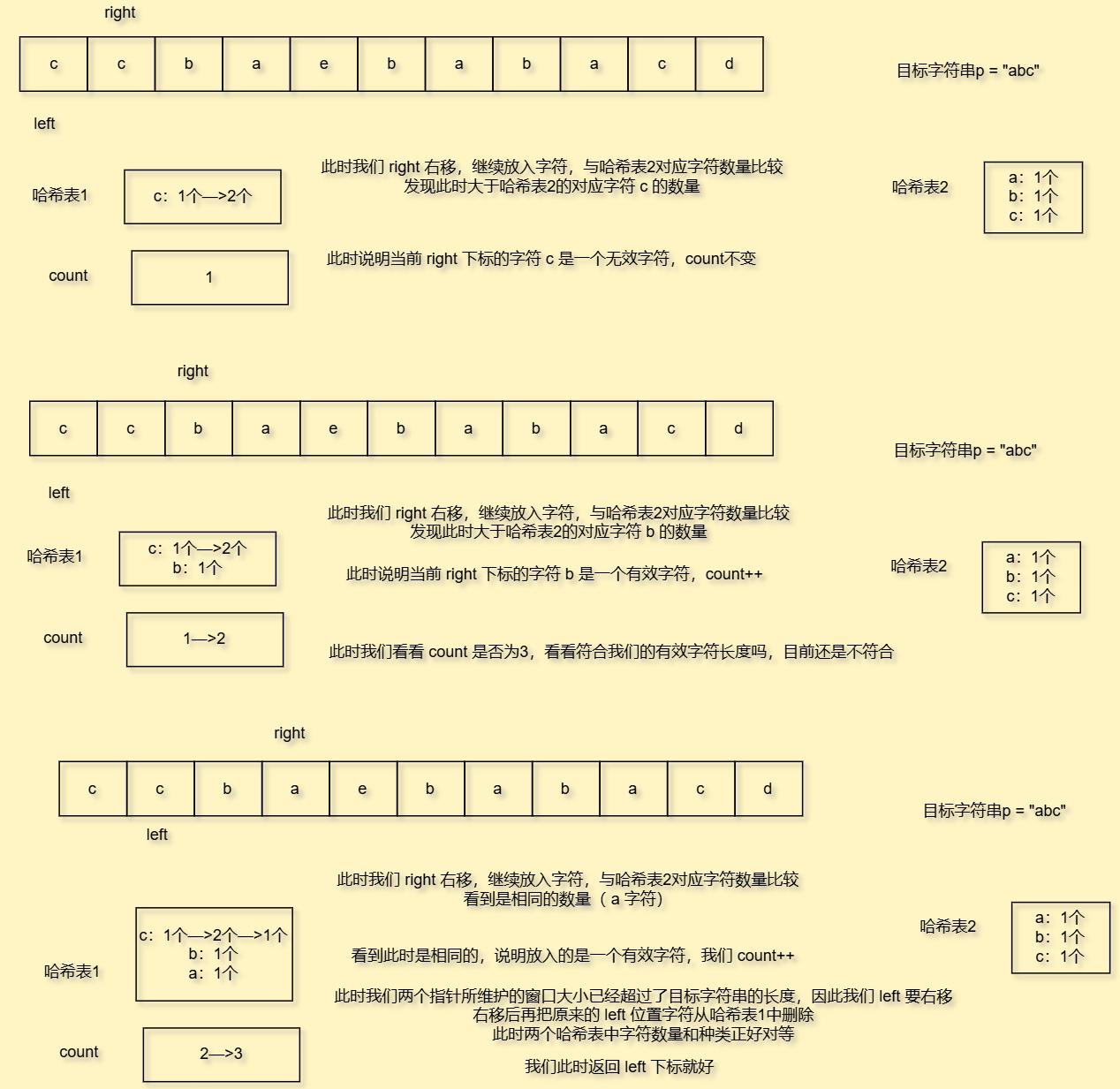

因此对应变量count
- 进窗口时要与目标字符串所在地哈希表对应字符的数量进行比较,看看是否小于,如果小于,说明是一个有效字符,
count++;否则count不变 - 出窗口之前,我们看看当前字符在目标字符串的哈希表中对应字符数量,如果小于等于目标字符串对应的字符数量,说明你删去的是一个有效字符,
count要减减;否则count不用变化 - 当
count == 目标字符串长度的时候进行判断,输出left下标即可
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer>list = new ArrayList<>();
char [] ss = s.toCharArray();
char [] pp = p.toCharArray();
int [] hash1 = new int[26];//存s字符串信息,即窗口
int [] hash2 = new int[26];//存p字符串信息
//存p字符串进入哈希表
for(char ch:pp){
hash2[ch-'a']++;
}
int left = 0;
int right = 0;
int count = 0;
while(right<ss.length){
char chs1 = ss[right];
hash1[chs1-'a']++;
//进窗口判断
if(hash1[chs1-'a'] <= hash2[chs1-'a']){
count++;
}
if(right-left+1>pp.length){
char chs2 = ss[left];
left++;
//出窗口判断
if(hash1[chs2-'a'] <= hash2[chs2-'a']){
count--;
}
hash1[chs2-'a']--;
}
if(count == pp.length){
list.add(left);
}
right++;
}
return list;
}
}




















 811
811

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








