作者本科毕业设计是做机器人轨迹跟踪控制,轨迹由函数曲线来描述,本文选取三阶贝塞尔曲线为代表进行讲解,并展示部分基于Python Tkinter的实现代码。
首先简单了解一下什么是贝塞尔曲线(余弦函数曲线我就不多说了哈!),贝塞尔曲线又称贝兹曲线,是法国工程师皮埃尔.贝塞尔于1962年发表。贝塞尔曲线广泛应用于二维绘图软件,早期用于汽车车体设计。
三阶贝塞尔曲线由如下方程描述:
其中t的范围是0到1的闭区间。P0和P3是三阶贝塞尔曲线的起点和终点,P1和P2是曲线的控制点。
然后我们讲一下计算机绘制曲线的原理。从数学定义上,一条连续函数曲线有无数个点,从算法的特点将,算法具有有穷性。所以我们不可能把所有的点全部刻画在屏幕上。另一方面,计算机的屏幕像素是离散的,无法表示连续的曲线。于是引入一个概念,那就是微分思想。将曲线分为一个个小段,将曲线“化曲为直”。
最后说明一下计算机屏幕的坐标系。数学里的笛卡尔坐标系通常以水平向右为x轴正方向,垂直于x轴向上为y轴正方向。而计算机屏幕表示像素点时,其坐标原点位于屏幕左上角,x轴水平向右,而y轴垂直于x轴向下。
下面展示贝赛尔曲线函数代码:
def tri_bezier(p1,p2,p3,p4,t):
parm_1 = (1-t)**3
parm_2 = 3*(1-t)**2 * t
parm_3 = 3 * t**2 * (1-t)
parm_4 = t**3
px = p1[0] * parm_1 + p2[0] * parm_2 + p3[0] * parm_3 + p4[0] * parm_4
py = p1[1] * parm_1 + p2[1] * parm_2 + p3[1] * parm_3 + p4[1] * parm_4
return (px,py)
效果展示:
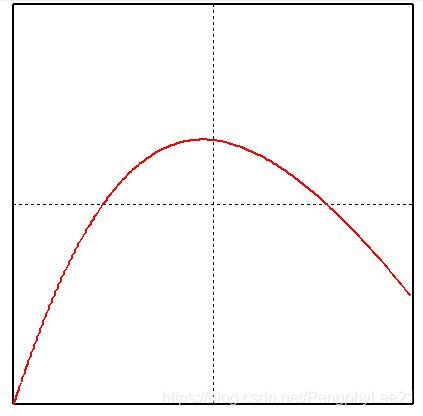
以上图像没有进行屏幕坐标系向笛卡尔坐标系转换,具体如何通过Tkinter库实现,后面我会更新博客,敬请期待!才疏学浅,难免有错误疏漏之处,还请各位大佬提出指正!





 本文介绍三阶贝塞尔曲线在机器人轨迹跟踪控制中的应用,详细解释了贝塞尔曲线的概念及其在计算机屏幕上的绘制原理,展示了使用Python实现的贝塞尔曲线函数。
本文介绍三阶贝塞尔曲线在机器人轨迹跟踪控制中的应用,详细解释了贝塞尔曲线的概念及其在计算机屏幕上的绘制原理,展示了使用Python实现的贝塞尔曲线函数。
















 1383
1383

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








