【Python】Bezier曲线的绘制

小周ipython

已于 2022-05-20 20:36:52 修改

阅读量2.3k

点赞数 5

分类专栏： CAGD 文章标签： python 几何学

于 2022-05-07 09:08:34 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_45718987/article/details/124623306

版权

CAGD 专栏收录该内容

13 篇文章

订阅专栏

Bezier曲线的绘制

$\sum_i{J_{n,i}(u)V_i}$
$J_{n,i} = C^i_nu^i(1-u)^{n-i}$

1. 方法

输入n作为Bezier曲线的次数
手动在画布上点击n+1个点（未实现，采用了手动输入坐标点）
绘制控制多边形，即相邻两个点之间用直线连接
通过Bezier曲线函数绘制曲线

2. 导入相关程序包

# 导入相关包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import xticks,yticks
import math
import random

plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

3. 修改定义Bernstein基函数

Bernstein基函数绘制可见https://blog.youkuaiyun.com/weixin_45718987/article/details/124584407?spm=1001.2014.3001.5502

# 阶乘函数
def jc(x):
    return math.factorial(x)

def Bernstein(n,m): 
    u = np.linspace(0,1,m)  # m代表[0,1]上取多少个点
    J = pd.DataFrame() # 存储伯恩斯坦基函数的值
    for i in range(n+1):
        k = i
        column = 'C'+str(i)
        C_nk = jc(n)/(jc(k)*jc(n-k))
        J_nk = C_nk*pow(u,k)*pow(1-u,n-k)
        J[column] = J_nk
    return J

4. 定义Bezier曲线函数

# 输入n
def Bezier():
    n = int(input("请输入n（n为Bezier次数）："))
    m = int(input("请输入m（m为u的取值个数）："))
    x = []
    y = []
    for i in range(n+1):
        x1 = float(input("请输入第{0}个点的x坐标：".format(i+1)))
        y1 = float(input("请输入第{0}个点的y坐标：".format(i+1)))
        print("添加坐标点({0},{1})\n".format(x1,y1))
        x.append(x1)
        y.append(y1)
    J = Bernstein(n,m)

    # x = [1,2,3,4,5,6,7,7]
    # y = [1,1.5,1.5,0.5,0.5,1,0.8,0]

    X_bez = []
    Y_bez = []
    for i in range(m):  
        a = sum(J.iloc[i,:]*list(x))  # x为所有点x轴的值
        b = sum(J.iloc[i,:]*list(y))  # y为所有点y轴的值
        X_bez.append(a)
        Y_bez.append(b)

    # 绘制Bezier曲线
    fig = plt.figure(figsize=(10,8))
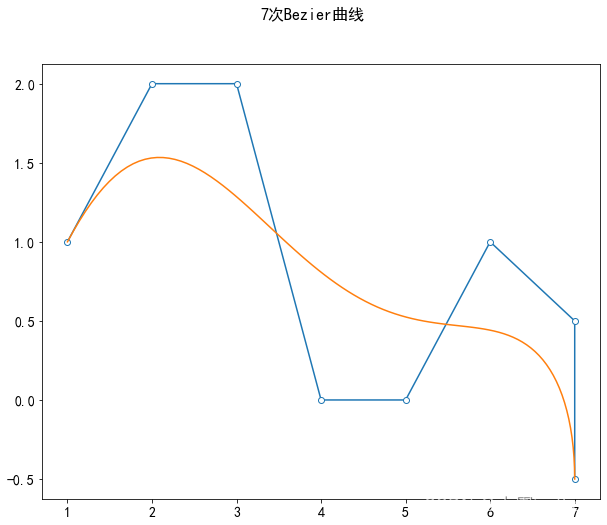
    fig.suptitle(str(n)+'次Bezier曲线',fontsize=16)
    plt.plot(x,y,marker='o',markerfacecolor='white')  # 画空心圆
    plt.plot(X_bez,Y_bez)  # 画空心圆
    plt.xticks(fontsize=14)
    plt.yticks(fontsize=14)
    # plt.axis([-1,8,-0.2,2])
    # plt.xticks(np.linspace(0,10,11))
    # plt.yticks(np.linspace(0,5,11))
    plt.show()

5. Bezier()函数调用绘制曲线

Bezier()

请输入n（n为Bezier次数）：7
请输入m（m为u的取值个数）：100
请输入第1个点的x坐标：1
请输入第1个点的y坐标：1
添加坐标点(1.0,1.0)

请输入第2个点的x坐标：2
请输入第2个点的y坐标：2
添加坐标点(2.0,2.0)

请输入第3个点的x坐标：3
请输入第3个点的y坐标：2
添加坐标点(3.0,2.0)

请输入第4个点的x坐标：4
请输入第4个点的y坐标：0
添加坐标点(4.0,0.0)

请输入第5个点的x坐标：5
请输入第5个点的y坐标：0
添加坐标点(5.0,0.0)

请输入第6个点的x坐标：6
请输入第6个点的y坐标：1
添加坐标点(6.0,1.0)

请输入第7个点的x坐标：7
请输入第7个点的y坐标：0.5
添加坐标点(7.0,0.5)

请输入第8个点的x坐标：7
请输入第8个点的y坐标：-0.5
添加坐标点(7.0,-0.5)

在这里插入图片描述

6. 通过鼠标click方法在画布上选取坐标点方法

封装为class，因为class中全局变量方便使用；
matplotlib中交互取点的方法是用canvas.mpl_connect，其下有许多鼠标或键盘的画布取点响应方式；
class中定义函数，注意添加self，用来继承类中的方法和对象，在类中一个函数func1(self)调用另一个函数func2(self)需要采用格式：self.func2()；
下面将1-5的Bezier曲线绘制封装至class中，并在类中定义鼠标取点方法

import matplotlib.pyplot as plt
import numpy as np
from numpy.random import rand
import pandas as pd
import math
import random

plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

class click_curve:
    # 在类中定义的带self的变量均为全局变量
    def __init__(self,n,m,ax):
        self.ax = ax
        self.m = m
        self.n = n
        self.x = []
        self.y = []
        self.i = 0
        self.cid = self.ax.figure.canvas.mpl_connect('button_press_event', self)

    def jc(self,a):  # 阶乘
        return math.factorial(a)

    def Bernstein(self): 
        u = np.linspace(0,1,self.m)  # m代表[0,1]上取多少个点
        J = pd.DataFrame() # 存储伯恩斯坦基函数的值
        for i in range(self.n+1):  # 输入n个点，n不为次数
            k = i
            column = 'C'+str(i)
            C_nk = self.jc(self.n)/(self.jc(k)*self.jc(self.n-k))
            J_nk = C_nk*pow(u,k)*pow(1-u,self.n-k)
            J[column] = J_nk
        return J
    
        # 输入n
    def Bezier(self):
        # 调用Bernstein基函数
        J = self.Bernstein()
    
        X_bez = []
        Y_bez = []
        for i in range(self.m): 
            a = sum(J.iloc[i,:]*list(self.x))  # x为所有点x轴的值
            b = sum(J.iloc[i,:]*list(self.y))  # y为所有点y轴的值
            X_bez.append(a)
            Y_bez.append(b)
        self.ax.plot(self.x,self.y,'b')  # 连线
        self.ax.plot(X_bez,Y_bez,'r')  # 画曲线
        print('success')
        self.ax.figure.canvas.draw()
    
    def __call__(self,event):
        if event.inaxes != None:
            if event.button==1 and self.i < self.n+1:
                self.i+=1
            #     plt.ax.scatter(event.xdata, event.ydata)
                self.x.append(event.xdata)
                self.y.append(event.ydata)
                print("输入坐标点为：({0:.2f},{1:.2f})".format(event.xdata, event.ydata))
                self.ax.plot(event.xdata, event.ydata, 'bo',markerfacecolor='white')
                self.ax.text(event.xdata+0.05, event.ydata+0.05,"({0:.2f},{1:.2f})".format(event.xdata, event.ydata))
                self.ax.figure.canvas.draw()
            elif self.i >= self.n+1:
                print("绘图结束")
                print("x取值：{0}".format(self.x))
                print("y取值：{0}".format(self.y))
                self.Bezier()
                print("end")
            return
        else:
            print("出界了")
            
    # def click1(self):
    #     self.ax.figure.canvas.mpl_connect('button_press_event', self.click)
    

            
def main():    
    n = int(input("请输入次数："))
    x = input("请输入你希望的X轴区间(用空格隔开)：").split(" ")
    y = input("请输入你希望的Y轴区间(用空格隔开)：").split(" ")
    m = int(input("请输入m（m为u的取值个数）："))
    print("\n请在画布上依次点击{0}个点".format(n+1))
    x1 = []
    y1 = []
    for i in range(len(x)):
        x1.append(int(x[i]))
        y1.append(int(y[i]))
    
    fig = plt.figure()
    ax1 = fig.add_subplot(111)
    plt.xlim(x1[0],x1[1])
    plt.ylim(y1[0],y1[1])
    plt.title("{0}次Bezier曲线".format(n))
    plt.yticks(fontsize=14)
    plt.xticks(fontsize=14)
    click_curve(n,m,ax1)
    # test.click1()
    plt.show()
    
if __name__ == '__main__':
    main()

取 $x\in[0,5],y\in[0,5],m=100$ ，得到绘图过程图如下所示：

请输入次数：3

请输入你希望的X轴区间(用空格隔开)：0 5

请输入你希望的Y轴区间(用空格隔开)：0 5

请输入m（m为u的取值个数）：100

请在画布上依次点击4个点
输入坐标点为：(0.70,1.80)
输入坐标点为：(1.67,3.84)
输入坐标点为：(3.73,3.94)
输入坐标点为：(2.47,2.84)
绘图结束
x取值：[0.6955645161290323, 1.6733870967741937, 3.729838709677419, 2.469758064516129]
y取值：[1.7980011531808577, 3.8435243403530928, 3.939622745119574, 2.841355262074078]
success
end

交互取点

在这里插入图片描述