向量积（叉乘）

两个 向量 a和 b的叉积写作 a× b（有时也被写成 a∧ b，

避免和字母x混淆）。向量积可以被定义为：

|向量 a×向量 b|=| a|| b|sinθ在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。

这个定义有一个问题，就是同时有两个单位向量都垂直于积：若满足垂直的条件，那么也满足。

一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从 a以不超过180度的转角转向 b时，竖起的大拇指指向是 c的方向。

向量积 |c|=|a×b|=|a| |b|sin<a,b>

即 c的长度在数值上等于以 a， b，夹角为θ组成的平行四边形的面积。

c的方向垂直于a与b所决定的平面，c的指向按右手规则从a转向b来确定。

设

   

=(

   

)，

   

=(

   

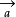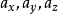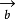)。i，j，k分别是X，Y，Z轴方向的单位向量，则：

a× b=(

   

-

   

) i+(

   

-

   

) j+(

   

-

   

) k,为了帮助记忆，利用三阶 行列式，写成det

 

b× a= - a× b右手规则

三角形ABC的面积=

   

[2] 

matlab代码：cross（a,b)