解题思路-leetcode第五十二题：N皇后Ⅱ

解题思路-leetcode第五十二题：N皇后Ⅱ

题目描述：
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

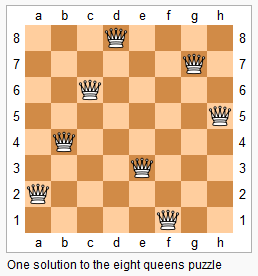
上图为 8 皇后问题的一种解法。
给定一个整数 n，返回 n 皇后不同的解决方案的数量。
示例:
输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],
["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
提示：
皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一或七步，可进可退。（引用自 百度百科 - 皇后 ）
解题思路：本题上51题N皇后几乎没有区别，无非是一个返回所有的解，一个返回所有解的个数，所以本题在51题的基础上将代码中的返回值改成了存储所有解的列表的长度。代码如下：

class Solution:
    def totalNQueens(self, n: int) -> int:
        ans = list()
        res = [['.']*n for i in range(n)]
        l = [True] * n
        d = [True] * (2*n - 1)
        fd = [True] * (2*n - 1)
        def dfs(u):
            list_1 = list()
            if u == n:
                for i in range(n):
                    list_1.append(''.join(res[i]))
                ans.append(list_1)
                return
            for i in range(n):
                if l[i] and fd[u+i] and d[n-1-u+i]:
                    res[u][i] = 'Q'
                    l[i] = fd[u+i] = d[n-1-u+i] = False
                    dfs(u+1)
                    res[u][i] = '.'
                    l[i] = fd[u+i] = d[n-1-u+i] = True
        dfs(0)
        return len(ans)

提交后，通过。
此处放上51题的链接：51题-N皇后