游戏中的随机值-高斯随机值、随机筛选值、柏林噪声

为了使游戏增加丰富度，不断给玩家新鲜感，很多时候我们都需要用到随机值。下面介绍三种高级的随机值技术，在某些场景下，他们比rand()表现更好。

一、高斯随机值

在日常生活中，我们的身高，体重和智商、运动员奔跑的速度，市区的房价，都满足正态分布（高斯分布）。在游戏中同样如此，比方说我们需要模拟一名射击手打靶：

作为一名专业的射击，显然右侧的更接近真实状况。要不然怎么参加比赛啊。
那么我们用函数怎么取到高斯随机值呢。
根据中央极限定理，对[-1,1]范围内均匀随机求和，那么我们的取值结果会逼近0，标准差为√k/3的正态分布。K为参与求和的随机值数量。比如我们每次取三个数求和，那么标准差是1，就是一个标准的正态分布。

下面的函数取[-3,3]之间随机3个数相加，通过伪随机数生成器使用异或位移操作产生均匀随机数。
66.7%的位于在一个标准差范围内，95.8%的位于在两个标准差范围内，100%的值位于三个标准差范围内。

unsigned long seed = 61829450;
double GaussianRand()
{
	double sum = 0;
	for (int i = 0; i < 3; i++)
	{
		unsigned long holdseed = seed;
		seed ^ = seed << 13;
		seed ^ = seed >> 17;
		seed ^ = seed << 5;
		long r = (Int64)(holdseed + seed);
		sum + = (double)r * (1.0/0x7FFFFFFFFFFFFFFF);
	}return sum; 
	//returns [-3.0, 3.0] at (66.7%, 95.8%, 100%)
}

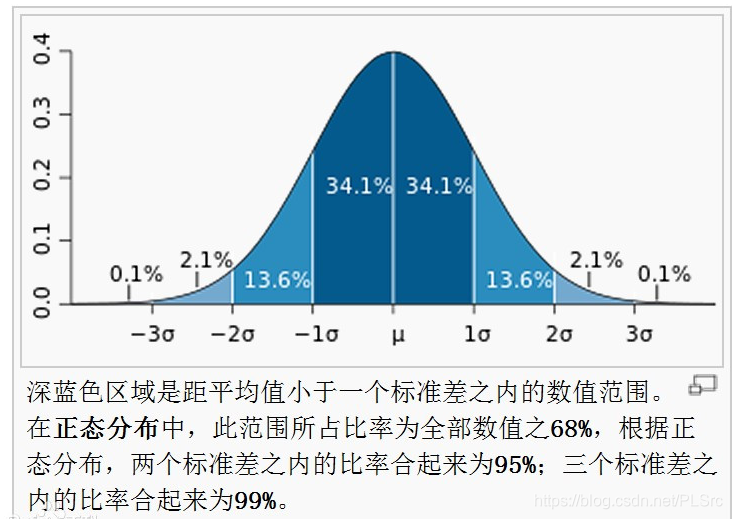
尽管真实的正态分布，后面的尾部会延伸很远，但是游戏中这样的正态分布足够我们使用。

下面再返回那个射击手打靶，这里的方法是在极坐标上混合使用均匀分布和高斯分布。首先，应为角度可以取均匀随机，那我们现在0-360°中取一个值作为相对于中心点的角度。然后再用高斯分布取一个到中心的距离。这样取出来的值就可以真实模拟射击情况。

高斯分布在游戏中可以用到的地方：

• 平均或最大速度
• 体型、宽、高、质量
• 反应时间
• 射击频率，上子弹频率
• 技能冷却时间
• 暴击概率

假如有几十个士兵共同射击，当每个士兵射击频率取高斯随机值时，呈现将非常自然，而不是同时开枪同时射击。

二、随机值筛选

这种随机值时为了防止因为“太随机”而进行应对的方法。所谓太随机比如我们丢一枚硬币，连续十次出现正面也是很有可能的，但放在游戏中，把硬币换成暴击，换成开箱子。连续的没有正反馈，玩游戏的玩家会认为是不是你在背后操控数值，从而对游戏失去信任，感觉被欺骗（其实我们没做手脚）。下面就是几种应对策略：

1.识别异常

1.111000,11001100
2.010100000001
这两种情况会被认为不自然，当满足规则后将最后一个数剔除。规则取决于生成随机数类型。

1.1二元随机数筛选

当数值元素像硬币一样为50%的概率，我们可以依照以下规则
1.当生成的数导致长度为4或者更长，有70%的概率翻转改值。这条规则不会完全清除4以上序列，但会将其可能性一步步压小。
2.出现11001100，则翻转最后一个数为11001101。
3.出现111000或者000111，翻转最后一个数。

1.2筛选整数范围

下面是一组较为严格的规则，出现后重新生成随机数
1.数字重复出现77,88
2.间隔出现565,232
3.长度等于4的递增4567
4.N个数出现过多个位于范围内底部或顶部的数字29381939
5.两数字在最近10个重复出现236932
6.特定数字重复出现614695686

1.3筛选浮点数范围

筛选[0,1]的浮点数，避免近似数集中出现，还有避免长段的递增递减。如果违反规则，生成新随机数。
1.连续两个数的差小于0.02，0.362,0.351
2.连续3个数差小于0.1比如0.326,0.251,0.123
3.连续五个数出现递减或者递增
4.N个数出现过多位于底部或顶部的数字

1.4筛选高斯随机数范围

高斯数和浮点数接近，但可以加几条应对特殊情况
5.连续出现4个大于0或者小于0的数
6.连续出现4个位于第二标准差或者第三标准差的数
7.连续出现两个位于第三标准差的数

1.5随机完整性

前面的规则都是较为主观的规则，实际使用可以更严格或者更宽松。但严格的规则可能会导致对结果的推测，所以要适度。

2.实现细节

对于随机数的生成，我们要尽量保持独立。比如攻击敌方的暴击率不受对方暴击率的影响。
对不同的场景使用不同的规则可以产生不同的效果。
比如我们可以让玩家在锻造时产生欧皇的感觉，扑克牌的好牌型出现频率更高等，提升玩家体验。
也可以严格控制连续暴击的情况。

三、用于游戏AI的柏林噪声

上图为柏林噪声在图形学的应用。我们可以通过这种效果生成烟雾，云彩，火焰等。柏林噪声并不属于均匀分布，也不属于正态分布。而是连贯随机性，连续生成的随机数之间相关。意味着我们不会再得到一个小的随机数后下一个突然出现一个很大的随机数。
下面是柏林噪声在AI的潜在应用：

• 角色移动，方向速度加速度
• 动画叠加层
• 精准度 连续成果或者失败，保持良好状态，运气值
• 注意力 守卫警惕程度
• 行为风格 防御型，进攻型
• 角色情绪

明天再写
本文是《游戏人工智能的笔记》感兴趣可以买书去看