数值分析的LU分解法
本网所有内容文字、图片和音视频资料,版权均属个人所有,仅供个人呢学习参考,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他方式复制发布/发表。
最近学习,以下是个人心得体会:(这里重点讲如何解题)
1.简介:
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。LU分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。
2.原理:
LU分解是基于高斯消元法的,消去法就是核心。
3.解题:
这里我们抛开书中复杂的公式和定理,教给大家一种简单的消元法:
以书中例题4-2为例:
设
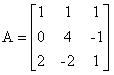
对矩阵A进行LU分解。
解:
- 首先在3*3矩阵上,需要先分解出U矩阵,再分解L矩阵。
- 对于上三角U来说,可以采用第一行为基准,对矩阵做行变换,消去下三角部分元素:
- 矩阵U化简步骤如下:
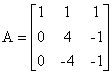**.](https://img-blog.csdnimg.cn/20191105222946869.png)
矩阵](https://i-blog.csdnimg.cn/blog_migrate/457fd8514dc80a66e7be508a666e9a4c.png)
- 对于下三角L来说,可以采用第一列为基准,对矩阵做行列变换,消去上三角部分元素:
(另:L必须保证主对角线为单位阵) - 矩阵L化简步骤如下:
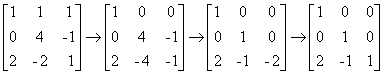
L化简必须保证最后主对角线为单位阵。 - 此时分解完毕。
补充说明:
另有需要求解方程组(X,Y值)的题目,前面道理相同,先算出U矩阵,行变换结束的同时可以解得Y值。
因为
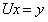
所以
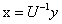
带入计算即可。
如有不对之处,请批评指正。
数值分析介绍
数值分析是数学的一个分支,主要研究使用数值计算方法解决数学问题的领域。以下是关于数值分析的详细解释:
- 定义与目的:
数值分析是研究用计算机求解数学计算问题的数值计算方法及其理论的学科。
数值分析的目的在于设计及分析一些计算的方式,可针对一些问题得到近似但够精确的结果。 - 应用领域:
数值分析在现代科学和工程领域中有着广泛的应用,包括但不限于:
工程领域:结构力学、电力系统、流体力学等。
金融领域:股票价格预测、风险评估、期权定价等。
自然科学领域:物理、化学、生物等。 - 主要方法:
直接法:利用固定次数的步骤求出问题的解,如高斯消去法、QR算法、单纯形法等。
迭代法:通过从一个初始估计出发寻找一系列近似解来解决问题的数学过程,如牛顿法、二分法、雅可比法等。迭代法通常用于求解大型矩阵代数问题。 - 数值分析算法:
方程组求解:高斯消元法、LU分解法等。
矩阵运算:矩阵乘法、矩阵求逆、特征值和特征向量计算等。
函数积分:数值积分方法(如梯形法则、辛普森法则)和自适应积分等。 - 离散化:
在数值分析中,经常需要将连续模型的问题转换为一个离散形式的问题,以便使用数值方法求解。这个过程称为离散化。 - 工具与软件:
MATLAB:用于数据分析、无线通信、图像处理等领域。
SPSS:统计产品与服务解决方案软件。
Excel:电子表格和数据处理软件,提供数据处理和分析功能。
R:统计计算和图形化软件环境,具有强大的数据分析能力。
Tableau:功能强大的数据可视化工具,提供丰富的可视化选项。
Python(NumPy、SciPy):提供高性能的数值计算功能,以及各种优化和拟合函数。
SAS:专门用于统计分析和数据挖掘的商业软件。 - 数值分析的重要性:
数值分析为科学和工程领域提供了强大的计算工具,使得复杂问题的求解成为可能。
数值分析方法的准确性和效率直接影响到科学研究和工程设计的成果。
综上所述,数值分析是一个广泛应用于各个领域的数学分支,它通过研究和应用数值计算方法,为科学和工程领域提供了强大的计算支持。
lU分解法的程序实现
LU分解法(也称为LU因式分解)是数值分析中用于求解线性方程组Ax = b的一种有效方法。LU分解将一个方阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积,即A = LU。这种方法在求解线性方程组时特别有用,因为它允许我们通过前向替换和反向替换两个步骤来求解,而不是直接对原矩阵A进行求逆。
LU分解的基本步骤如下:
通过高斯消元法(带部分选主元)将矩阵A转换为上三角矩阵U。
在这个过程中,记录对A的行所做的所有操作(即乘法和加法),并将这些操作应用于单位矩阵I,从而得到下三角矩阵L。
在Python中,我们可以使用NumPy库中的numpy.linalg.lu函数来执行LU分解。但是,为了更清楚地展示LU分解的过程,我们可以手动实现它(尽管这通常不如使用优化过的库函数高效)。
下面是一个简单的LU分解的Python实现示例:
import numpy as np
def lu_decomposition(A):
n = A.shape[0]
L = np.eye(n) # 初始化L为单位矩阵
U = A.copy() # 初始化U为A的副本
# 高斯消元法(带部分选主元)
for k in range(n - 1):
# 部分选主元:找到当前列中绝对值最大的元素所在的行
max_index = np.argmax(np.abs(U[k:, k])) + k
U[[k, max_index], k:] = U[[max_index, k], k:] # 交换行
L[[k, max_index], :] = L[[max_index, k], :] # 相应地更新L
# 更新L和U
for i in range(k + 1, n):
factor = U[i, k] / U[k, k]
U[i, k:] -= factor * U[k, k:]
L[i, :k+1] -= factor * L[k, :k+1]
return L, U
# 示例矩阵
A = np.array([[4, 3], [6, 3]], dtype=float)
L, U = lu_decomposition(A)
print("L:")
print(L)
print("U:")
print(U)
请注意,这个简单的实现没有处理一些特殊情况,如当主元为0时(这在实际应用中通常通过部分选主元或完全选主元来避免)。此外,这个实现也没有进行任何数值稳定性优化,因此在实际应用中,建议使用经过优化的库函数(如NumPy的numpy.linalg.lu)来进行LU分解。




 本文深入讲解了数值分析中的LU分解法,介绍了其基本原理、解题步骤及在Python中的程序实现,强调了LU分解在求解线性方程组中的应用。
本文深入讲解了数值分析中的LU分解法,介绍了其基本原理、解题步骤及在Python中的程序实现,强调了LU分解在求解线性方程组中的应用。


















 2万+
2万+












