✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
多式联运是指在不同运输方式之间进行协调与整合,实现货物的高效、快速、安全地运输。在实际应用中,陆海空三种运输方式往往需要相互衔接,才能满足物流需求。然而,由于运输方式的差异性和复杂性,多式联运问题的解决一直是一个难点。
为了解决这个问题,本文提出了一种基于粒子群结合遗传算法求解带时间窗的陆海空多式联运问题算法流程。该算法流程结合了粒子群算法和遗传算法的优点,可以求解带时间窗的多式联运问题,同时兼顾了效率和准确性。
具体而言,该算法流程主要包括以下几个步骤:
1.问题建模
首先,需要将多式联运问题转化为数学模型。在这个模型中,需要考虑货物的需求量、运输方式、时间窗等因素。通过建立合理的数学模型,可以更加准确地描述多式联运问题,并为后续的算法求解提供基础。
2.粒子群算法
接下来,使用粒子群算法进行求解。粒子群算法是一种基于群体智能的优化算法,通过模拟鸟群或鱼群的行为,寻找最优解。在多式联运问题中,可以将货物看作是粒子,通过调整粒子的位置和速度,寻找最优的运输方案。
3.遗传算法
为了进一步提高求解效率和准确性,可以使用遗传算法对粒子群算法的结果进行优化。遗传算法是一种基于遗传学原理的优化算法,通过模拟自然界的进化过程,寻找最优解。在多式联运问题中,可以将运输方案看作是个体,通过交叉、变异等操作,不断优化运输方案,直到达到最优解。
4.算法优化
最后,对算法进行优化。通过调整算法参数、改进算法流程等方式,进一步提高算法的效率和准确性。同时,需要进行大量的实验验证,以确保算法的可行性和有效性。
总之,基于粒子群结合遗传算法求解带时间窗的陆海空多式联运问题算法流程,是一种有效的求解方法。该算法流程不仅可以满足多式联运问题的需求,还可以为相关领域的研究提供参考。在未来的研究中,可以进一步探索算法的优化和应用,为多式联运问题的解决提供更好的方法。
📣 部分代码
%% 画出最优配送方案路线图
%输入:VC 配送方案
%输入:vertexs 各个点的经度和纬度
function draw_Best(VC,vertexs,PD)
customer=vertexs(2:end,:); %门店经度和纬度
NV=size(VC,1); %车辆使用数目
figure
hold on;box on
title('最优多式联运方案路线图')
hold on;
C=hsv(NV);
for i=2:size(vertexs,1)
text(vertexs(i,1)+0.05,vertexs(i,2)+0.05,num2str(i-1),'color',[1,0,0]);
end
for i=1:NV
part_seq=VC{i}; %每辆车所经过的门店
len=length(part_seq); %每辆车所经过的门店数量
part_seq2=PD{i}; %每次的交通方式
for j=0:len
%当j=0时,车辆从配送中心出发到达该路径上的第一个门店
if j==0
fprintf('%s','配送路线',num2str(i),':');
fprintf('%d->',0);
c1=customer(part_seq(1),:);
plot([vertexs(1,1),c1(1)],[vertexs(1,2),c1(2)],'-','color','k','linewidth',2);
%当j=len时,车辆从该路径上的最后一个门店出发到达配送中心
elseif j==len
fprintf('%d->',part_seq(j));
fprintf('%d',0);
fprintf('\n');
c_len=customer(part_seq(len),:);
% plot([c_len(1),vertexs(1,1)],[c_len(2),vertexs(1,2)],'-','color',C(i,:),'linewidth',1);
switch part_seq2(j)
case 1 %陆路
plot([c_len(1),vertexs(1,1)],[c_len(2),vertexs(1,2)],'-','color','k','linewidth',2);hold on
case 2 %空运路
plot([c_len(1),vertexs(1,1)],[c_len(2),vertexs(1,2)],'-','color','g','linewidth',2);hold on
case 3 %水路
plot([c_len(1),vertexs(1,1)],[c_len(2),vertexs(1,2)],'-','color','b','linewidth',2);hold on
end
%否则,车辆从路径上的前一个门店到达该路径上紧邻的下一个门店
else
fprintf('%d->',part_seq(j));
c_pre=customer(part_seq(j),:);
c_lastone=customer(part_seq(j+1),:);
% plot([c_pre(1),c_lastone(1)],[c_pre(2),c_lastone(2)],'-','color',C(i,:),'linewidth',1);
switch part_seq2(j)
case 1 %陆路
plot([c_pre(1),c_lastone(1)],[c_pre(2),c_lastone(2)],'-','color','k','linewidth',2);hold on
case 2 %空运路
plot([c_pre(1),c_lastone(1)],[c_pre(2),c_lastone(2)],'-','color','g','linewidth',2);hold on
case 3 %水路
plot([c_pre(1),c_lastone(1)],[c_pre(2),c_lastone(2)],'-','color','b','linewidth',2);hold on
end
end
end
end
plot(customer(:,1),customer(:,2),'k.','linewidth',1);hold on;
plot(vertexs(1,1),vertexs(1,2),'s','linewidth',2,'MarkerEdgeColor','b','MarkerFaceColor','b','MarkerSize',10);
for i=1:NV
part_seq=PD{i}; %每辆车所经过的门店
len=length(part_seq); %每辆车所经过的门店数量
for j=0:len
if j==0
fprintf('%s','选择方式:');
fprintf('%d');
elseif j==len
fprintf('%d->',part_seq(j));
fprintf('%d');
fprintf('\n');
else
fprintf('%d->',part_seq(j));
end
end
end
⛳️ 运行结果
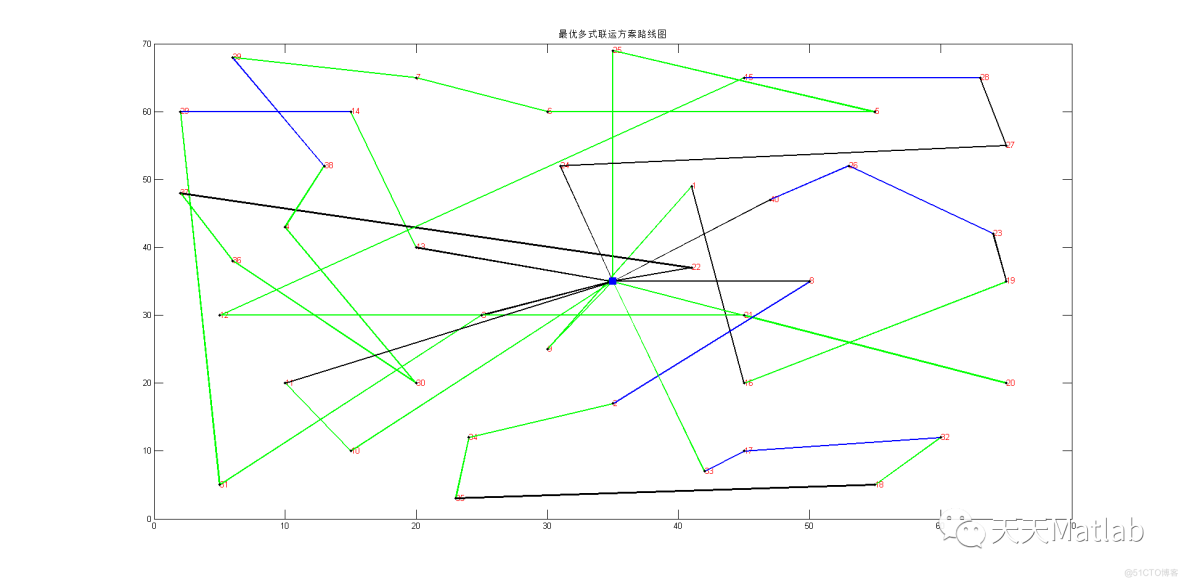




 文章介绍了如何使用粒子群和遗传算法解决陆海空多式联运中的时间窗问题,通过数学模型构建和优化算法流程,以提高运输效率和准确性。算法包括问题建模、粒子群求解、遗传优化和算法优化等步骤,并提供了部分代码示例和运行结果。
文章介绍了如何使用粒子群和遗传算法解决陆海空多式联运中的时间窗问题,通过数学模型构建和优化算法流程,以提高运输效率和准确性。算法包括问题建模、粒子群求解、遗传优化和算法优化等步骤,并提供了部分代码示例和运行结果。
















 450
450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








